Długość każdego boku kwadratu zwiększono o 20%. Wtedy pole tego kwadratu:
A) wzrośnie o 20% B) wzrośnie o 40% C) wzrośnie o 44% D) wzrośnie dwukrotnie
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Czworokąt/Kwadrat
Długość boku kwadratu 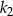 jest o 10% większa od długości boku kwadratu
jest o 10% większa od długości boku kwadratu 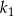 . Wówczas pole kwadratu
. Wówczas pole kwadratu 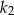 jest większe od pola kwadratu
jest większe od pola kwadratu 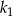 o
o
A) 10% B) 110% C) 21% D) 121%
Z przeciwległych wierzchołków kwadratu o boku 1 zatoczono koła o promieniu 1. Pole części wspólnej tych kół jest równe
A) 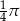 B)
B) 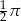 C)
C) 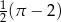 D)
D) 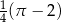
Z przeciwległych wierzchołków kwadratu o boku 2 zatoczono koła o promieniu 2. Pole części wspólnej tych kół jest równe
A) 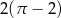 B)
B) 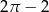 C)
C) 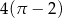 D)
D) 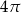
Przekątna kwadratu jest o 2 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 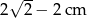 B)
B) 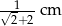 C)
C) 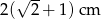 D)
D) 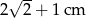
Przekątna kwadratu jest o 4 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 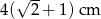 B)
B) 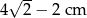 C)
C) 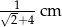 D)
D) 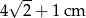
Przekątna kwadratu jest o 3 cm dłuższa od długości boku tego kwadratu. Zatem długość boku kwadratu wynosi
A) 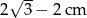 B)
B) 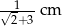 C)
C) 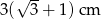 D)
D) 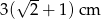
Obwód kwadratu wpisanego w okrąg o długości 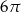 jest równy
jest równy
A) 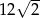 B)
B) 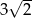 C)
C) 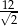 D)
D) 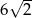
W kwadracie 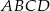 punkt
punkt 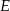 jest środkiem boku
jest środkiem boku 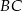 ,
, 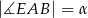 . Wynika stąd, że
. Wynika stąd, że
A) 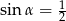 B)
B) 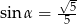 C)
C) 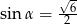 D)
D) 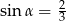
W kwadracie 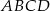 punkt
punkt 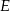 jest środkiem boku
jest środkiem boku 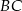 ,
, 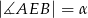 . Wynika stąd, że
. Wynika stąd, że
A) 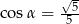 B)
B) 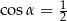 C)
C) 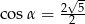 D)
D) 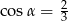
W kwadracie 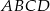 punkt
punkt 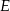 jest środkiem boku
jest środkiem boku 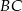 ,
, 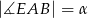 . Wynika stąd, że
. Wynika stąd, że
A) 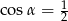 B)
B) 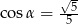 C)
C) 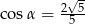 D)
D) 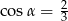
Dany jest kwadrat 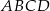 o boku długości 8. Z wierzchołka
o boku długości 8. Z wierzchołka 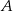 zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
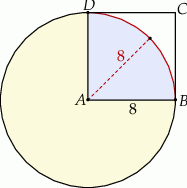
Pole powierzchni części wspólnej koła i kwadratu jest równe
A) 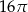 B)
B) 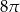 C)
C) 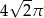 D)
D) 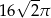
W kwadrat wpisano okrąg o promieniu 6 cm. Obwód tego kwadratu jest równy:
A) 12 cm B) 24 cm C) 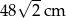 D) 48 cm
D) 48 cm
Prosta przechodząca przez środek 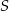 kwadratu
kwadratu 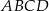 przecina proste zawierające jego boki
przecina proste zawierające jego boki 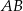 i
i 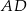 odpowiednio w punktach
odpowiednio w punktach 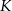 i
i 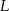 (zobacz rysunek).
(zobacz rysunek).
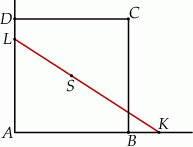
Jeżeli bok kwadratu ma długość 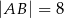 i
i 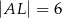 , to pole trójkąta
, to pole trójkąta 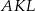 jest równe
jest równe
A) 32 B) 36 C) 40 D) 52
Pole kwadratu 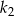 jest o 21% większe od pola kwadratu
jest o 21% większe od pola kwadratu 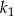 . Wówczas długość boku kwadratu
. Wówczas długość boku kwadratu 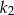 jest większa od długości boku kwadratu
jest większa od długości boku kwadratu 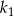 o
o
A) 10% B) 110% C) 21% D) 121%
Przekątna kwadratu 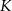 ma długość 2, a obwód kwadratu
ma długość 2, a obwód kwadratu 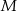 ma długość 16. Skala podobieństwa kwadratu
ma długość 16. Skala podobieństwa kwadratu 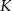 do kwadratu
do kwadratu 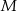 jest równa:
jest równa:
A) 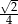 B)
B) 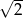 C) 4 D)
C) 4 D) 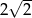
Kwadrat i trójkąt równoboczny mają równe pola. Stosunek długości boku kwadratu do długości boku trójkąta równobocznego jest wtedy równy
A) 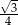 B)
B) 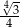 C)
C) 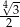 D)
D) 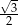
Kwadrat i trójkąt równoboczny mają równe pola. Stosunek długości boku trójkąta równobocznego do długości boku kwadratu jest wtedy równy
A) 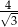 B)
B) 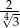 C)
C) 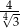 D)
D) 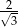
Kwadrat jest wpisany w okrąg o średnicy 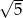 . Bok kwadratu jest równy
. Bok kwadratu jest równy
A) 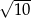 B)
B) 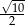 C)
C) 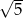 D)
D) 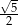
Kwadrat jest wpisany w okrąg o średnicy 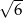 . Bok kwadratu jest równy
. Bok kwadratu jest równy
A) 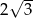 B)
B) 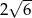 C)
C) 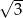 D) 3
D) 3
Okrąg opisany na kwadracie ma promień 8. Długość boku tego kwadratu jest równa
A) 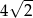 B)
B) 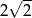 C)
C) 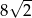 D) 8
D) 8
Kwadrat jest wpisany w okrąg o średnicy 4. Bok kwadratu jest równy
A) 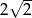 B)
B) 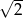 C)
C) 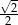 D)
D) 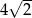
Okrąg opisany na kwadracie ma promień 6. Długość boku tego kwadratu jest równa
A) 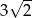 B)
B) 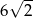 C) 12 D) 6
C) 12 D) 6
Okrąg opisany na kwadracie ma promień 4. Długość boku tego kwadratu jest równa
A) 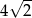 B)
B) 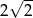 C) 8 D) 4
C) 8 D) 4
W kwadracie 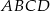 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat 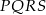 .
.
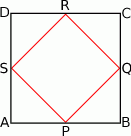
Kwadrat 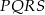 jest podobny do kwadratu
jest podobny do kwadratu 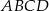 w skali
w skali
A) 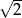 B) 2 C)
B) 2 C) 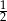 D)
D) 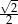
W kwadracie 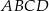 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat 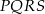 .
.
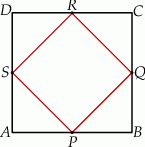
Kwadrat 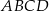 jest podobny do kwadratu
jest podobny do kwadratu 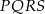 w skali
w skali
A) 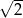 B) 2 C)
B) 2 C) 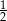 D)
D) 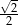
Na boku 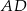 kwadratu
kwadratu 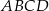 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 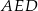 . Punkt
. Punkt 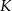 jest środkiem odcinka
jest środkiem odcinka 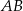 , a punkt
, a punkt 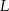 środkiem odcinka
środkiem odcinka 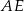 .
.
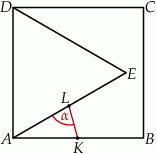
Miara kąta  jest równa
jest równa
A) 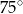 B)
B) 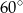 C)
C) 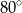 D)
D) 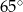
Stosunek pól kół wpisanego i opisanego na kwadracie o boku długości  jest równy:
jest równy:
A) 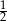 B)
B) 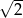 C)
C) 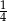 D)
D) 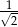
Stosunek pola koła wpisanego w kwadrat do pola koła opisanego na tym kwadracie jest równy:
A) 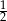 B)
B) 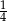 C)
C) 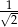 D)
D) 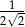
Stosunek pola kwadratu wpisanego w okrąg do pola kwadratu opisanego na tym okręgu wynosi
A) 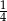 B)
B) 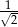 C)
C) 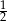 D)
D) 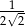
Długość jednego boku kwadratu 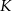 skrócono o 20%, a długość drugiego boku skrócono o 40%. W wyniku tych operacji otrzymano prostokąt
skrócono o 20%, a długość drugiego boku skrócono o 40%. W wyniku tych operacji otrzymano prostokąt 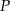 . Stosunek długości przekątnej kwadratu
. Stosunek długości przekątnej kwadratu 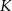 do długości przekątnej prostokąta
do długości przekątnej prostokąta 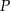 jest równy
jest równy
A) 0,48 B) 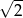 C) 1 D) 2
C) 1 D) 2
Pole kwadratu wpisanego w okrąg o promieniu 4 cm jest równe
A) 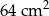 B)
B) 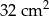 C)
C) 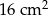 D)
D) 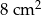
Pole kwadratu wpisanego w okrąg o średnicy 10 jest równe
A) 100 B) 75 C) 50 D) 25
Pole kwadratu wpisanego w okrąg o promieniu 5 jest równe
A) 25 B) 50 C) 75 D) 100
Pole kwadratu wpisanego w okrąg o promieniu 6 cm jest równe
A) 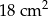 B)
B) 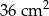 C)
C) 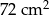 D)
D) 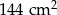
Na boku 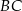 kwadratu
kwadratu 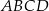 (na zewnątrz) zbudowano trójkąt równoboczny
(na zewnątrz) zbudowano trójkąt równoboczny 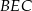 (zobacz rysunek).
(zobacz rysunek).
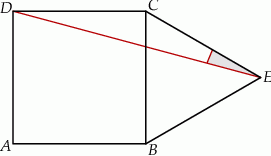
Miara kąta 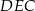 jest równa
jest równa
A) 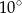 B)
B) 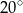 C)
C) 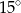 D)
D) 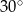
Dany jest kwadrat o przekątnej 6. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 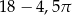 B)
B) 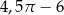 C)
C) 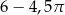 D)
D) 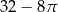
Dany jest kwadrat o przekątnej 2. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 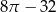 B)
B) 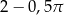 C)
C) 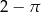 D)
D) 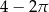
Dany jest kwadrat o przekątnej 4. Z wierzchołka kwadratu zatoczono koło o promieniu równym długości boku kwadratu. Pole figury będącej różnicą kwadratu i koła jest równe
A) 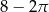 B)
B) 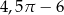 C)
C) 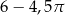 D)
D) 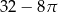
W kwadracie 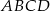 o boku długości 20 połączono punkty
o boku długości 20 połączono punkty 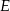 i
i 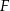 na bokach
na bokach 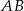 i
i 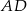 w ten sposób, że odcinek
w ten sposób, że odcinek 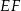 jest równoległy do przekątnej
jest równoległy do przekątnej 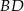 i jest od niej 5 razy krótszy.
i jest od niej 5 razy krótszy.
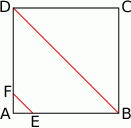
Długość odcinka 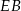 jest równa
jest równa
A) 12 B) 15 C) 14 D) 16

