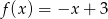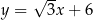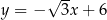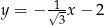Wszystkich liczb naturalnych pięciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry 0, 5, 7, jest
A) 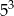 B)
B) 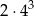 C)
C) 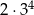 D)
D) 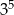
/Szkoła średnia
Kąt  jest ostry i
jest ostry i 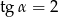 . Oblicz
. Oblicz 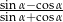 .
.
Funkcja kwadratowa 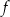 jest określona wzorem
jest określona wzorem 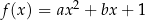 , gdzie
, gdzie  oraz
oraz 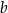 są pewnymi liczbami rzeczywistymi, takimi, że
są pewnymi liczbami rzeczywistymi, takimi, że 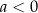 i
i 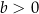 . Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych
. Na jednym z rysunków A–D przedstawiono fragment wykresu tej funkcji w kartezjańskim układzie współrzędnych 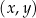 . Fragment wykresu funkcji
. Fragment wykresu funkcji 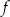 przedstawiono na rysunku
przedstawiono na rysunku
Trzywyrazowy ciąg  jest geometryczny. Dokończ zdanie tak, aby było prawdziwe. Ciąg
jest geometryczny. Dokończ zdanie tak, aby było prawdziwe. Ciąg  jest
jest
| A) rosnący, | B) malejący |
oraz
1) 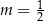 , , | 2) 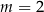 , , | 3) 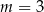 , , |
Rysunek przedstawia fragment wykresu funkcji 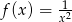 .
.
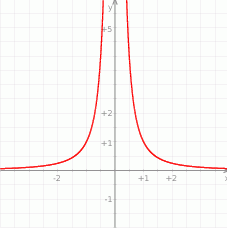
Przeprowadzono prostą równoległą do osi  , która przecięła wykres tej funkcji w punktach
, która przecięła wykres tej funkcji w punktach  i
i  . Niech
. Niech 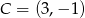 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 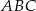 jest większe lub równe 2.
jest większe lub równe 2.
Trapez równoramienny 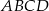 o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa 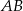 trapezu, o długości 12, jest średnicą tego okręgu. Przekątne
trapezu, o długości 12, jest średnicą tego okręgu. Przekątne 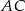 i
i 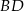 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 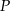 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 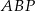 .
.
Kąt  jest ostry i
jest ostry i 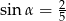 . Wówczas
. Wówczas 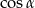 jest równy
jest równy
A)  B)
B) 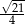 C)
C)  D)
D) 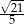
Rozwiązaniem równania 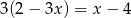 jest:
jest:
A) 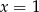 B)
B) 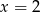 C)
C) 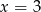 D)
D) 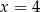
Funkcja 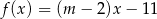 jest rosnąca, gdy
jest rosnąca, gdy
A) 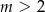 B)
B) 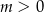 C)
C) 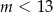 D)
D) 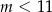
Wszystkie wyrazy ciągu geometrycznego 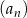 , określonego dla
, określonego dla 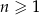 , są liczbami dodatnimi. Drugi wyraz tego ciągu jest równy 162, a piąty wyraz jest równy 48. Oznacza to, że iloraz tego ciągu jest równy
, są liczbami dodatnimi. Drugi wyraz tego ciągu jest równy 162, a piąty wyraz jest równy 48. Oznacza to, że iloraz tego ciągu jest równy
A)  B)
B)  C)
C) 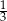 D)
D) 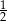
Na rysunku przedstawiono wykres funkcji 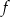 .
.
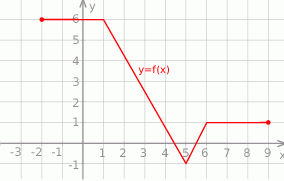
Funkcja 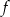 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 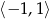 B)
B) 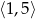 C)
C) 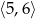 D)
D) 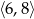
Dane są dwa okręgi: okrąg o środku w punkcie 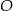 i promieniu 5 oraz okrąg o środku w punkcie
i promieniu 5 oraz okrąg o środku w punkcie 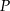 i promieniu 3. Odcinek
i promieniu 3. Odcinek 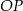 ma długość 16. Prosta
ma długość 16. Prosta 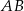 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach 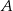 i
i 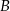 . Ponadto prosta
. Ponadto prosta 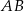 przecina odcinek
przecina odcinek 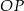 w punkcie
w punkcie 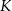 (zobacz rysunek).
(zobacz rysunek).
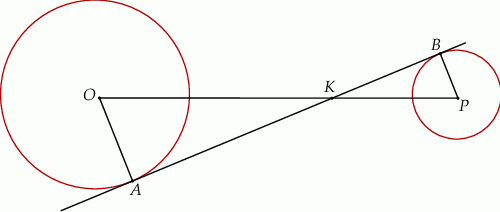
Wtedy
A) 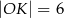 B)
B) 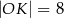 C)
C) 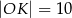 D)
D) 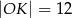
Dany jest ciąg geometryczny 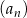 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 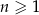 . Drugi wyraz tego ciągu oraz iloraz ciągu
. Drugi wyraz tego ciągu oraz iloraz ciągu 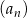 są równe 2. Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa
są równe 2. Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 1 B) 11 C) 21 D) 31
Rozwiąż równanie 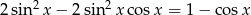 w przedziale
w przedziale 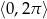 .
.
W kartezjańskim układzie współrzędnych 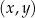 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami trójkąta 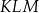 . Trójkąt
. Trójkąt 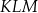 jest
jest
| A) równoramienny, | B) prostokątny, |
ponieważ
| 1) | oś 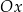 przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. przechodzi przez jeden z wierzchołków tego trójkąta i środek jednego z boków tego trójkąta. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | oś 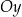 zawiera dwusieczną tego trójkąta. zawiera dwusieczną tego trójkąta. |
Liczba 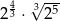 jest równa
jest równa
A) 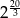 B) 2 C)
B) 2 C) 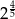 D)
D) 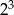
Iloczyn liczb spełniających równanie 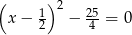 jest równy
jest równy
A) 6 B) 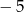 C) 5 D)
C) 5 D) 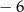
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy
, jaki przekątna tego graniastosłupa tworzy z jego podstawą, jest równy 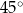 (zobacz rysunek).
(zobacz rysunek).
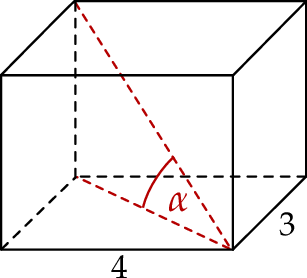
Wysokość graniastosłupa jest równa
A) 5 B) 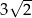 C)
C) 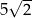 D)
D) 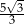
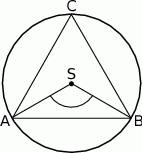
Punkty 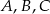 leżące na okręgu o środku
leżące na okręgu o środku 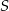 są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego
są wierzchołkami trójkąta równobocznego. Miara zaznaczonego na rysunku kąta środkowego 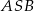 jest równa
jest równa
A) 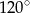 B)
B) 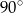 C)
C) 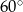 D)
D) 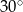
Do wykresu funkcji liniowej 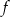 należą punkty
należą punkty 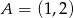 i
i 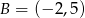 . Funkcja
. Funkcja 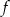 ma wzór
ma wzór
A) 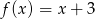 B)
B) 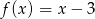 C)
C) 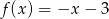 D)
D)