Liczba 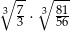 jest równa
jest równa
A) 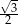 B)
B) 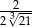 C)
C)  D)
D) 
/Szkoła średnia
Podstawą ostrosłupa 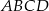 jest trójkąt równoramienny o podstawie
jest trójkąt równoramienny o podstawie 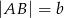 i kącie
i kącie  pomiędzy ramionami. Krawędź
pomiędzy ramionami. Krawędź 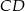 jest wysokością ostrosłupa, a kąt nachylenia ściany
jest wysokością ostrosłupa, a kąt nachylenia ściany 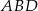 do podstawy ostrosłupa jest równy
do podstawy ostrosłupa jest równy 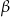 . Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Funkcja kwadratowa jest określona wzorem 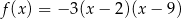 . Liczby
. Liczby  są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji  . Zatem
. Zatem
A) 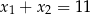 B)
B) 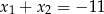 C)
C) 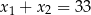 D)
D) 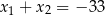
Para liczb 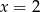 i
i 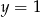 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań 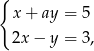 gdy
gdy
A) 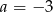 B)
B) 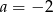 C)
C) 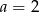 D)
D) 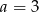
W trójkącie 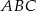 punkt
punkt 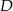 leży na boku
leży na boku 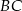 , a punkt
, a punkt 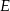 leży na boku
leży na boku 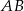 . Odcinek
. Odcinek 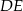 jest równoległy do boku
jest równoległy do boku 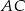 , a ponadto
, a ponadto  ,
, 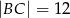 i
i 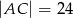 (zobacz rysunek).
(zobacz rysunek).
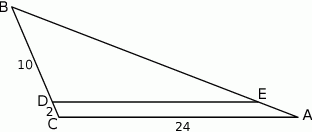
Długość odcinka 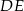 jest równa
jest równa
A) 22 B) 20 C) 12 D) 11
Liczba 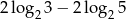 jest równa
jest równa
A) 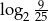 B)
B) 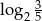 C)
C) 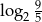 D)
D) 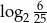
Wartość wyrażenia 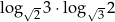 jest równa
jest równa
A)  B)
B) 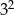 C)
C) 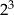 D) 4
D) 4
W kartezjańskim układzie współrzędnych  prosta
prosta 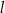 o równaniu
o równaniu 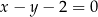 przecina parabolę o równaniu
przecina parabolę o równaniu 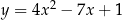 w punktach
w punktach  oraz
oraz  . Odcinek
. Odcinek  jest średnicą okręgu
jest średnicą okręgu 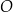 . Punkt
. Punkt 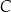 leży na okręgu
leży na okręgu 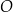 nad prostą
nad prostą 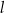 , a kąt
, a kąt 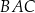 jest ostry i ma miarę
jest ostry i ma miarę  taką, że
taką, że 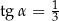 (zobacz rysunek).
(zobacz rysunek).
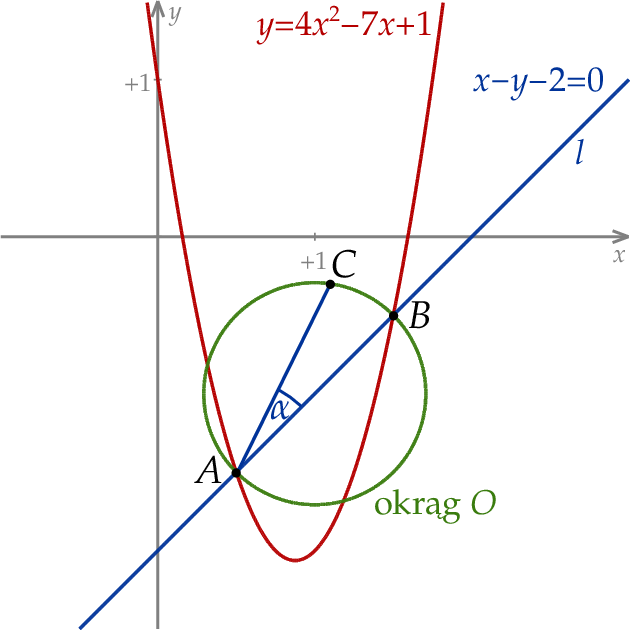
Oblicz współrzędne punktu 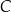 .
.
Funkcja 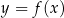 jest określona za pomocą tabeli
jest określona za pomocą tabeli
 | 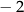 | 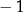 | 0 | 1 | 2 |
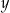 | 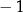 | 0 | 1 | 0 | 3 |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 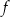 ma dokładnie jedno miejsce zerowe. ma dokładnie jedno miejsce zerowe. | P | F |
Wykres funkcji 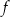 jest symetryczny względem osi jest symetryczny względem osi 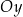 . . | P | F |
Wszystkich liczb naturalnych czterocyfrowych parzystych, w których występują wyłącznie cyfry 1, 2, 3, jest
A) 54 B) 81 C) 8 D) 27
Rozwiąż równanie 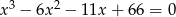 .
.
Suma długości dwóch boków trójkąta równa się 4, a kąt między tymi bokami ma miarę 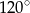 . Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta.
. Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta.
W kartezjańskim układzie współrzędnych 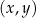 przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej
przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej 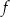 (zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
(zobacz rysunek). Wierzchołek tej paraboli oraz punkty przecięcia paraboli z osiami układu współrzędnych mają obie współrzędne całkowite.
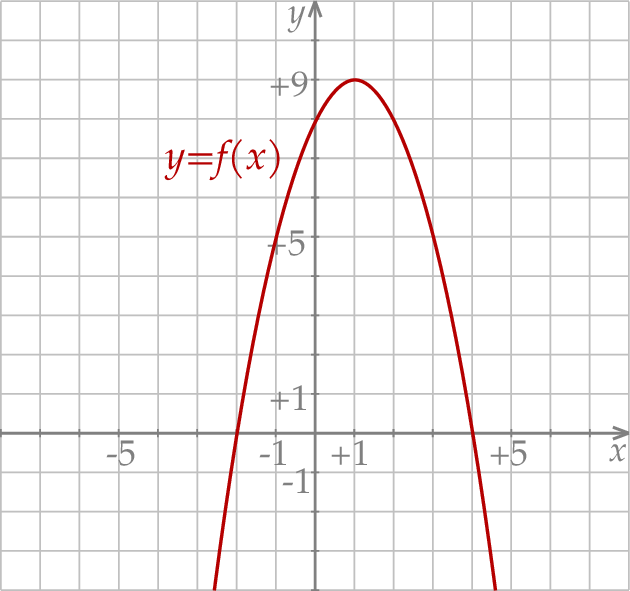
Funkcja kwadratowa 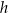 jest określona za pomocą funkcji
jest określona za pomocą funkcji 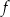 następująco:
następująco: 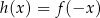 . Fragment wykresu funkcji
. Fragment wykresu funkcji 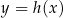 przedstawiono na rysunku
przedstawiono na rysunku
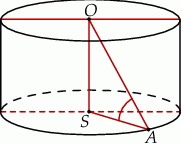
Promień  podstawy walca jest równy wysokości
podstawy walca jest równy wysokości  tego walca. Sinus kąta
tego walca. Sinus kąta 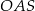 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 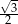 B)
B) 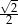 C)
C) 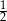 D) 1
D) 1
W trójkącie prostokątnym o długościach przyprostokątnych 2 i 5 cosinus większego z kątów ostrych jest równy
A)  B)
B)  C)
C) 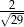 D)
D) 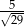
Funkcja 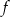 określona jest wzorem
określona jest wzorem 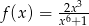 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wtedy liczba
. Wtedy liczba 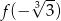 jest równa
jest równa
A) 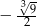 B)
B) 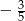 C)
C)  D)
D) 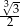
Punkty 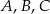 i
i 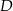 leżą na okręgu o środku
leżą na okręgu o środku 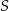 . Miary kątów
. Miary kątów 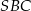 ,
, 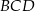 ,
, 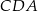 są równe odpowiednio:
są równe odpowiednio: 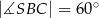 ,
, 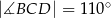 ,
, 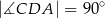 (zobacz rysunek).
(zobacz rysunek).
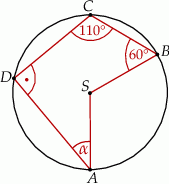
Wynika stąd, że miara  kąta
kąta 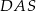 jest równa
jest równa
A) 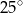 B)
B) 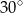 C)
C) 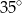 D)
D) 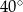
Wielomian 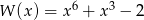 jest równy iloczynowi
jest równy iloczynowi
A) 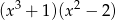 B)
B) 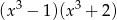 C)
C) 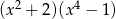 D)
D) 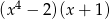
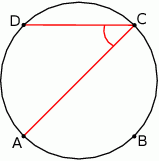
Punkty 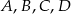 dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego 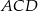 jest równa
jest równa
A) 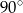 B)
B) 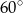 C)
C) 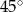 D)
D) 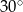
Dana jest funkcja 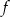 określona wzorem
określona wzorem 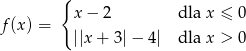
Równanie 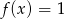 ma dokładnie
ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) cztery rozwiązania. D) pięć rozwiązań.

