Promień kuli o objętości 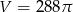 jest równy
jest równy
A) 18 B) 9 C) 8 D) 6
/Szkoła średnia
Wierzchołkiem paraboli będącej wykresem funkcji określonej wzorem 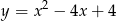 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 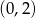 B)
B) 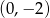 C)
C) 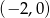 D)
D) 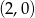
Funkcja 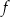 jest określona wzorem
jest określona wzorem
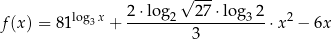
dla każdej liczby dodatniej  .
.
-
Wykaż, że dla każdej liczby dodatniej
 wzór funkcji
wzór funkcji 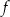 można równoważnie przekształcić do postaci
można równoważnie przekształcić do postaci 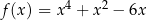 .
. -
Oblicz najmniejszą wartość funkcji
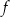 określonej dla każdej liczby dodatniej
określonej dla każdej liczby dodatniej  .
.
Na rysunku, w kartezjańskim układzie współrzędnych 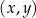 , przedstawiono interpretację geometryczną jednego z poniższych układów równań
, przedstawiono interpretację geometryczną jednego z poniższych układów równań
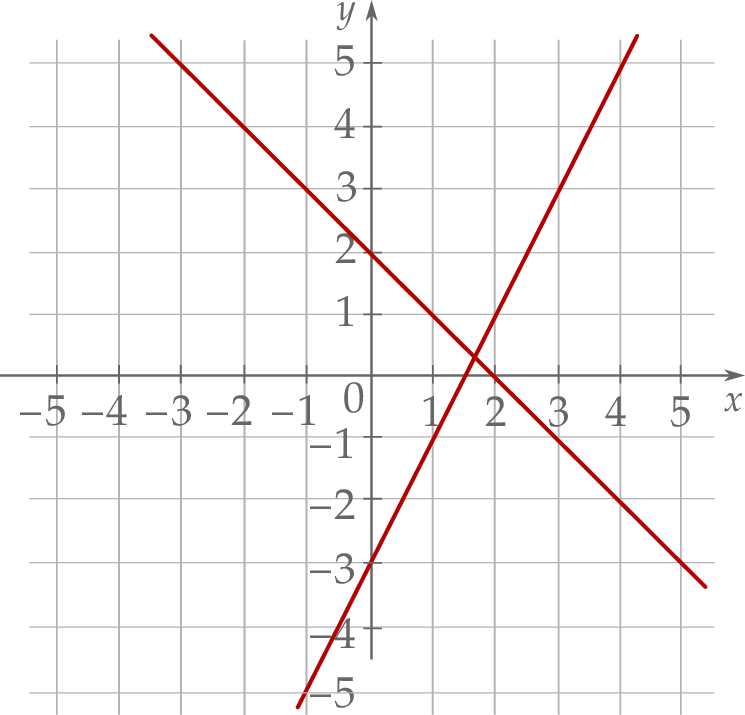
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 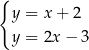 B)
B) 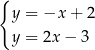 C)
C) 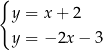 D)
D) 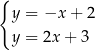
Korzystając z danych przedstawionych na rysunku, oblicz wartość wyrażenia:
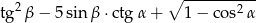
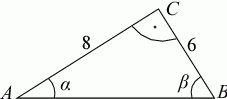
Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
A) 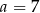 B)
B) 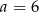 C)
C) 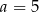 D)
D) 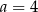
Przez punkty 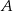 i
i 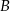 , leżące na okręgu o środku
, leżące na okręgu o środku 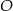 , poprowadzono proste styczne do tego okręgu, przecinające się w punkcie
, poprowadzono proste styczne do tego okręgu, przecinające się w punkcie 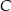 (zobacz rysunek).
(zobacz rysunek).
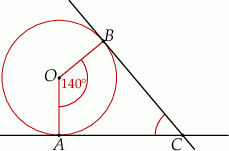
Miara kąta 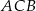 jest równa
jest równa
A) 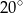 B)
B) 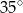 C)
C) 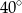 D)
D) 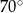
Jeżeli ostrosłup ma 10 krawędzi, to liczba ścian bocznych jest równa
A) 5 B) 7 C) 8 D) 10
Różnica 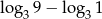 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Prosta przechodząca przez punkty 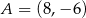 i
i 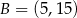 jest styczna do okręgu o środku w punkcie
jest styczna do okręgu o środku w punkcie 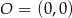 . Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą
. Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą 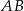 .
.
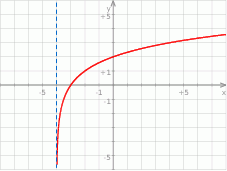
Na rysunku przedstawiony jest fragment wykresu funkcji logarytmicznej 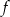 określonej wzorem
określonej wzorem 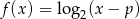 .
.
- Podaj wartość
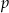 .
. - Narysuj wykres funkcji określonej wzorem
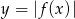 .
. - Podaj wszystkie wartości parametru
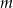 , dla których równanie
, dla których równanie 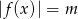 ma dwa rozwiązania o przeciwnych znakach.
ma dwa rozwiązania o przeciwnych znakach.
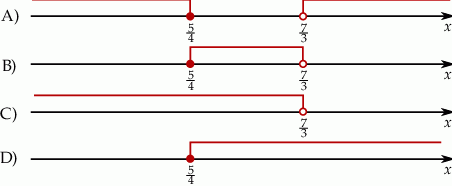
Wskaż rysunek, na którym przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających jednocześnie nierówności 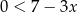 oraz
oraz 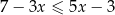 .
.
Średnia arytmetyczna sześciu liczb: 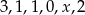 jest równa 2. Wtedy liczba
jest równa 2. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Objętość sześcianu jest równa 64. Pole powierzchni całkowitej tego sześcianu jest równe
A) 512 B) 384 C) 96 D) 16
Wyznacz równanie okręgu przechodzącego przez punkty 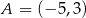 i
i 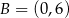 , którego środek leży na prostej o równaniu
, którego środek leży na prostej o równaniu 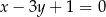 .
.
Ze zbioru dziewięcioelementowego 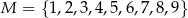 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 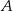 polega na wylosowaniu dwóch liczb ze zbioru
polega na wylosowaniu dwóch liczb ze zbioru 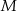 , których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia
, których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia 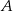 .
.
Rejsowy samolot z Warszawy do Rzymu przelatuje nad Austrią każdorazowo tą samą trasą z taką samą zakładaną prędkością przelotową. We wtorek jego średnia prędkość była o 10% większa niż prędkość przelotowa, a w czwartek średnia prędkość była o 10% mniejsza od zakładanej prędkości przelotowej. Czas przelotu nad Austrią w czwartek różnił się od wtorkowego o 12 minut. Jak długo trwał przelot tego samolotu nad Austrią we wtorek?
O ciągu 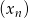 dla
dla 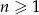 wiadomo, że:
wiadomo, że:
- ciąg
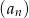 określony wzorem
określony wzorem 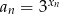 dla
dla 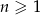 jest geometryczny o ilorazie
jest geometryczny o ilorazie 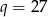 .
. 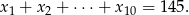
Oblicz 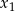 .
.
Układ równań 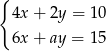 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 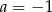 B)
B) 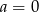 C)
C) 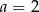 D)
D) 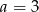
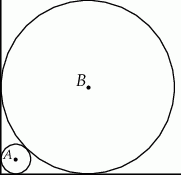
Dwa okręgi o środkach 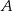 i
i 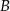 są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia większego z tych okręgów do promienia mniejszego jest równy
są styczne zewnętrznie i każdy z nich jest jednocześnie styczny do ramion tego samego kąta prostego. Udowodnij, że stosunek promienia większego z tych okręgów do promienia mniejszego jest równy 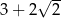 .
.