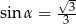Liczba przekątnych sześcianu to
A) 6 B) 12 C) 8 D) 4
/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Sześcian/Inne
Suma długości wszystkich krawędzi i wszystkich przekątnych ścian sześcianu jest równa 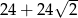 . Jaka jest objętość tego sześcianu?
. Jaka jest objętość tego sześcianu?
A) 8 B) 27 C) 64 D) 96
Suma długości wszystkich krawędzi sześcianu jest o 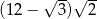 większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
A) 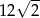 B) 12 C) 2 D)
B) 12 C) 2 D) 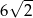
Dany jest sześcian 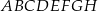 . Przekątne
. Przekątne 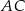 i
i 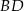 ściany
ściany 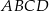 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 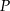 (zobacz rysunek).
(zobacz rysunek).
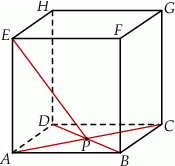
Tangens kąta, jaki odcinek 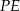 tworzy z płaszczyzną
tworzy z płaszczyzną 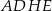 , jest równy
, jest równy
A) 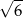 B)
B) 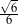 C)
C) 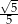 D)
D) 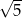
Dany jest sześcian 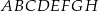 .
.
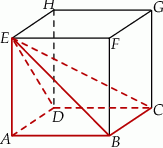
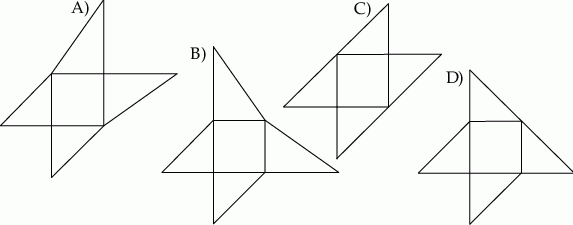
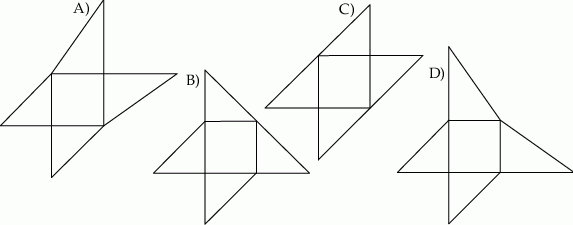
Siatką ostrosłupa czworokątnego 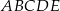 jest
jest
Dany jest sześcian 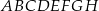 .
.
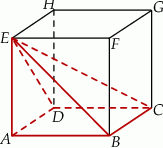
Siatką ostrosłupa czworokątnego 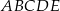 jest
jest
Promień sfery opisanej na sześcianie jest równy 6. Długość krawędzi tego sześcianu jest równa
A) 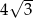 B)
B) 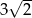 C)
C) 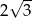 D)
D) 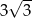
W sześcianie 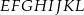 poprowadzono z wierzchołka
poprowadzono z wierzchołka 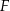 dwie przekątne sąsiednich ścian,
dwie przekątne sąsiednich ścian, 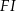 oraz
oraz 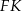 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 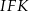 jest równa
jest równa
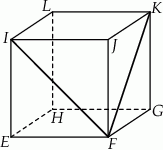
A) 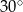 B)
B) 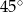 C)
C) 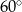 D)
D) 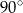
Dany jest sześcian 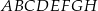 . Przekątne
. Przekątne 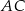 i
i 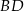 ściany
ściany 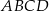 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 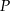 (zobacz rysunek).
(zobacz rysunek).
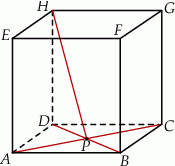
Tangens kąta, jaki odcinek 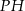 tworzy z płaszczyzną
tworzy z płaszczyzną 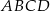 , jest równy
, jest równy
A) 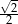 B)
B) 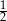 C) 1 D)
C) 1 D) 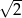
Dany jest sześcian 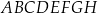 . Przekątne
. Przekątne 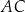 i
i 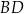 ściany
ściany 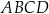 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 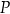 (zobacz rysunek).
(zobacz rysunek).
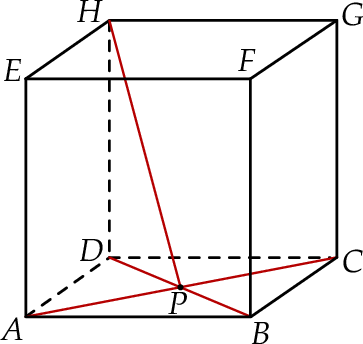
Tangens kąta, jaki odcinek 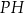 tworzy z krawędzią
tworzy z krawędzią 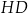 , jest równy
, jest równy
A) 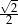 B)
B) 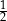 C) 1 D)
C) 1 D) 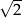
Jeżeli  oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
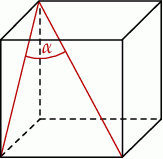
A) 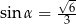 B)
B) 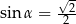 C)
C) 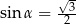 D)
D) 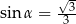
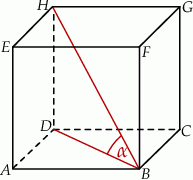
Dany jest sześcian 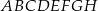 . Sinus kąta
. Sinus kąta  nachylenia przekątnej
nachylenia przekątnej 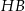 tego sześcianu do płaszczyzny podstawy
tego sześcianu do płaszczyzny podstawy  (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 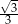 B)
B) 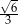 C)
C) 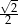 D)
D) 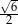
Jeżeli  oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątną sześcianu a przekątną ściany bocznej tego sześcianu (zobacz rysunek), to
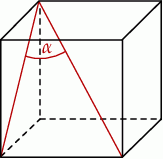
A) 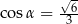 B)
B) 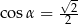 C)
C) 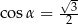 D)
D) 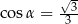
Jeżeli  oznacza miarę kąta między przekątnymi ścian sześcianu (zobacz rysunek), to
oznacza miarę kąta między przekątnymi ścian sześcianu (zobacz rysunek), to
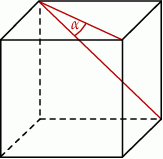
A) 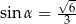 B)
B) 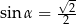 C)
C) 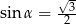 D)
D)