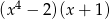Wielomian 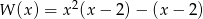 można zapisać w postaci
można zapisać w postaci
A) 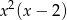 B)
B) 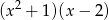 C)
C) 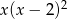 D)
D) 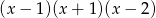
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Jeden wielomian/Przekształcenie wzoru
Wielomian 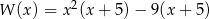 można przedstawić w postaci
można przedstawić w postaci
A) 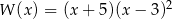 B)
B) 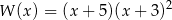
C) 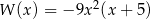 D)
D) 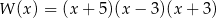
Wielomian 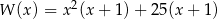 można przedstawić w postaci
można przedstawić w postaci
A) 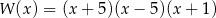 B)
B) 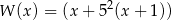
C) 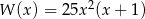 D)
D) 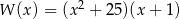
Wielomian 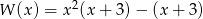 można zapisać w postaci
można zapisać w postaci
A) 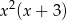 B)
B) 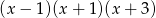 C)
C) 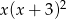 D)
D) 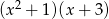
Wielomian 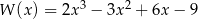 jest podzielny przez wielomian
jest podzielny przez wielomian
A) 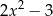 B)
B) 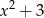 C)
C) 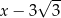 D)
D) 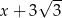
Po rozłożeniu wielomianu 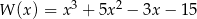 otrzymujemy
otrzymujemy
A) 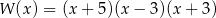 B)
B) 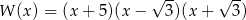
C) 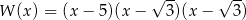 D)
D) 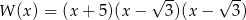
Wielomian 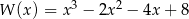 można przedstawić w postaci
można przedstawić w postaci
A) 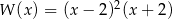 B)
B) 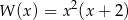
C) 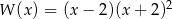 D)
D) 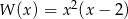
Wielomian 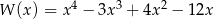 po rozłożeniu na czynniki ma postać:
po rozłożeniu na czynniki ma postać:
A) 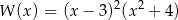 B)
B) 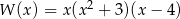
C) 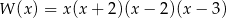 D)
D) 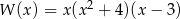
Wielomian 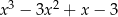 po rozłożeniu na czynniki ma postać:
po rozłożeniu na czynniki ma postać:
A) 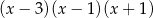 B)
B) 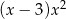
C) 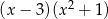 D)
D) 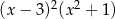
Wielomian 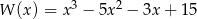 rozłożony na czynniki ma postać
rozłożony na czynniki ma postać
A) 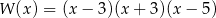 B)
B) 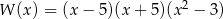
C) 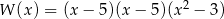 D)
D) 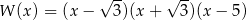
Wielomian 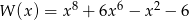 jest równy iloczynowi
jest równy iloczynowi
A) 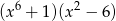 B)
B) 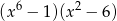 C)
C) 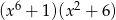 D)
D) 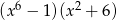
Wielomian 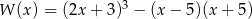 przedstawiony w postaci sumy algebraicznej przyjmuje postać:
przedstawiony w postaci sumy algebraicznej przyjmuje postać:
A) 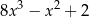 B)
B) 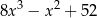
C) 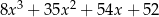 D)
D) 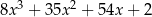
Wielomian 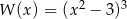 jest równy wielomianowi
jest równy wielomianowi
A) 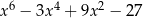 B)
B) 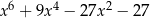
C) 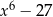 D)
D) 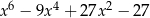
Wielomian 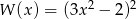 jest równy wielomianowi
jest równy wielomianowi
A) 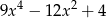 B)
B) 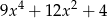 C)
C) 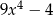 D)
D) 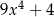
Wielomian 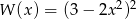 jest równy wielomianowi
jest równy wielomianowi
A) 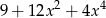 B)
B) 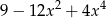 C)
C) 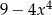 D)
D) 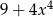
Wielomian 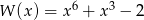 jest równy iloczynowi
jest równy iloczynowi
A) 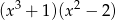 B)
B) 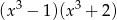 C)
C) 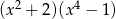 D)
D) 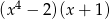
Wielomian 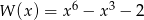 jest równy iloczynowi
jest równy iloczynowi
A) 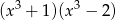 B)
B) 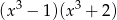 C)
C) 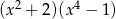 D)
D)