Oblicz objętość i pole powierzchni graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 6 cm i 8 cm, którego przekątna ściany bocznej tworzy z krawędzią podstawy kąt o mierze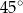 
.
/Szkoła podstawowa/Geometria/Figury przestrzenne/Graniastosłupy
Na rysunku przedstawiono fragment siatki graniastosłupa prawidłowego trójkątnego.
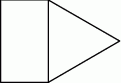
Pole narysowanego trójkąta jest równe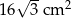 
, a pole prostokąta jest równe 
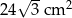. Oblicz objętość tego graniastosłupa.
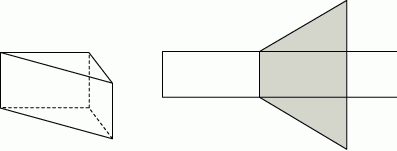
Graniastosłup prawidłowy czworokątny przecięto płaszczyzną, która zawiera krawędź podstawy oraz przechodzi przez środek przeciwległej krawędzi bocznej (zobacz rysunek).
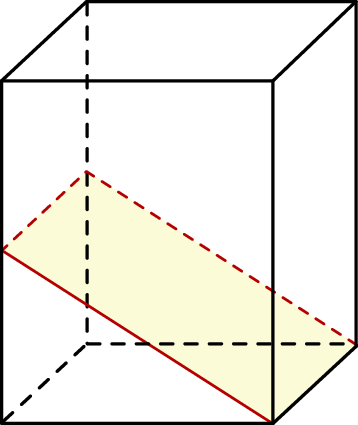
Oblicz jaki jest stosunek objętości dwóch brył na jakie został podzielony ten graniastosłup.
Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest prostokąt.
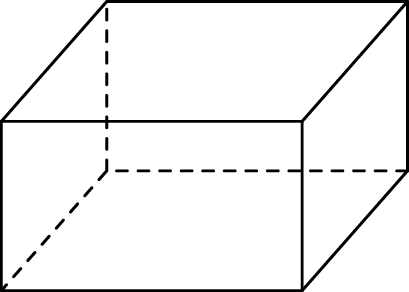
Jeden z boków tego prostokąta ma długość 16 cm, a długość jego przekątnej jest równa 20 cm. Przekątna najmniejszej ściany bocznej graniastosłupa ma długość 15 cm. Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.
Oblicz objętość graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 16 cm i 30 cm, a krawędź boczna jest dwa razy dłuższa od krawędzi podstawy.
Dany jest graniastosłup prawidłowy czworokątny, w którym zaznaczone podstawy są kwadratami. Suma długości jego krawędzi zaznaczonych pogrubioną linią na rysunku 1. jest równa 27 cm. Suma długości jego krawędzi zaznaczonych pogrubioną linią na rysunku 2. jest równa 30 cm.
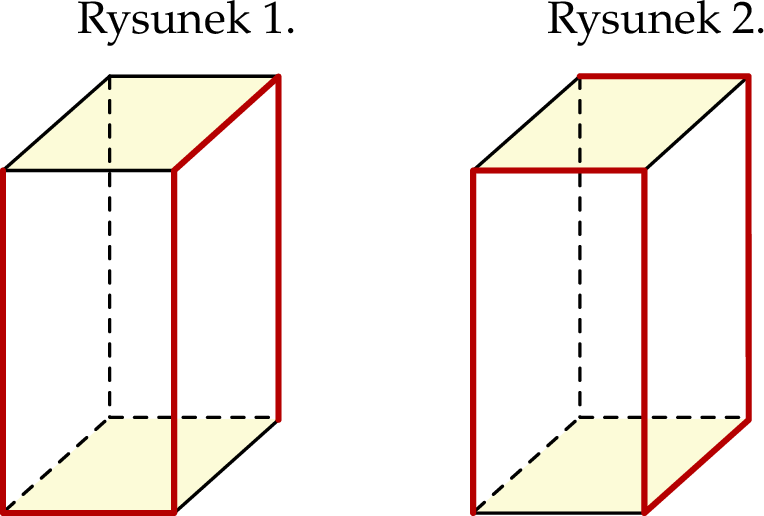
Oblicz objętość tego graniastosłupa.
Z czterech ołowianych sześcianów o przekątnej długości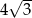 
wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
W graniastosłupie prawidłowym czworokątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu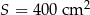 
. Oblicz objętość i pole powierzchni całkowitej tej bryły .
Ukryj
Podobne zadania
W graniastosłupie prawidłowym trójkątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu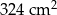 
. Oblicz objętość tej bryły .
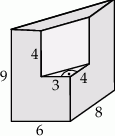
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni tej bryły.
Pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego jest 6 razy większe, od jego pola podstawy, a objętość tego graniastosłupa jest równa 12. Oblicz długość krawędzi podstawy oraz długość przekątnej tego graniastosłupa. Zapisz obliczenia.
Graniastosłup prawidłowy trójkątny o krawędzi podstawy 4 cm i wysokości 10 cm przecięto płaszczyzną zawierającą wysokość podstawy i jedną z krawędzi bocznych. Jakie pole ma ten przekrój?
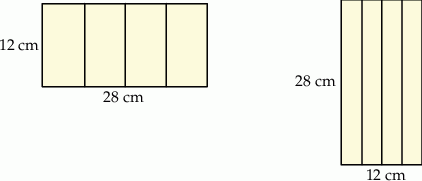
Maja zrobiła dwa pudełka w kształcie graniastosłupów prawidłowych czworokątnych o różnych objętościach. Powierzchnię boczną każdego z tych graniastosłupów wykonała z takich samych prostokątów o wymiarach 28 cm i 12 cm (patrz rysunek). Oblicz różnicę objętości tych graniastosłupów. Zapisz obliczenia.
Ukryj
Podobne zadania
Oskar zrobił dwa pudełka w kształcie graniastosłupów prawidłowych: czworokątnego i sześciokątnego. Powierzchnię boczną każdego z tych graniastosłupów wykonał z takich samych prostokątów o wymiarach 24 cm i 12 cm (patrz rysunek). Oblicz stosunek objętości tych graniastosłupów oraz ustal, który z nich ma większą objętość.
Pole powierzchni bocznej graniastosłupa prawidłowego sześciokątnego jest równe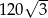 
, a pole jego powierzchni całkowitej wynosi 
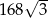. Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia.
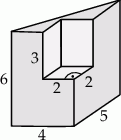
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
Ukryj
Podobne zadania
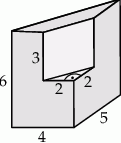
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest trójkąt prostokątny. Długość jednej z przyprostokątnych jest równa 8 cm, a długość przeciwprostokątnej jest równa 10 cm. Najmniejsza ściana boczna tego graniastosłupa ma pole równe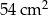 
.
Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.
Ukryj
Podobne zadania
Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest trójkąt prostokątny. Długość jednej z przyprostokątnych jest równa 12 cm, a długość przeciwprostokątnej jest równa 15 cm. Najmniejsza ściana boczna tego graniastosłupa ma pole równe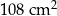 
.
Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.
Na rysunku przedstawiono graniastosłup prosty o podstawie trójkąta prostokątnego i jego siatkę. Dwie dłuższe krawędzie podstawy graniastosłupa mają 12 cm i 13 cm długości, a pole zacieniowanej części siatki graniastosłupa jest równe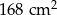 
. Oblicz objętość tego graniastosłupa. Zapisz obliczenia.
Ukryj
Podobne zadania
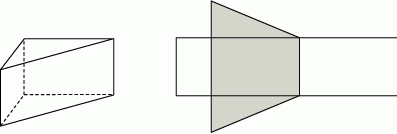
Na rysunku przedstawiono graniastosłup prosty o podstawie trójkąta prostokątnego i jego siatkę. Najkrótsza krawędź podstawy graniastosłupa ma długość 9 cm, a wysokość graniastosłupa ma długość 8 cm. Pole zacieniowanej części siatki graniastosłupa jest równe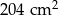 
. Oblicz pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia.
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano niektóre wymiary tej siatki.
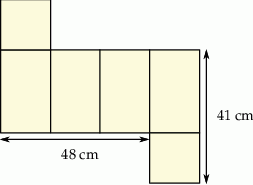
Oblicz objętość tego graniastosłupa.
Ukryj
Podobne zadania
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano niektóre wymiary tej siatki.
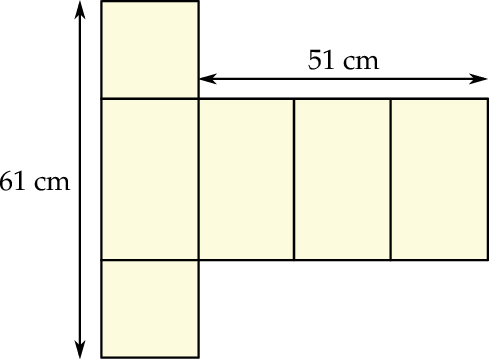
Oblicz objętość tego graniastosłupa.
Na rysunku przedstawiono siatkę graniastosłupa prostego, którego podstawą jest równoległobok. Na rysunku zapisano niektóre wymiary tej siatki.
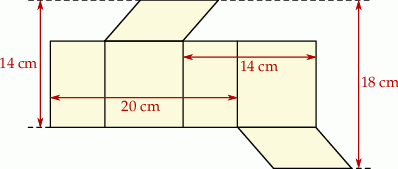
Oblicz objętość tego graniastosłupa.
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe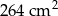 
. Pole podstawy tej bryły stanowi 75% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.
Ukryj
Podobne zadania
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe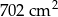 
. Pole podstawy tej bryły stanowi 60% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.
Ile ścian bocznych ma graniastosłup o 14 wierzchołkach?
Ukryj
Podobne zadania
Czy istnieje graniastosłup, który nie ma przekątnych?
Czy graniastosłup może mieć 20 krawędzi?
Czy w każdym graniastosłupie prawidłowym wszystkie przekątne mają tę samą długość?
Czy graniastosłup może mieć 10 ścian bocznych i 20 wierzchołków?
Ile ścian bocznych ma graniastosłup o 100 wierzchołkach?
