Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 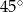 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 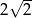 B)
B) 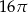 C)
C) 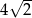 D)
D) 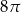
/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Stożek/Różne
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 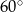 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 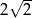 B)
B) 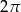 C)
C) 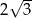 D) 2
D) 2
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 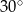 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 2 B) 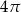 C)
C) 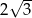 D)
D) 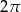
Dany jest stożek o objętości 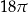 , którego przekrojem osiowym jest trójkąt
, którego przekrojem osiowym jest trójkąt 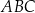 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 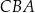 jest kątem nachylenia tworzącej
jest kątem nachylenia tworzącej 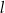 tego stożka do płaszczyzny jego podstawy. Tangens kąta
tego stożka do płaszczyzny jego podstawy. Tangens kąta 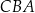 jest równy 2.
jest równy 2.
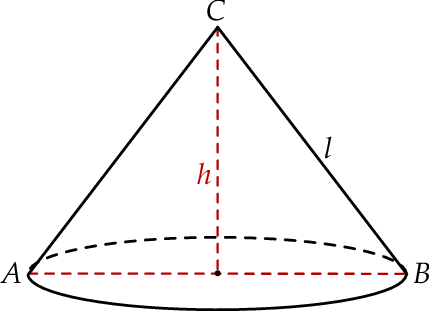
Wynika stąd, że wysokość 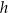 tego stożka jest równa
tego stożka jest równa
A) 12 B) 6 C) 4 D) 2
Przekrojem osiowym stożka o objętości 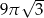 jest trójkąt równoboczny. Obwód tego trójkąta jest równy
jest trójkąt równoboczny. Obwód tego trójkąta jest równy
A) 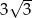 B)
B) 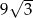 C) 18 D) 6
C) 18 D) 6
Przekrój osiowy stożka jest trójkątem równobocznym o boku  . Jeżeli
. Jeżeli  oznacza promień podstawy stożka,
oznacza promień podstawy stożka, 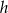 oznacza wysokość, to
oznacza wysokość, to
A) 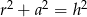 B)
B) 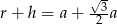 C)
C) 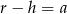 D)
D) 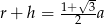
Przekrój osiowy stożka jest trójkątem równobocznym o wysokości 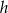 . Jeżeli
. Jeżeli  oznacza promień podstawy stożka,
oznacza promień podstawy stożka, 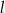 oznacza długość jego tworzącej, to
oznacza długość jego tworzącej, to
A) 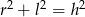 B)
B) 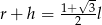 C)
C) 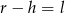 D)
D) 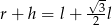
Tworząca stożka ma długość 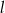 , a promień jego podstawy jest równy
, a promień jego podstawy jest równy  (zobacz rysunek).
(zobacz rysunek).
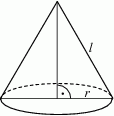
Powierzchnia boczna tego stożka jest 2 razy większa od pola jego podstawy. Wówczas
A) 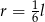 B)
B) 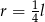 C)
C) 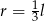 D)
D) 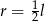
Tworząca stożka ma długość 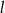 , a promień jego podstawy jest równy
, a promień jego podstawy jest równy  (zobacz rysunek).
(zobacz rysunek).
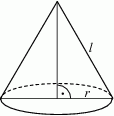
Powierzchnia boczna tego stożka jest 3 razy większa od pola jego podstawy. Wówczas
A) 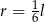 B)
B) 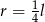 C)
C) 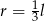 D)
D) 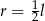
Półkole o promieniu 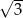 cm zwinięto w stożek.
cm zwinięto w stożek.
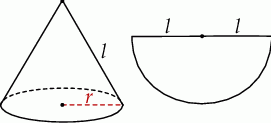
Wysokość tego stożka jest równa
A) 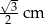 B)
B) 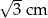 C) 3 cm D) 1,5 cm
C) 3 cm D) 1,5 cm
Pole powierzchni całkowitej pewnego stożka jest 3 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 2 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą
A) 12 B) 11 C) 24 D) 22
Pole powierzchni całkowitej pewnego stożka jest 4 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 3 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą
A) 42 B) 45 C) 48 D) 52
Trójkąt prostokątny 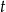 obrócono względem dłuższej przyprostokątnej i otrzymano stożek o polu powierzchni bocznej
obrócono względem dłuższej przyprostokątnej i otrzymano stożek o polu powierzchni bocznej 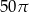 i kącie rozwarcia
i kącie rozwarcia 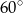 . Obwód trójkąta
. Obwód trójkąta 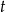 jest równy
jest równy
A) 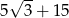 B)
B) 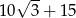 C)
C) 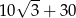 D)
D) 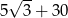
Pole powierzchni całkowitej pewnego stożka jest 5 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka jest nachylona do podstawy pod kątem  takim, że
takim, że
A) 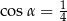 B)
B) 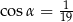 C)
C) 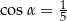 D)
D) 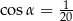
Kąt rozwarcia stożka ma miarę 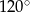 , a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 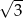 B)
B) 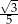 C) 5 D)
C) 5 D) 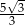
Kąt rozwarcia stożka ma miarę 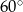 , a jego tworząca ma długość 8. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 8. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 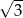 B)
B) 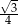 C)
C) 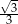 D)
D) 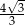
Kąt rozwarcia stożka ma miarę 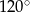 , a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
, a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
A) 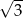 B)
B) 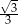 C)
C) 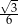 D)
D)