Do zbioru rozwiązań nierówności 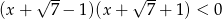 należy liczba
należy liczba
A) 0 B) -3 C) -1 D) 3
/Szkoła średnia/Zadania testowe/Nierówności/Kwadratowe/Pojedyncze rozwiązania
Do zbioru rozwiązań nierówności 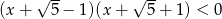 należy liczba
należy liczba
A) 0 B) 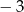 C)
C) 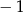 D) 3
D) 3
Do zbioru rozwiązań nierówności 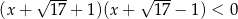 należy liczba
należy liczba
A) 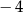 B)
B) 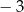 C)
C) 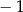 D) 3
D) 3
Do zbioru rozwiązań nierówności 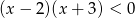 należy liczba
należy liczba
A) 9 B) 7 C) 4 D) 1
Do zbioru rozwiązań nierówności 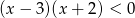 należy liczba
należy liczba
A) -3 B) 2 C) 3 D) -2
Do zbioru rozwiązań nierówności 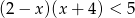 należy liczba
należy liczba
A) 1 B) -2 C) 3 D) -1
Do zbioru rozwiązań nierówności 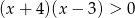 należy liczba
należy liczba
A) 7 B) 3 C) 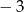 D) 1
D) 1
Przykładem liczby niewymiernej spełniającej nierówność 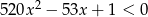 jest
jest
A) 0,04 B) 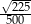 C)
C) 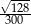 D)
D) 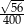
Najmniejszą liczbą naturalną, która nie spełnia nierówności 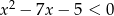 jest
jest
A) 0 B) 3 C) 7 D) 8
Największą liczbą naturalną, która nie spełnia nierówności 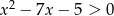 jest
jest
A) 0 B) 3 C) 7 D) 8
Największą liczbą całkowitą spełniającą nierówność 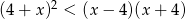 jest
jest
A) 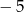 B)
B) 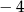 C)
C) 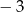 D)
D) 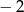
Liczb całkowitych spełniających nierówność 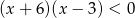 jest
jest
A) 8 B) 0 C) 7 D) nieskończenie wiele
Liczb całkowitych spełniających nierówność 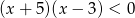 jest
jest
A) 8 B) 0 C) 7 D) 9
Liczb całkowitych spełniających nierówność 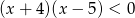 jest
jest
A) 0 B) 8 C) 7 D) 10
Liczb pierwszych należących do przedziału będącego rozwiązaniem nierówności 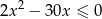 jest
jest
A) nieskończenie wiele B) 5 C) 6 D) 7
Liczb pierwszych należących do przedziału będącego rozwiązaniem nierówności 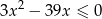 jest
jest
A) nieskończenie wiele B) 6 C) 7 D) 5
Liczb pierwszych należących do przedziału będącego rozwiązaniem nierówności 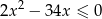 jest
jest
A) nieskończenie wiele B) 8 C) 6 D) 7
Do zbioru rozwiązań nierówności 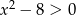 nie należy liczba:
nie należy liczba:
A) -3 B) 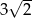 C) 5 D)
C) 5 D) 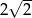
Do zbioru rozwiązań nierówności 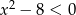 nie należy liczba:
nie należy liczba:
A) -2 B) 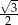 C) -3 D)
C) -3 D) 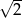
Do zbioru rozwiązań nierówności 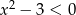 należy liczba:
należy liczba:
A) 2 B) 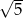 C) -3 D)
C) -3 D) 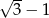
Do zbioru rozwiązań nierówności 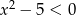 nie należy liczba:
nie należy liczba:
A) 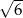 B)
B) 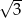 C) 2 D)
C) 2 D) 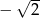
Do zbioru rozwiązań nierówności 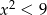 nie należy liczba
nie należy liczba
A) 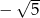 B)
B) 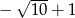 C)
C) 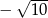 D)
D) 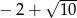
Do zbioru rozwiązań nierówności 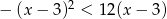 należy liczba
należy liczba
A) 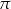 B)
B) 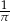 C)
C) 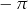 D)
D) 
Do zbioru rozwiązań nierówności 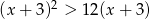 należy liczba
należy liczba
A)  B)
B)  C)
C) 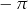 D)
D) 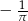
Do zbioru rozwiązań nierówności 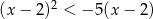 należy liczba
należy liczba
A) 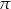 B)
B) 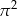 C)
C) 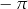 D)
D) 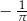
Do zbioru rozwiązań nierówności 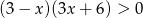 należy liczba
należy liczba
A) 3 B) 2 C) -2 D) -3
Do zbioru rozwiązań nierówności 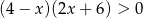 należy liczba
należy liczba
A) 3 B) 5 C) 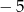 D)
D) 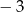
Największą liczbą naturalną, która spełnia nierówności 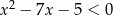 jest
jest
A) 0 B) 3 C) 7 D) 8
Największą liczbą naturalną, która spełnia nierówności 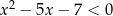 jest
jest
A) 0 B) 3 C) 7 D) 6

