W trapez prostokątny można wpisać okrąg. Jedna z jego podstaw ma długość  , druga jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu.
, druga jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Prostokątny opisany na okręgu
Środek okręgu wpisanego w trapez prostokątny, znajduje się w odległości 4 oraz 8 od końców dłuższego ramienia trapezu. Oblicz pole tego trapezu.
Środek okręgu wpisanego w trapez prostokątny znajduje się w odległości 2 cm i 4 cm od końców ramienia pochyłego danego trapezu. Znaleźć pole trapezu.
Promień koła wpisanego w trapez prostokątny jest równy  , kąt ostry trapezu równy jest
, kąt ostry trapezu równy jest  . Oblicz pole i obwód trapezu.
. Oblicz pole i obwód trapezu.
Trapez prostokątny 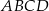 o podstawach
o podstawach 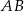 i
i 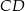 jest opisany na okręgu. Ramię
jest opisany na okręgu. Ramię 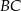 ma długość 10, a ramię
ma długość 10, a ramię 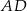 jest wysokością trapezu. Podstawa
jest wysokością trapezu. Podstawa 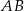 jest 2 razy dłuższa od podstawy
jest 2 razy dłuższa od podstawy 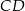 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Trapez prostokątny 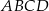 o podstawach
o podstawach 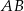 i
i 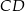 jest opisany na okręgu. Ramię
jest opisany na okręgu. Ramię 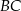 ma długość 15, a ramię
ma długość 15, a ramię 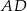 jest wysokością trapezu. Podstawa
jest wysokością trapezu. Podstawa 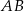 jest 3 razy dłuższa od podstawy
jest 3 razy dłuższa od podstawy 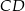 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Pole trapezu prostokątnego opisanego na okręgu jest równe 5, a obwód trapezu wynosi 10. Oblicz długość promienia okręgu.
Trapez prostokątny o podstawach  i
i 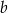 jest opisany na okręgu. Oblicz pole tego trapezu.
jest opisany na okręgu. Oblicz pole tego trapezu.
Na okręgu o średnicy 8 opisano trapez prostokątny, w którym jedna z podstaw ma długość 15. Oblicz pole tego trapezu.
Na okręgu o promieniu  opisano trapez prostokątny, którego najkrótszy bok ma długość
opisano trapez prostokątny, którego najkrótszy bok ma długość 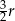 . Oblicz pole tego trapezu oraz stosunek długości jego przekątnych.
. Oblicz pole tego trapezu oraz stosunek długości jego przekątnych.
W trapez prostokątny wpisano okrąg o promieniu  . Najkrótszy bok tego trapezu ma długość
. Najkrótszy bok tego trapezu ma długość 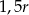 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
W trapez prostokątny 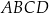 wpisano okrąg, przy czym punkt
wpisano okrąg, przy czym punkt 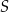 jest środkiem tego okręgu, a punkt
jest środkiem tego okręgu, a punkt 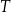 jest punktem styczności okręgu wpisanego z dłuższym ramieniem
jest punktem styczności okręgu wpisanego z dłuższym ramieniem 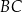 . Oblicz pole tego trapezu, jeśli
. Oblicz pole tego trapezu, jeśli 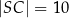 i
i 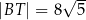 .
.

Trapez prostokątny 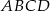 o podstawach
o podstawach 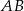 i
i 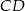 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  .
.
- Wykaż, że
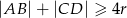 .
. - Wiedząc, że pole trapezu jest równe 4 wykaż, że
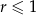 .
.
Dany jest trapez prostokątny 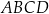 o kątach prostych przy wierzchołkach
o kątach prostych przy wierzchołkach 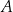 i
i 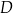 . Ramię
. Ramię 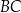 trapezu ma długość 5. W ten trapez wpisano okrąg o środku w punkcie
trapezu ma długość 5. W ten trapez wpisano okrąg o środku w punkcie 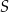 i promieniu 2. Punkt
i promieniu 2. Punkt 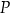 jest punktem styczności tego okręgu i dłuższej podstawy
jest punktem styczności tego okręgu i dłuższej podstawy 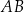 tego trapezu (zobacz rysunek).
tego trapezu (zobacz rysunek).
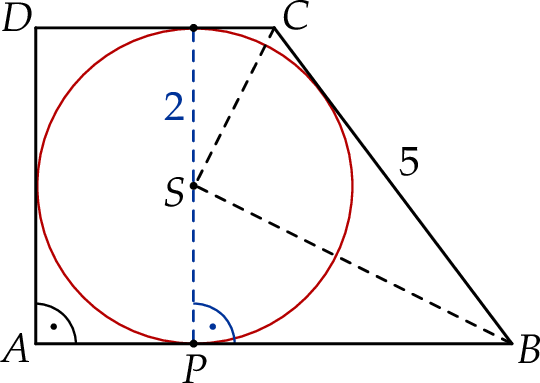
Wykaż, że trójkąty 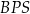 i
i 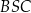 są trójkątami podobnymi, oraz oblicz skalę tego podobieństwa.
są trójkątami podobnymi, oraz oblicz skalę tego podobieństwa.

