W trójkącie 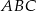 dane są
dane są 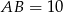 ,
, 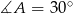 i
i 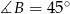 . Oblicz długości pozostałych boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
. Oblicz długości pozostałych boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Promienie okręgów
Jeden z boków trójkąta ma długość  , zaś kąty trójkąta przyległe do tego boku mają miary
, zaś kąty trójkąta przyległe do tego boku mają miary  i
i 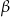 . Znajdź promień okręgu wpisanego w ten trójkąt.
. Znajdź promień okręgu wpisanego w ten trójkąt.
Dany jest trójkąt 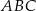 , w którym
, w którym 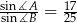 . Na boku
. Na boku 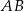 leży punkt
leży punkt 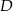 taki, że
taki, że 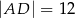 ,
, 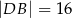 oraz
oraz 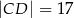 . Oblicz długość promienia okręgu opisanego na trójkącie
. Oblicz długość promienia okręgu opisanego na trójkącie 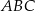 .
.
Trójkąt ostrokątny, którego boki mają długości 17 i 16 ma pole równe 64. Oblicz promień okręgu opisanego na tym trójkącie.
Punkt 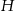 jest punktem wspólnym wysokości trójkąta ostrokątnego
jest punktem wspólnym wysokości trójkąta ostrokątnego 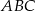 wpisanego w okrąg o promieniu 12. Oblicz promień okręgu opisanego na trójkącie
wpisanego w okrąg o promieniu 12. Oblicz promień okręgu opisanego na trójkącie 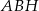 .
.
W trójkącie 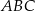 dane są kąt
dane są kąt 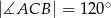 ,
, 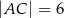 i
i 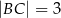 . Dwusieczna kąta
. Dwusieczna kąta 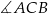 przecina bok
przecina bok 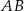 w punkcie
w punkcie 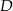 .
.
- Oblicz długość odcinka
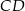 .
. - Jaki jest związek miedzy długościami promieni: okręgu opisanego na trójkącie
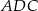 i okręgu opisanego na trójkącie
i okręgu opisanego na trójkącie 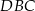 ? Odpowiedź uzasadnij.
? Odpowiedź uzasadnij.
Na trójkącie o bokach długości 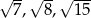 opisano okrąg. Oblicz promień tego okręgu.
opisano okrąg. Oblicz promień tego okręgu.
W okrąg o średnicy 16,25 wpisano trójkąt ostrokątny 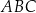 , w którym
, w którym 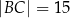 . Miary kątów
. Miary kątów 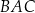 i
i 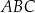 tego trójkąta spełniają warunek
tego trójkąta spełniają warunek
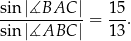
Oblicz promień okręgu wpisanego w trójkąt 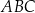 .
.
W trójkącie 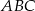 dane są długości boków:
dane są długości boków: 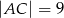 ,
, 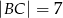 . Wiadomo też, że miara kąta
. Wiadomo też, że miara kąta 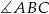 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 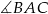 . Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.
. Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.
Dany jest trójkąt o bokach długości 7,8,9.
- Oblicz promień okręgu wpisanego w ten trójkąt.
- Oblicz sumę sinusów kątów tego trójkąta.
Pole trójkąta ostrokątnego o bokach 40 i 29 jest równe 420. Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Długości dwóch boków trójkąta są równe 1 i 4, a miara kąta zawartego między nimi wynosi 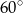 .
.
- Oblicz pole tego trójkąta.
- Oblicz promień okręgu opisanego na tym trójkącie.
- Oblicz promień okręgu wpisanego w ten trójkąt.

