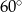Dany jest trapez 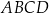 , w którym przekątna
, w którym przekątna 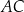 jest prostopadła do ramienia
jest prostopadła do ramienia 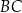 ,
, 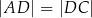 oraz
oraz 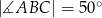 (zobacz rysunek).
(zobacz rysunek).
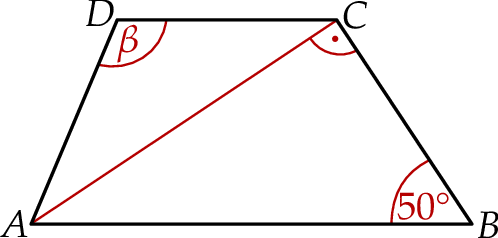
Stąd wynika, że
A) 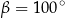 B)
B) 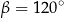 C)
C) 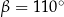 D)
D) 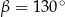
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trapez 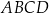 , w którym przekątna
, w którym przekątna 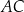 jest prostopadła do ramienia
jest prostopadła do ramienia 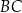 ,
, 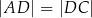 oraz
oraz 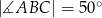 (zobacz rysunek).
(zobacz rysunek).
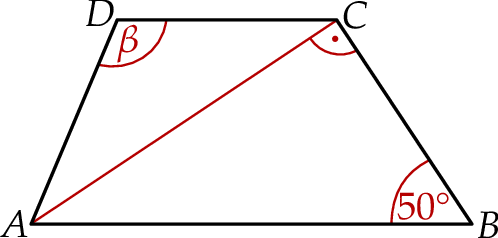
Stąd wynika, że
A) 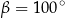 B)
B) 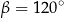 C)
C) 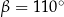 D)
D) 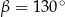
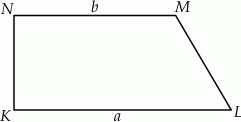
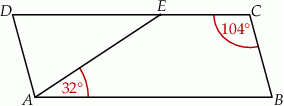
Dany jest trapez 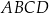 , w którym bok
, w którym bok 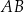 jest równoległy do boku
jest równoległy do boku 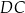 . W tym trapezie poprowadzono odcinek
. W tym trapezie poprowadzono odcinek 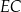 równoległy do boku
równoległy do boku 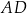 , podano miary dwóch kątów oraz oznaczono kąt
, podano miary dwóch kątów oraz oznaczono kąt  (zobacz rysunek).
(zobacz rysunek).

Kąt  ma miarę
ma miarę
A) 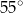 B)
B) 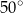 C)
C) 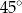 D)
D) 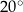
Dany jest trapez 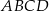 , w którym przekątna
, w którym przekątna 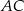 jest prostopadła do ramienia
jest prostopadła do ramienia 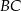 ,
, 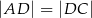 oraz
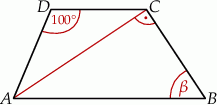
oraz 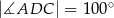 (zobacz rysunek).
(zobacz rysunek).
Stąd wynika, że
A) 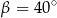 B)
B) 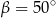 C)
C) 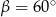 D)
D) 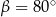
Dany jest trapez prostokątny 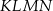 , którego podstawy mają długości
, którego podstawy mają długości 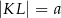 ,
, 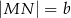 ,
, 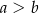 . Kąt
. Kąt 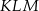 ma miarę
ma miarę 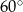 . Długość ramienia
. Długość ramienia 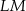 tego trapezu jest równa
tego trapezu jest równa
A) 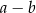 B)
B) 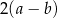 C)
C) 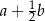 D)
D) 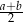
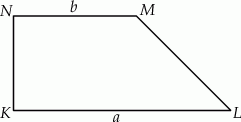
Dany jest trapez prostokątny 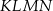 , którego podstawy mają długości
, którego podstawy mają długości 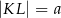 ,
, 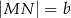 ,
, 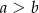 . Kąt
. Kąt 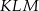 ma miarę
ma miarę 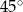 . Długość ramienia
. Długość ramienia 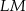 tego trapezu jest równa
tego trapezu jest równa
A) 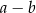 B)
B) 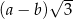 C)
C) 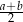 D)
D) 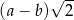
Przekątne trapezu równoramiennego przecinają się pod kątem 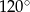 i dzielą się w stosunku 2:1. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
i dzielą się w stosunku 2:1. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeden z kątów trapezu ma miarę 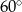 . . | P | F |
| Przekątna dzieli jeden z kątów trapezu w stosunku 3:1. | P | F |
W trapezie  przekątne przecinają się w punkcie
przekątne przecinają się w punkcie  . Pole trójkąta
. Pole trójkąta 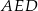 jest równe
jest równe 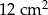 , a pole trójkąta
, a pole trójkąta 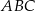 jest równe
jest równe 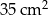 .
.
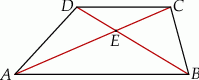
Pole trójkąta  jest równe
jest równe
A) 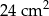 B)
B) 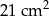 C)
C) 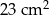 D)
D) 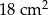
W trapezie 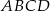 podstawa
podstawa 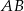 jest dłuższa od podstawy
jest dłuższa od podstawy 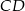 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta  jest równe połowie pola trapezu jest równe połowie pola trapezu  . . | P | F |
Suma pól trójkątów 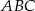 i i 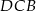 jest równa polu trapezu. jest równa polu trapezu. | P | F |
Wykonano następującą konstrukcję.
1. Narysowano trapez równoramienny 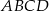 , w którym
, w którym 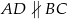 .
.
2. Wykreślono symetralne odcinków 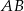 i
i 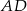 i ich punkt przecięcia oznaczono literą
i ich punkt przecięcia oznaczono literą  .
.
3. Narysowano okrąg o środku w punkcie 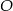 i promieniu
i promieniu  .
.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego trapezu.
B) jest styczny do wszystkich boków tego trapezu.
C) jest styczny do podstaw tego trapezu.
D) przechodzi przez środki ramion trapezu.
Na rysunku przedstawiono trapez 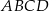 zbudowany z dwóch równoramiennych trójkątów prostokątnych. Krótsza przekątna tego trapezu ma długość 10 cm.
zbudowany z dwóch równoramiennych trójkątów prostokątnych. Krótsza przekątna tego trapezu ma długość 10 cm.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trapezu  jest równy jest równy 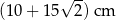 . . | P | F |
Pole trapezu 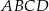 jest równe jest równe 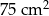 . . | P | F |
Na rysunku przedstawiono czworokąt 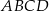 , w którym
, w którym 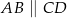 i trójkąt równoramienny
i trójkąt równoramienny 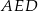 , w którym
, w którym 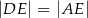 . Miara kąta
. Miara kąta 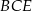 jest równa
jest równa 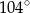 , a miara kąta
, a miara kąta 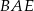 jest równa
jest równa 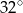 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 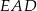 ma miarę ma miarę 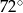 . . | P | F |
Czworokąt 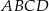 jest równoległobokiem. jest równoległobokiem. | P | F |
W trapezie 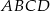 punkt
punkt 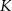 jest środkiem ramienia
jest środkiem ramienia 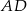 , a punkt
, a punkt 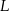 jest środkiem podstawy
jest środkiem podstawy 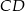 .
.
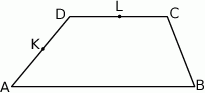
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 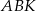 ma takie samo pole, jak trójkąt ma takie samo pole, jak trójkąt 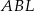 . . | P | F |
Pole trójkąta 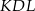 jest dwa razy mniejsze od pola trójkąta jest dwa razy mniejsze od pola trójkąta 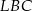 . . | P | F |
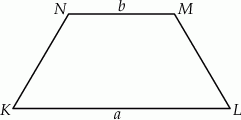
Dany jest trapez równoramienny 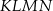 , którego podstawy mają długości
, którego podstawy mają długości 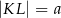 ,
, 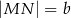 ,
, 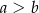 . Kąt
. Kąt 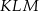 ma miarę
ma miarę 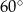 . Długość ramienia
. Długość ramienia 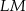 tego trapezu jest równa
tego trapezu jest równa
A) 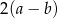 B)
B) 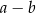 C)
C) 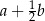 D)
D) 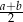
W trapezie równoramiennym 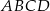 podstawy
podstawy 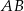 i
i 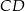 mają długości równe odpowiednio
mają długości równe odpowiednio  i
i 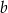 (przy czym
(przy czym 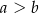 ). Miara kąta ostrego trapezu jest równa
). Miara kąta ostrego trapezu jest równa 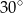 . Wtedy wysokość tego trapezu jest równa
. Wtedy wysokość tego trapezu jest równa
A) 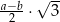 B)
B) 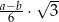 C)
C) 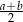 D)
D) 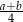
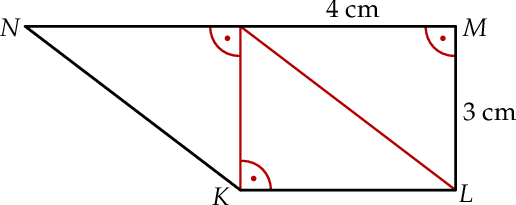
Na rysunku przedstawiono trapez 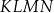 zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości 3 cm i 4 cm.
zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości 3 cm i 4 cm.
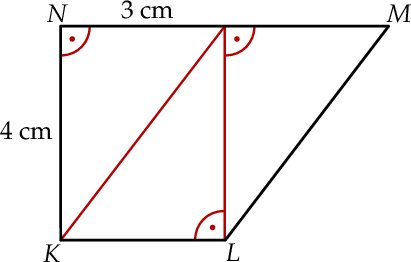
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trapezu  jest równe jest równe  . . | P | F |
Obwód trapezu  jest równy 18 cm. jest równy 18 cm. | P | F |
Na rysunku przedstawiono trapez  zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości 3 cm i 4 cm.
zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości 3 cm i 4 cm.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trapezu  jest równe jest równe 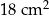 . . | P | F |
Obwód trapezu 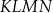 jest równy 18 cm. jest równy 18 cm. | P | F |
Prosta 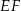 dzieli trapez równoramienny
dzieli trapez równoramienny 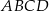 na romb
na romb 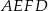 o obwodzie 52 cm i trapez
o obwodzie 52 cm i trapez  o obwodzie o 13 cm mniejszym od obwodu rombu
o obwodzie o 13 cm mniejszym od obwodu rombu  .
.
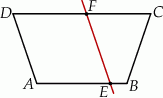
Suma długości odcinków  i
i 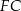 jest równa
jest równa
A) 14 cm B) 13 cm C) 15 cm D) 18 cm
Podstawy trapezu mają długości 9 cm i 12 cm, a jedno z jego ramion ma długość 7 cm.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód tego trapezu może być równy 56 cm. | P | F |
Pole tego trapezu może być równe 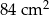 . . | P | F |
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 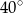 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 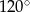 B)
B) 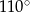 C)
C) 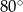 D)
D) 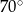
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 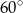 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 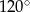 B)
B) 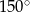 C)
C) 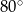 D)
D) 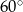
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 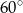 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 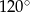 B)
B) 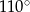 C)
C) 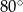 D)
D) 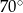
Różnica miar dwóch kątów rozwartych trapezu jest równa 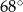 . Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
. Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
A) 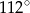 B)
B) 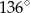 C)
C) 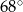 D)
D) 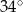
Dany jest trapez prostokątny 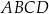 , w którym
, w którym 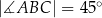 . Punkty
. Punkty 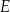 i
i 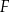 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 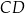 i
i 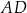 .
.

Długość odcinka 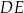 jest równa 6, a długość odcinka
jest równa 6, a długość odcinka 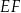 jest równa 10. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest równa 10. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trapezu 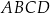 jest liczbą całkowitą. jest liczbą całkowitą. | P | F |
Pole trapezu 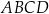 jest równe 320. jest równe 320. | P | F |
Przekątne trapezu  przedstawionego na rysunku przecinają się w punkcie
przedstawionego na rysunku przecinają się w punkcie  .
.
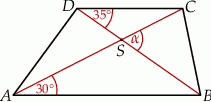
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt  ma miarę ma miarę 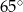 . . | P | F |
Trójkąty 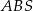 i i 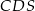 mają równe kąty. mają równe kąty. | P | F |
Krótsze ramię trapezu prostokątnego ma długość 4 cm, a jego krótsza podstawa ma długość 3 cm. Kąt ostry tego trapezu ma miarę 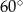 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wysokość tego trapezu ma długość 4 cm. | P | F |
Pole tego trapezu jest równe 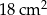 . . | P | F |
Dany jest trapez prostokątny 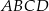 , w którym
, w którym 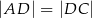 oraz
oraz 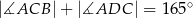 (zobacz rysunek).
(zobacz rysunek).
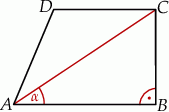
Stąd wynika, że
A) 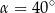 B)
B) 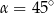 C)
C) 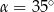 D)
D) 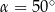
Kąty wewnętrzne przy wierzchołkach  i
i  trapezu
trapezu  są równe odpowiednio
są równe odpowiednio 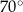 i
i 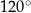 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 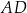 i
i 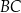 przecinają się pod kątem
przecinają się pod kątem
A) 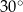 B)
B) 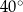 C)
C) 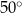 D)
D) 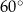
Kąty wewnętrzne przy wierzchołkach 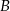 i
i 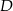 trapezu
trapezu 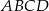 są równe odpowiednio
są równe odpowiednio 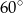 i
i 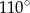 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 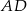 i
i 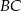 przecinają się pod kątem
przecinają się pod kątem
A) 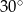 B)
B) 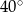 C)
C) 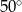 D)
D)