Dany jest czworokąt 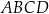 . Niech
. Niech 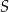 będzie punktem przecięcia jego przekątnych. Udowodnij, że czworokąt
będzie punktem przecięcia jego przekątnych. Udowodnij, że czworokąt 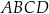 można wpisać w okrąg wtedy i tylko wtedy, gdy
można wpisać w okrąg wtedy i tylko wtedy, gdy 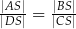 .
.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Oblicz promień okręgu opisanego na trapezie równoramiennym, w którym sinus kąta ostrego jest równy  , a przekątna ma długość 12.
, a przekątna ma długość 12.
Jedna z przekątnych rombu jest dwa razy dłuższa od drugiej. Wyznacz stosunek obwodu rombu do sumy jego przekątnych.
Trapez równoramienny o przekątnej długości 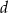 i ramieniu długości
i ramieniu długości  jest opisany na okręgu. Wykaż, że odległość środka okręgu wpisanego w ten trapez od końca krótszej podstawy jest równa
jest opisany na okręgu. Wykaż, że odległość środka okręgu wpisanego w ten trapez od końca krótszej podstawy jest równa 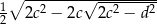 .
.
Podstawy trapezu równoramiennego mają długości 3 i 5, a jego ramię ma długość 2. Oblicz promień okręgu opisanego na tym trapezie.
Trapez równoramienny jest opisany na okręgu. Suma długości krótszej podstawy i ramienia trapezu jest równa 30. Wyraź pole tego trapezu jako funkcję długości jego ramienia. Wyznacz dziedzinę tej funkcji.
W prostokącie 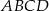 połączono wierzchołki
połączono wierzchołki 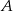 i
i 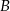 ze środkiem boku
ze środkiem boku 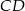 i otrzymano trójkąt, którego jeden z kątów ma miarę
i otrzymano trójkąt, którego jeden z kątów ma miarę 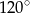 . Wiedząc, że
. Wiedząc, że 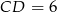 oblicz obwód prostokąta
oblicz obwód prostokąta 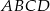 .
.
W równoległoboku, w którym boki mają długości 1 i 3, symetralna krótszego boku przechodzi przez wierzchołek równoległoboku. Znajdź długości przekątnych tego równoległoboku.
Przekątna 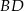 rombu
rombu 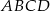 przecina jego wysokość
przecina jego wysokość 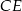 , poprowadzoną na bok
, poprowadzoną na bok 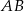 , w punkcie
, w punkcie 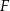 . Oblicz pole rombu
. Oblicz pole rombu 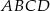 , jeśli wiadomo, że
, jeśli wiadomo, że 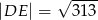 oraz
oraz 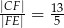 .
.
W trapezie 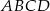 boki nierównoległe
boki nierównoległe 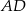 i
i 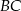 zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane
zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane 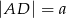 oraz
oraz 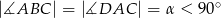 .
.
Dany jest prostokąt 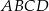 , w którym
, w którym 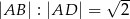 . Punkt
. Punkt 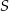 jest środkiem boku
jest środkiem boku 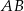 . Oblicz miarę kąta między prostymi
. Oblicz miarę kąta między prostymi 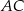 i
i 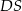 .
.
Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.
Trapez równoramienny 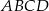 o podstawach
o podstawach 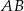 i
i 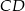 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Wykaż, że
. Wykaż, że 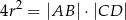 .
.
Połączono ramiona trapezu odcinkiem równoległym do podstaw i dzielącym te ramiona w stosunku 2:3 licząc od krótszej podstawy. Oblicz długość tego odcinka, jeśli wiesz, że podstawy trapezu mają długości  i
i 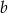 , gdzie
, gdzie 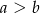 .
.
Na okręgu o promieniu  opisano trapez równoramienny, którego długość jednej z podstaw wynosi
opisano trapez równoramienny, którego długość jednej z podstaw wynosi 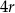 . Oblicz odległość środka okręgu od wierzchołków trapezu.
. Oblicz odległość środka okręgu od wierzchołków trapezu.
Prostokąt jest wpisany w okrąg o promieniu 10, a jego dłuższe boki są styczne do okręgu o promieniu 3.
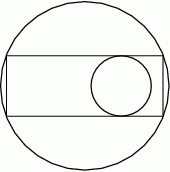
Oblicz pole tego prostokąta.
W trapez równoramienny, który nie jest równoległobokiem, wpisano okrąg promieniu 4 cm. Ramię trapezu ma długość 10 cm. Punkty styczności okręgu z ramionami trapezu dzielą obwód trapezu na dwie częsci. Oblicz stosunek długości tych części.
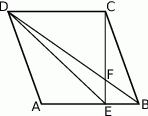
Na bokach 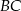 i
i 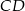 równoległoboku
równoległoboku 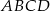 zbudowano kwadraty
zbudowano kwadraty 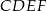 i
i 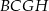 (zobacz rysunek).
(zobacz rysunek).
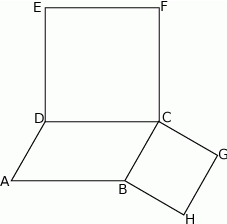
Udowodnij, że 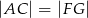 .
.
W trapezie równoramiennym przekątna ma długość 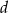 i tworzy z dłuższą podstawą kąt o mierze
i tworzy z dłuższą podstawą kąt o mierze  . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Obwód czworokąta wypukłego 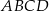 jest równy 50 cm. Obwód trójkąta
jest równy 50 cm. Obwód trójkąta 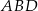 jest równy 46 cm, a obwód trójkąta
jest równy 46 cm, a obwód trójkąta 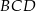 jest równy 36 cm. Oblicz długość przekątnej
jest równy 36 cm. Oblicz długość przekątnej 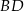 .
.
Pole trapezu równoramiennego opisanego na okręgu jest równe 80, a cosinus kąta rozwartego tego trapezu jest równy 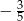 . Oblicz długość ramienia tego trapezu.
. Oblicz długość ramienia tego trapezu.

