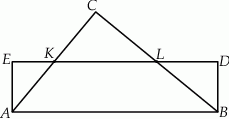
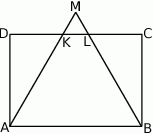
Na rysunku przedstawiono prostokąt 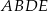 i trójkąt
i trójkąt 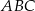 . Punkty
. Punkty 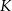 i
i 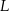 dzielą odcinki
dzielą odcinki 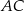 i
i 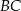 na połowy. Uzasadnij, że pole prostokąta
na połowy. Uzasadnij, że pole prostokąta 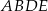 jest równe polu trójkąta
jest równe polu trójkąta 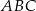 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono prostokąt 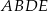 i trójkąt
i trójkąt 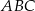 . Punkty
. Punkty 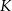 i
i 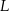 dzielą odcinki
dzielą odcinki 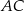 i
i 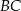 na połowy. Uzasadnij, że pole prostokąta
na połowy. Uzasadnij, że pole prostokąta 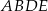 jest równe polu trójkąta
jest równe polu trójkąta 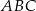 .
.

Dany jest trapez równoramienny 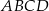 o obwodzie
o obwodzie 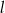 i podstawach
i podstawach 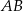 oraz
oraz 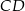 takich, że
takich, że 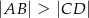 . Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna
. Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna 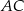 trapezu ma długość
trapezu ma długość 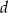 (zobacz rysunek).
(zobacz rysunek).
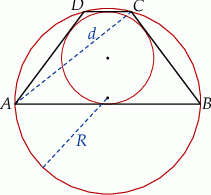
Wykaż, że promień 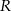 okręgu opisanego na trapezie
okręgu opisanego na trapezie 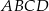 jest równy
jest równy 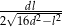 .
.
Kąt ostry rombu 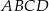 ma miarę
ma miarę 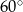 . Na bokach
. Na bokach 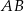 i
i 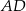 tego rombu wybrano punkty – odpowiednio –
tego rombu wybrano punkty – odpowiednio – 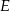 i
i 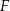 takie, że
takie, że 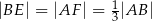 . Odcinki
. Odcinki 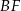 i
i 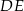 przecinają się w punkcie
przecinają się w punkcie 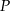 (zobacz rysunek).
(zobacz rysunek).
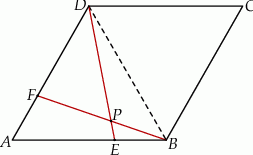
Wykaż, że punkt 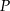 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 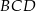 .
.
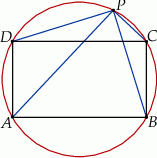
Punkt 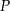 należy do okręgu opisanego na prostokącie
należy do okręgu opisanego na prostokącie 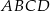 . Wykaż, że
. Wykaż, że 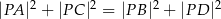 .
.
Ramiona trapezu prostokątnego mają długości 6 i 10. Odcinek łączący środki ramion ma długość 10. Oblicz długości podstaw trapezu.
Punkt 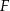 jest środkiem boku
jest środkiem boku 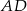 prostokąta
prostokąta 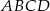 , w którym
, w którym 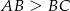 . Punkt
. Punkt 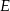 jest takim punktem boku
jest takim punktem boku 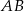 tego prostokąta, że prosta
tego prostokąta, że prosta 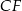 jest dwusieczną kąta
jest dwusieczną kąta 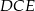 . Wykaż, że trójkąt
. Wykaż, że trójkąt 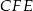 jest prostokątny.
jest prostokątny.
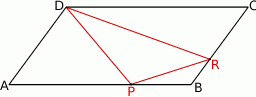
Dany jest równoległobok 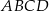 , w którym kąt rozwarty
, w którym kąt rozwarty 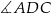 ma miarę
ma miarę 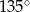 . Ponadto wiadomo, że
. Ponadto wiadomo, że 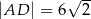 i
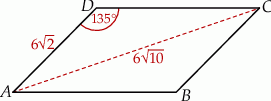
i 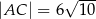 (zobacz rysunek). Oblicz obwód tego równoległoboku.
(zobacz rysunek). Oblicz obwód tego równoległoboku.
Krótsza przekątna trapezu prostokątnego dzieli trapez na dwa trójkąty, z których jeden jest równoboczny. Znajdź pole tego trapezu wiedząc, że ramię prostopadłe do podstaw ma długość 2.
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa 6. Oblicz pole tego trapezu.
Dany jest trapez prostokątny 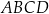 o kątach prostych przy wierzchołkach
o kątach prostych przy wierzchołkach 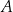 i
i 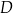 . Ramię
. Ramię 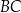 trapezu ma długość 5. W ten trapez wpisano okrąg o środku w punkcie
trapezu ma długość 5. W ten trapez wpisano okrąg o środku w punkcie 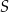 i promieniu 2. Punkt
i promieniu 2. Punkt 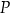 jest punktem styczności tego okręgu i dłuższej podstawy
jest punktem styczności tego okręgu i dłuższej podstawy 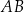 tego trapezu (zobacz rysunek).
tego trapezu (zobacz rysunek).
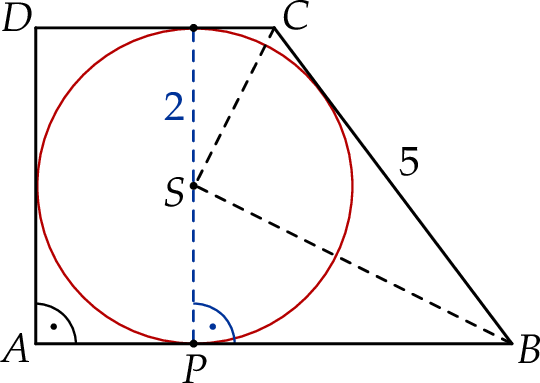
Wykaż, że trójkąty 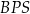 i
i 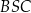 są trójkątami podobnymi, oraz oblicz skalę tego podobieństwa.
są trójkątami podobnymi, oraz oblicz skalę tego podobieństwa.
Suma miar dwóch sąsiednich kątów trapezu jest równa 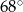 , a różnica miar dwóch pozostałych kątów jest równa
, a różnica miar dwóch pozostałych kątów jest równa 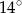 . Oblicz miary kątów tego trapezu.
. Oblicz miary kątów tego trapezu.
Dwa prostokąty podobne mają obwody równe odpowiednio 21 cm i 7 cm, a pole większego wynosi 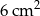 . Oblicz pole mniejszego prostokąta.
. Oblicz pole mniejszego prostokąta.
Czworokąt 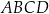 , w którym
, w którym 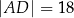 i
i 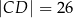 , jest opisany na okręgu. Kąt
, jest opisany na okręgu. Kąt 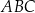 tego czworokąta jest rozwarty, a promień okręgu opisanego na trójkącie
tego czworokąta jest rozwarty, a promień okręgu opisanego na trójkącie 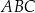 jest równy 12,5. Obwód czworokąta
jest równy 12,5. Obwód czworokąta 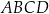 jest równy 66. Oblicz długość przekątnej
jest równy 66. Oblicz długość przekątnej 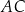 tego czworokąta.
tego czworokąta.
Podstawy trapezu prostokątnego mają długości 70 i 30, kąt ostry trapezu ma miarę 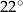 . Oblicz pole trapezu, przyjmując, że
. Oblicz pole trapezu, przyjmując, że 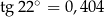 .
.
Podstawy trapezu prostokątnego mają długości 6 i 10 oraz tangens kąta ostrego jest równy 3. Oblicz pole tego trapezu.
Stosunek pola rombu do pola koła wpisanego w ten romb wynosi 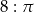 . Oblicz miarę kąta ostrego rombu.
. Oblicz miarę kąta ostrego rombu.
Punkty 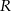 i
i 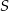 są środkami boków odpowiednio
są środkami boków odpowiednio 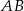 i
i 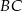 równoległoboku
równoległoboku 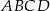 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 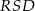 jest równe
jest równe pola tego równoległoboku.
pola tego równoległoboku.
Dany jest czworokąt 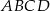 , którego kolejne boki mają długości 4,5,7,8. Kat między najkrótszymi bokami ma miarę
, którego kolejne boki mają długości 4,5,7,8. Kat między najkrótszymi bokami ma miarę  , taką że
, taką że 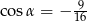 . Sprawdź czy na tym czworokącie można opisać okrąg.
. Sprawdź czy na tym czworokącie można opisać okrąg.
W równoległoboku 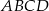 punkt
punkt 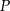 jest takim punktem boku
jest takim punktem boku 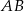 , że
, że 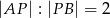 . Punkt
. Punkt 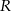 jest takim punktem boku
jest takim punktem boku 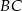 , że
, że 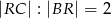 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 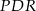 jest 5 razy większe od pola trójkąta
jest 5 razy większe od pola trójkąta 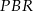 .
.
W prostokącie  punkt
punkt 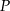 jest środkiem boku
jest środkiem boku 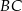 , a punkt
, a punkt 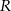 jest środkiem boku
jest środkiem boku 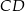 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 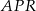 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 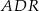 oraz
oraz 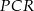 .
.
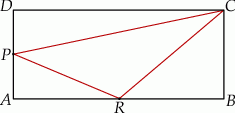
W prostokącie 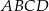 punkt
punkt 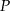 jest środkiem boku
jest środkiem boku 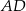 , a punkt
, a punkt 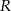 jest środkiem boku
jest środkiem boku 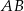 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 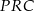 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 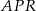 oraz
oraz 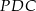 .
.
Dany jest prostokąt 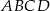 , w którym
, w którym 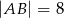 i
i 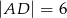 . Na boku
. Na boku 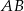 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 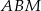 (patrz rysunek). Oblicz obwód trójkąta
(patrz rysunek). Oblicz obwód trójkąta  .
.
W równoległoboku boki mają długości 3 i 7, a jedna z przekątnych ma długość 6. Oblicz cosinus kąta ostrego pod jakim przecinają się przekątne tego równoległoboku.
