Punkt  leży na boku
leży na boku  kwadratu
kwadratu  oraz
oraz 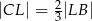 . Punkt
. Punkt 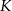 leży na przekątnej
leży na przekątnej 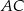 i odcinek
i odcinek 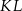 jest prostopadły do
jest prostopadły do 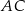 (zobacz rysunek).
(zobacz rysunek).
Wykaż, że 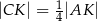 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkt  leży na boku
leży na boku  kwadratu
kwadratu  oraz
oraz 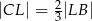 . Punkt
. Punkt  leży na przekątnej
leży na przekątnej 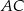 i odcinek
i odcinek 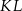 jest prostopadły do
jest prostopadły do 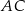 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że 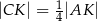 .
.
W trapezie prostokątnym 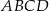 (rysunek) punkt
(rysunek) punkt 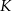 jest punktem przecięcia wysokości
jest punktem przecięcia wysokości 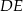 i przekątnej
i przekątnej 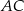 tego trapezu. Wiedząc, że
tego trapezu. Wiedząc, że 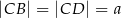 i
i 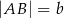 wykaż, że pole
wykaż, że pole  czworokąta
czworokąta 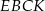 jest równe
jest równe 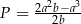 .
.
W równoległoboku  przekątna
przekątna 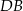 ma długość 7. Wiedząc, że obwód równoległoboku wynosi 26,
ma długość 7. Wiedząc, że obwód równoległoboku wynosi 26, 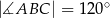 , oblicz długości boków równoległoboku.
, oblicz długości boków równoległoboku.
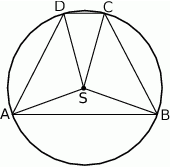
Przekątne czworokąta wypukłego 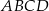 dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt
dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt 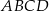 można wpisać okrąg.
można wpisać okrąg.
Dany jest kwadrat 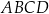 o boku długości
o boku długości  . Punkt
. Punkt 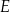 jest środkiem boku
jest środkiem boku 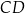 . Przekątna
. Przekątna 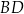 dzieli trójkąt
dzieli trójkąt 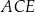 na dwie figury:
na dwie figury: 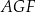 oraz
oraz 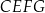 (zobacz rysunek).
(zobacz rysunek).
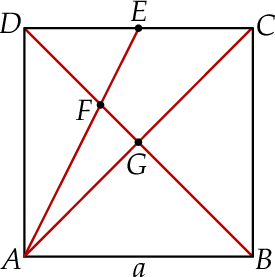
Oblicz pola figur 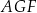 oraz
oraz 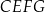 .
.
W trapezie opisanym na okręgu kąty przy dłuższej podstawie mają miary 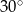 i
i 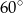 , a długość wysokości tego trapezu jest równa 6. Sporządź odpowiedni rysunek i oznacz jego elementy. Oblicz pole trapezu oraz długości jego podstaw.
, a długość wysokości tego trapezu jest równa 6. Sporządź odpowiedni rysunek i oznacz jego elementy. Oblicz pole trapezu oraz długości jego podstaw.
Podstawy trapezu równoramiennego mają długości  i
i 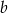 , gdzie
, gdzie 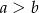 . Z wierzchołka kąta rozwartego trapezu poprowadzono wysokość. Uzasadnij, że wysokość ta dzieli dłuższą podstawę na odcinki o długościach
. Z wierzchołka kąta rozwartego trapezu poprowadzono wysokość. Uzasadnij, że wysokość ta dzieli dłuższą podstawę na odcinki o długościach 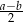 i
i 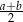 .
.
W trapez prostokątny 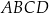 wpisano okrąg, przy czym punkt
wpisano okrąg, przy czym punkt 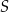 jest środkiem tego okręgu, a punkt
jest środkiem tego okręgu, a punkt 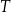 jest punktem styczności okręgu wpisanego z dłuższym ramieniem
jest punktem styczności okręgu wpisanego z dłuższym ramieniem 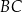 . Oblicz pole tego trapezu, jeśli
. Oblicz pole tego trapezu, jeśli 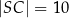 i
i 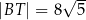 .
.

Bok rombu ma długość 13 cm, a jedna z jego przekątnych ma długość 24 cm. Oblicz długość drugiej przekątnej.
Punkt 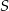 jest środkiem okręgu opisanego na trapezie równoramiennym
jest środkiem okręgu opisanego na trapezie równoramiennym 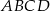 . Kąt
. Kąt 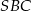 jest dwa razy większy od kąta
jest dwa razy większy od kąta 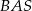 , a kąt
, a kąt 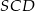 jest dwa razy większy od kąta
jest dwa razy większy od kąta 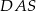 . Oblicz kąty trapezu
. Oblicz kąty trapezu 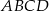 .
.
Oblicz pole prostokąta, którego przekątna ma długość 7 cm, a jeden z boków ma długość 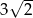 cm.
cm.
W czworokącie 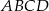 o obwodzie 24 dane są
o obwodzie 24 dane są 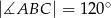 oraz
oraz 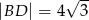 . Wiedząc, że środek przekątnej
. Wiedząc, że środek przekątnej 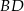 jest środkiem symetrii tego czworokąta oblicz jego pole.
jest środkiem symetrii tego czworokąta oblicz jego pole.
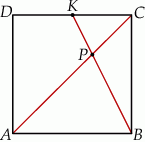
Na boku 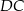 kwadratu
kwadratu 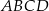 obrano punkt
obrano punkt 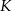 tak, że
tak, że 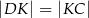 . Przekątna
. Przekątna 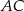 kwadratu przecina odcinek
kwadratu przecina odcinek 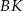 w punkcie
w punkcie 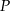 . Uzasadnij, że pole trójkąta
. Uzasadnij, że pole trójkąta 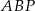 jest czterokrotnie większe niż pole trójkąta
jest czterokrotnie większe niż pole trójkąta 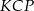 .
.
Trapez równoramienny 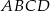 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Przekątna trapezu tworzy z dłuższą podstawą kąt
. Przekątna trapezu tworzy z dłuższą podstawą kąt  . Wyznacz obwód tego trapezu.
. Wyznacz obwód tego trapezu.
Na bokach 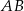 i
i 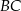 prostokąta
prostokąta 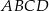 wybrano punkty
wybrano punkty 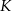 i
i 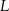 w ten sposób, że trójkąt
w ten sposób, że trójkąt 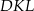 jest ostrokątny oraz
jest ostrokątny oraz 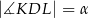 . Odcinek
. Odcinek 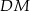 jest wysokością trójkąta
jest wysokością trójkąta 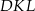 .
.
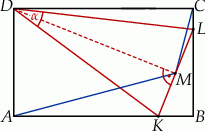
Wykaż, że 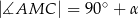 .
.
Podstawy trapezu mają długości 9 i 12. Oblicz długość odcinka łączącego środki przekątnych tego trapezu.
Na okręgu o danym promieniu  opisano trapez równoramienny
opisano trapez równoramienny 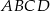 o dłuższej podstawie
o dłuższej podstawie 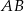 i krótszej
i krótszej 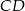 . Punkt styczności
. Punkt styczności 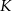 dzieli ramię
dzieli ramię 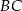 tak, że
tak, że 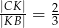 .
.
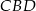 .
.Przez każde dwa sąsiednie wierzchołki czworokąta 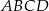 wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
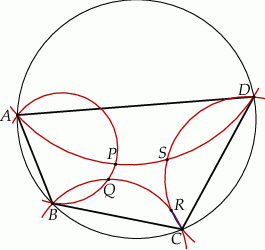
Wykaż, że punkty  , w których przecinają się te okręgi, leżą na jednym okręgu.
, w których przecinają się te okręgi, leżą na jednym okręgu.
Trapez prostokątny  o podstawach
o podstawach  i
i 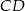 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  .
.
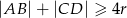 .
. 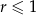 .
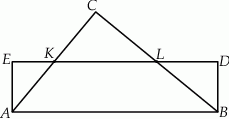
.Na rysunku przedstawiono prostokąt  i trójkąt
i trójkąt 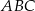 . Punkty
. Punkty 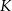 i
i 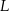 dzielą odcinki
dzielą odcinki 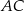 i
i 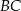 na połowy. Uzasadnij, że pole prostokąta
na połowy. Uzasadnij, że pole prostokąta 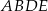 jest równe polu trójkąta
jest równe polu trójkąta 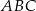 .
.