Przekątna trapezu równoramiennego tworzy z dłuższą podstawą kąt 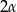 , a z ramieniem kąt
, a z ramieniem kąt  . Wykaż, że stosunek pól trójkątów, na które został podzielony trapez tą przekątną, jest równy
. Wykaż, że stosunek pól trójkątów, na które został podzielony trapez tą przekątną, jest równy 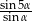 .
.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Dany jest prostokąt 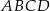 . Na boku
. Na boku 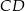 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 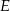 , że
, że 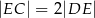 , a na boku
, a na boku 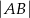 wybrano taki punkt
wybrano taki punkt 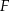 , że
, że 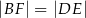 . Niech
. Niech 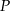 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 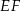 z prostą
z prostą 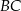 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 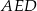 i
i  są przystające.
są przystające.
Dany jest prostokąt  . Na boku
. Na boku 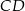 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 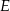 , że
, że 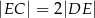 , a na przedłużeniu boku
, a na przedłużeniu boku 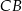 wybrano taki punkt
wybrano taki punkt 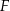 , że
, że 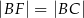 . Niech
. Niech 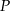 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 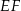 z prostą
z prostą 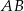 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 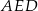 i
i 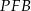 są przystające.
są przystające.
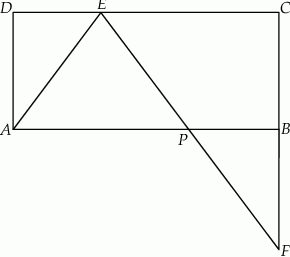
W prostokącie 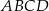 wierzchołek
wierzchołek 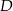 połączono odcinkami ze środkami
połączono odcinkami ze środkami 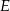 i
i 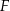 boków
boków 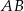 i
i 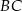 , zaś
, zaś 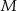 i
i 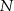 to punkty przecięcia tych odcinków z przekątną
to punkty przecięcia tych odcinków z przekątną 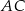 .
.
- Uzasadnij, że odcinki
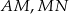 i
i 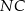 są jednakowej długości.
są jednakowej długości. - Uzasadnij, że trójkąty
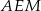 i
i  mają równe pola.
mają równe pola.
Prosta  przechodząca przez punkt przecięcia przekątnych trapezu
przechodząca przez punkt przecięcia przekątnych trapezu  przecina jego podstawy
przecina jego podstawy 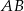 i
i 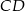 odpowiednio w punktach
odpowiednio w punktach 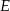 i
i 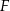 . Wykaż, że
. Wykaż, że 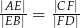 .
.
Na trapezie opisano okrąg o promieniu długości 25 cm. Dłuższa podstawa trapezu jest średnicą tego okręgu. Wiedząc że przekątna tego trapezu ma długość 40 cm, oblicz obwód tego trapezu.
Jeżeli skrócimy dłuższą przekątną rombu przy każdym wierzchołku o 4 cm, zaś przedłużymy krótszą przekątną o 1 cm, to otrzymamy kwadrat. Pole otrzymanego kwadratu jest o 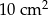 mniejsze od pola rombu. Oblicz pole rombu i pole kwadratu.
mniejsze od pola rombu. Oblicz pole rombu i pole kwadratu.
Dany jest czworokąt wypukły 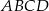 , w którym:
, w którym: 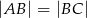 ,
, 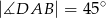 ,
, 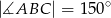 ,
, 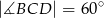 . Wykaż, że trójkąt
. Wykaż, że trójkąt 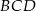 jest równoboczny.
jest równoboczny.
Ramię trapezu równoramiennego ma długość 12 cm. Kąt ostry tego trapezu ma miarę dwa razy mniejszą niż kąt rozwarty, a przekątna trapezu jest prostopadła do ramienia. Oblicz pole trapezu.
Ramię trapezu równoramiennego ma długość 18 cm. Kąt rozwarty tego trapezu ma miarę dwa razy większą niż kąt ostry, a przekątna trapezu jest prostopadła do ramienia. Oblicz pole trapezu.
Przekątna równoległoboku, poprowadzona z wierzchołka kąta rozwartego, ma długość 18 cm i dzieli ten kąta na kąty o miarach 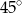 i
i 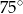 . Oblicz pole równoległoboku. Wynik przedstaw w postaci
. Oblicz pole równoległoboku. Wynik przedstaw w postaci 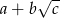 , gdzie
, gdzie 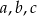 są liczbami naturalnymi.
są liczbami naturalnymi.
Na czworokącie 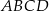 można opisać okrąg. Długości boków tego czworokąta są równe
można opisać okrąg. Długości boków tego czworokąta są równe 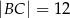 ,
, 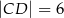 ,
, 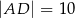 , a kąt
, a kąt 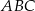 ma miarę
ma miarę 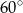 . Oblicz długość promienia okręgu opisanego na czworokącie
. Oblicz długość promienia okręgu opisanego na czworokącie 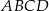 .
.
W trapezie równoramiennym 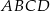 dłuższa podstawa
dłuższa podstawa 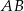 ma taką samą długość jak jego przekątna
ma taką samą długość jak jego przekątna 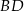 , a długość krótszej podstawy
, a długość krótszej podstawy 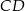 jest równa wysokości trapezu. Oblicz w jakim stosunku dzielą się przekątne tego trapezu.
jest równa wysokości trapezu. Oblicz w jakim stosunku dzielą się przekątne tego trapezu.
Długości boków prostokąta 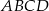 są równe:
są równe: 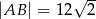 i
i 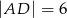 . Na odcinku
. Na odcinku 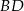 wybrano punkt
wybrano punkt 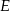 w ten sposób, że
w ten sposób, że 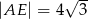 . Oblicz długość odcinka
. Oblicz długość odcinka 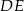 .
.
Trapez, w którym jedna z podstaw jest dwa razy dłuższa od drugiej, podzielono odcinkiem łączącym środki ramion trapezu na dwa czworokąty. Oblicz stosunek pól otrzymanych czworokątów.
Podstawy trapezu 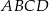 mają długości
mają długości 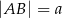 i
i 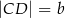 , przy czym
, przy czym 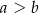 . Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość
. Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość 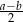 .
.
Przekątna trapezu równoramiennego dzieli jego kąt ostry na kąty o miarach  i
i 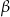 (
( – kąt między przekątną i podstawą). Wyznacz stosunek pól trójkątów, na jakie przekątna ta podzieliła trapez.
– kąt między przekątną i podstawą). Wyznacz stosunek pól trójkątów, na jakie przekątna ta podzieliła trapez.
W prostokącie 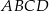 , w którym
, w którym 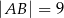 ,
, 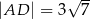 , na przekątnej
, na przekątnej 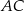 wybrano taki punkt
wybrano taki punkt 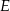 , że
, że 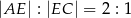 . Oblicz sinus kąta
. Oblicz sinus kąta 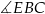 .
.
W prostokącie 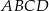 , w którym
, w którym 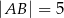 ,
, 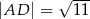 , na przekątnej
, na przekątnej 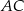 wybrano taki punkt
wybrano taki punkt 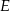 , że
, że 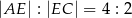 . Oblicz sinus kąta
. Oblicz sinus kąta 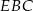 .
.
Przekątne prostokąta mają długość 20 cm i przecinają się pod kątem 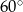 . Oblicz obwód tego prostokąta.
. Oblicz obwód tego prostokąta.
Oblicz pole czworokąta wypukłego 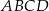 , w którym kąty wewnętrzne mają odpowiednio miary:
, w którym kąty wewnętrzne mają odpowiednio miary: 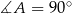 ,
, 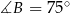 ,
, 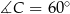 ,
, 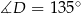 , a boki
, a boki 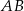 i
i 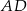 mają długość 3 cm. Sporządź rysunek pomocniczy.
mają długość 3 cm. Sporządź rysunek pomocniczy.
Oblicz pole rombu 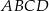 , wiedząc, że długości promieni okręgów opisanych na trójkątach
, wiedząc, że długości promieni okręgów opisanych na trójkątach 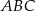 i
i 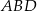 odpowiednio są równe
odpowiednio są równe 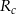 i
i 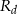 .
.
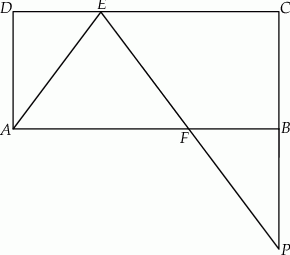
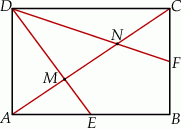
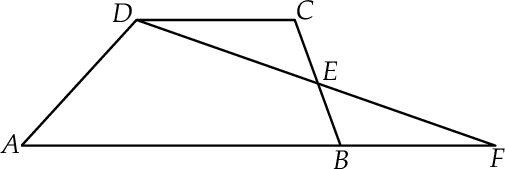
W trapezie 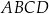 punkt
punkt 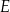 jest środkiem boku
jest środkiem boku 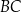 oraz
oraz 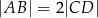 . Z wierzchołka
. Z wierzchołka 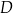 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 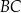 w punkcie
w punkcie 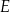 . Proste
. Proste 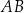 i
i 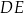 przecinają się w punkcie
przecinają się w punkcie  (zobacz rysunek).
(zobacz rysunek).
Wykaż, pole trójkąta 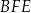 jest pięć razy mniejsze od pola czworokąta
jest pięć razy mniejsze od pola czworokąta 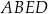 .
.

