W trapez 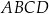 wpisano okrąg o środku
wpisano okrąg o środku 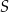 . Okrąg ten jest styczny do ramion
. Okrąg ten jest styczny do ramion 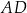 i
i 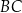 tego trapezu w punktach odpowiednio
tego trapezu w punktach odpowiednio 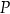 i
i 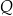 (zobacz rysunek).
(zobacz rysunek).

Uzasadnij, że trójkąt 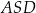 jest prostokątny. Wykaż, że
jest prostokątny. Wykaż, że 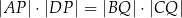 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trapez 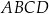 wpisano okrąg o środku
wpisano okrąg o środku 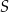 . Okrąg ten jest styczny do ramion
. Okrąg ten jest styczny do ramion 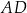 i
i 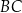 tego trapezu w punktach odpowiednio
tego trapezu w punktach odpowiednio 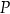 i
i 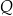 (zobacz rysunek).
(zobacz rysunek).

Uzasadnij, że trójkąt 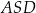 jest prostokątny. Wykaż, że
jest prostokątny. Wykaż, że 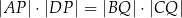 .
.
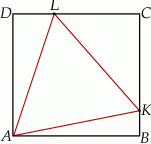
W prostokąt 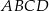 wpisany jest trójkąt równoboczny
wpisany jest trójkąt równoboczny 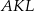 (patrz rysunek). Wierzchołek
(patrz rysunek). Wierzchołek 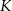 leży na boku
leży na boku 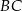 (
(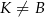 i
i 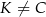 ), wierzchołek
), wierzchołek 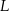 leży na boku
leży na boku 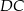 (
(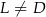 i
i 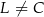 ). Udowodnij, że pole powierzchni trójkąta
). Udowodnij, że pole powierzchni trójkąta 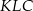 równe jest sumie pól trójkątów
równe jest sumie pól trójkątów 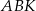 i
i 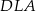 .
.
Dany jest prostokąt 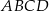 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 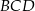 jest styczny do przekątnej
jest styczny do przekątnej 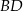 w punkcie
w punkcie 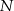 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 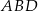 jest styczny do boku
jest styczny do boku 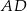 w punkcie
w punkcie 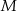 , a środek
, a środek 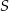 tego okręgu leży na odcinku
tego okręgu leży na odcinku 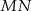 , jak na rysunku.
, jak na rysunku.
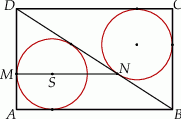
Wykaż, że 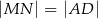 .
.
W czworokącie wypukłym  kąty przy wierzchołkach
kąty przy wierzchołkach  i
i  są proste (zobacz rysunek).
są proste (zobacz rysunek).
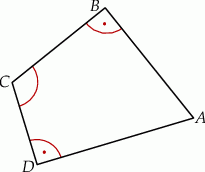
Oblicz sinus kąta przy wierzchołku 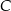 jeżeli
jeżeli 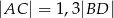 .
.
Sinus kąta jaki tworzą przekątne prostokąta o polu 60 jest równy 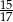 . Oblicz obwód tego prostokąta.
. Oblicz obwód tego prostokąta.
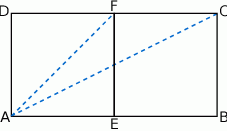
Odcinek 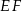 łączący środki dwóch dłuższych boków prostokąta
łączący środki dwóch dłuższych boków prostokąta  dzieli go na dwa kwadraty, przy czym przekątna prostokąta jest o 3 dłuższa od przekątnej kwadratu. Oblicz pole prostokąta
dzieli go na dwa kwadraty, przy czym przekątna prostokąta jest o 3 dłuższa od przekątnej kwadratu. Oblicz pole prostokąta  .
.
W deltoidzie 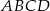 dane są
dane są  i
i  (zobacz rysunek). Oblicz pole tego deltoidu.
(zobacz rysunek). Oblicz pole tego deltoidu.
Kąt ostry równoległoboku ma miarę 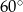 . Stosunek kwadratów długości przekątnych jest równy
. Stosunek kwadratów długości przekątnych jest równy 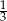 . Wykaż, że ten równoległobok jest rombem.
. Wykaż, że ten równoległobok jest rombem.
W trapezie prostokątnym 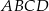 dłuższe ramię ma długość 10. Obwód tego trapezu jest równy 30. Wiedząc, że tangens kąta ostrego w trapezie
dłuższe ramię ma długość 10. Obwód tego trapezu jest równy 30. Wiedząc, że tangens kąta ostrego w trapezie 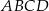 jest równy
jest równy 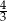 , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
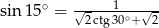
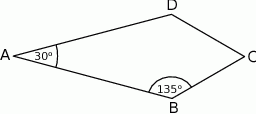
 dane są miary kątów
dane są miary kątów 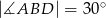 i
i 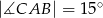 . Oblicz miarę kąta
. Oblicz miarę kąta 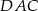 .
.W trapez równoramienny o obwodzie 60 wpisano okrąg. Przekątna trapezu ma długość 17. Oblicz pole trapezu.
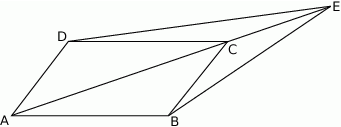
Dany jest równoległobok 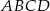 . Na przedłużeniu przekątnej
. Na przedłużeniu przekątnej 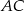 wybrano punkt
wybrano punkt 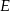 tak, że
tak, że 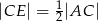 (zobacz rysunek). Uzasadnij, że pole równoległoboku
(zobacz rysunek). Uzasadnij, że pole równoległoboku 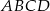 jest cztery razy większe od pola trójkąta
jest cztery razy większe od pola trójkąta 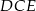 .
.
Na przekątnej  równoległoboku
równoległoboku  wybrano punkt
wybrano punkt  (zobacz rysunek). Uzasadnij, że trójkąty
(zobacz rysunek). Uzasadnij, że trójkąty 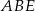 i
i 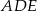 mają równe pola.
mają równe pola.
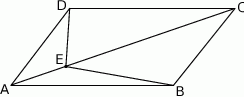
Pole prostokąta jest równe 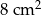 . Wyznacz jeden z boków prostokąta, jako funkcję drugiego boku i naszkicuj wykres tej funkcji. Podaj dziedzinę i zbiór wartości tej funkcji.
. Wyznacz jeden z boków prostokąta, jako funkcję drugiego boku i naszkicuj wykres tej funkcji. Podaj dziedzinę i zbiór wartości tej funkcji.
Punkt 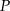 jest punktem przecięcia przekątnych trapezu
jest punktem przecięcia przekątnych trapezu 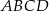 . Długość podstawy
. Długość podstawy 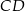 jest o 2 mniejsza od długości podstawy
jest o 2 mniejsza od długości podstawy 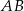 . Promień okręgu opisanego na trójkącie ostrokątnym
. Promień okręgu opisanego na trójkącie ostrokątnym 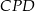 jest o 3 mniejszy od promienia okręgu opisanego na trójkącie
jest o 3 mniejszy od promienia okręgu opisanego na trójkącie 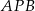 . Wykaż, że spełniony jest warunek
. Wykaż, że spełniony jest warunek 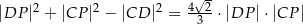 .
.
Dany jest czworokąt 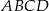 , w którym
, w którym 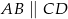 . Na boku
. Na boku 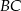 wybrano taki punkt
wybrano taki punkt 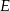 , że
, że 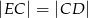 i
i 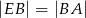 . Wykaż, że kąt
. Wykaż, że kąt 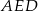 jest prosty.
jest prosty.
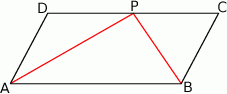
W równoległoboku 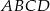 środek
środek  boku
boku 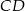 połączono odcinkami z wierzchołkami
połączono odcinkami z wierzchołkami 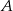 i
i 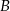 . Wiadomo, że
. Wiadomo, że 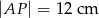 i
i 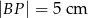 oraz
oraz 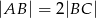 . Oblicz obwód równoległoboku.
. Oblicz obwód równoległoboku.
Obwód rombu wynosi 18 cm, a jego pole 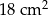 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
Na okręgu o promieniu  opisano trapez prostokątny, którego najkrótszy bok ma długość
opisano trapez prostokątny, którego najkrótszy bok ma długość 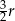 . Oblicz pole tego trapezu oraz stosunek długości jego przekątnych.
. Oblicz pole tego trapezu oraz stosunek długości jego przekątnych.
W trapez prostokątny wpisano okrąg o promieniu  . Najkrótszy bok tego trapezu ma długość
. Najkrótszy bok tego trapezu ma długość 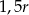 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Dwa przeciwległe boki czworokąta wpisanego w okrąg mają równe długości. Wykaż, że czworokąt ten jest trapezem.
Dany jest czworokąt wypukły 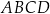 . Przekątne
. Przekątne 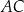 oraz
oraz 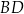 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 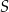 . Wykaż, że jeżeli
. Wykaż, że jeżeli 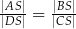 , to na czworokącie
, to na czworokącie 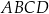 można opisać okrąg.
można opisać okrąg.
