Podstawy trapezu prostokątnego mają długości 5 i 9 oraz cosinus kąta ostrego jest równy 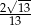 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Pole kwadratu 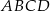 jest równe 16. Punkt
jest równe 16. Punkt  jest środkiem boku
jest środkiem boku  , a punkt
, a punkt 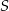 punktem przecięcia przekątnej
punktem przecięcia przekątnej 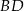 kwadratu i odcinka
kwadratu i odcinka 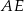 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 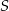 od boku
od boku 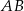 jest równa
jest równa 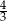 .
.
Na okręgu o średnicy 8 opisano trapez prostokątny, w którym jedna z podstaw ma długość 15. Oblicz pole tego trapezu.
Stosunek długości boków trapezu równoramiennego wynosi 17:13:7:13. Oblicz obwód trapezu wiedząc, że jego pole jest równe 36.
Boki równoległoboku mają długości 6 i 14, a jego krótsza przekątna ma długość 11. Oblicz cosinus kąta rozwartego tego równoległoboku.
O ile centymetrów należy przedłużyć długość i szerokość prostokąta o wymiarach 8 cm na 5 cm aby jego pole zwiększyło się o 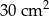 ?
?
W czworokąt 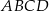 , w którym
, w którym 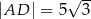 i
i 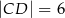 , można wpisać okrąg. Przekątna
, można wpisać okrąg. Przekątna 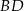 tworzy z bokiem
tworzy z bokiem 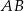 czworokąta kąt o mierze
czworokąta kąt o mierze 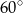 , natomiast z bokiem
, natomiast z bokiem 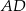 tworzy kąt, którego sinus jest równy
tworzy kąt, którego sinus jest równy  . Wyznacz długości boków
. Wyznacz długości boków 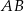 i
i 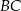 oraz długość przekątnej
oraz długość przekątnej 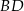 tego czworokąta.
tego czworokąta.
Przekątna 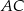 czworokąta
czworokąta 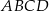 tworzy z bokiem
tworzy z bokiem 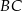 kąt
kąt 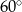 , a z bokiem
, a z bokiem 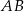 kąt
kąt 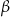 taki, że
taki, że 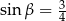 . Promień okręgu opisanego na trójkącie
. Promień okręgu opisanego na trójkącie 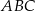 ma długość 5, a bok
ma długość 5, a bok 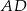 długość
długość 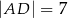 . Wiedząc, że w czworokąt
. Wiedząc, że w czworokąt 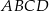 można wpisać okrąg oblicz długości pozostałych boków czworokąta oraz długość przekątnej
można wpisać okrąg oblicz długości pozostałych boków czworokąta oraz długość przekątnej 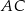 .
.
Na okręgu jest opisany czworokąt 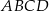 . Bok
. Bok 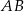 tego czworokąta jest trzy razy krótszy od przekątnej
tego czworokąta jest trzy razy krótszy od przekątnej 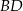 , a bok
, a bok 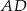 ma długość 10. Ponadto spełnione są następujące warunki:
ma długość 10. Ponadto spełnione są następujące warunki:
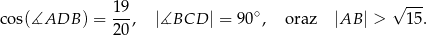
Oblicz długość boku 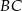 tego czworokąta.
tego czworokąta.
W czworokąt 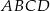 , w którym
, w którym 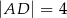 i
i 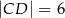 , można wpisać okrąg. Przekątna
, można wpisać okrąg. Przekątna 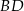 tworzy z bokiem
tworzy z bokiem 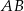 czworokąta kąt o mierze
czworokąta kąt o mierze 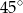 , natomiast z bokiem
, natomiast z bokiem 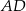 tworzy kąt, którego sinus jest równy
tworzy kąt, którego sinus jest równy 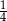 . Wyznacz długości boków
. Wyznacz długości boków 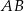 i
i 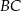 oraz długość przekątnej
oraz długość przekątnej 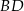 tego czworokąta.
tego czworokąta.
Na okręgu jest opisany czworokąt 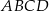 . Bok
. Bok 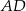 tego czworokąta jest dwa razy dłuższy od boku
tego czworokąta jest dwa razy dłuższy od boku 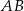 , a przekątna
, a przekątna 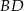 ma długość równą 6. Ponadto spełnione są następujące warunki:
ma długość równą 6. Ponadto spełnione są następujące warunki:
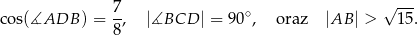
Oblicz długość boku 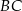 tego czworokąta.
tego czworokąta.
Trapez równoramienny o obwodzie 20 dm i przekątnej długości 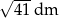 jest opisany na okręgu. Oblicz jego pole i cosinusy jego kątów wewnętrznych.
jest opisany na okręgu. Oblicz jego pole i cosinusy jego kątów wewnętrznych.
Boki prostokąta 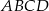 mają długości
mają długości 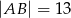 i
i 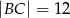 . Punkt
. Punkt 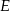 jest punktem boku
jest punktem boku 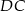 takim, że
takim, że 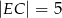 , a punkt
, a punkt 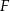 jest takim punktem odcinka
jest takim punktem odcinka 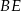 , że
, że 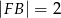 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 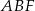 .
.
Na trapezie równoramiennym o podstawach 2 i 6 opisano okrąg. Oblicz pole trapezu, jeśli dłuższa podstawa jest średnicą tego okręgu.
Na bokach 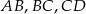 i
i 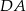 czworokąta
czworokąta 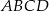 wybrano punkty
wybrano punkty 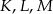 i
i 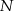 takie, że
takie, że
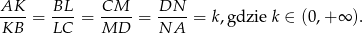
Oblicz stosunek pola czworokąta 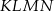 do pola czworokąta
do pola czworokąta 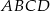 .
.
W trapezie równoramiennym, którego podstawy mają długość  i
i 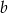 (
(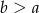 ), kąt ostry ma miarę
), kąt ostry ma miarę  , połączono odcinkami środki sąsiednich boków. Oblicz pole powstałego czworokąta.
, połączono odcinkami środki sąsiednich boków. Oblicz pole powstałego czworokąta.
W trapezie prostokątnym różnica długości podstaw jest równa 4,5 cm, a tangens kąta ostrego wynosi 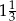 . Oblicz różnicę długości ramion tego trapezu.
. Oblicz różnicę długości ramion tego trapezu.
Oblicz długość boku rombu wiedząc, że prosta poprowadzona przez jeden z jego wierzchołków odcina na przedłużeniach dwóch jego boków odcinki o długościach 4 i 9.
Na okręgu o promieniu  opisano trapez równoramienny, którego kąt ostry ma miarę
opisano trapez równoramienny, którego kąt ostry ma miarę  . Wykaż, że promień okręgu opisanego na tym czworokącie jest równy
. Wykaż, że promień okręgu opisanego na tym czworokącie jest równy 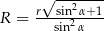 .
.
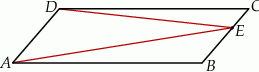
Na rysunku przedstawiono równoległobok  i trójkąt
i trójkąt 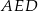 . Punkt
. Punkt 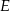 leży na odcinku
leży na odcinku 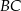 . Uzasadnij, że pole równoległoboku
. Uzasadnij, że pole równoległoboku 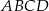 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 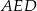 .
.
Przekątne rombu  przecinają się w punkcie
przecinają się w punkcie  . Punkt
. Punkt 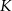 jest takim punktem boku
jest takim punktem boku 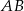 , że odcinek
, że odcinek 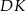 jest wysokością rombu (zobacz rysunek).
jest wysokością rombu (zobacz rysunek).
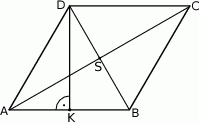
Wykaż, że jeżeli trójkąty 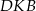 i
i 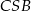 są przystające, to punkt
są przystające, to punkt 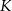 jest środkiem odcinka
jest środkiem odcinka 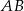 .
.
Czworokąt 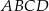 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 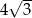 (patrz rysunek). Przekątna
(patrz rysunek). Przekątna 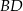 czworokąta ma długość 12. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta jest równy
czworokąta ma długość 12. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta jest równy 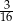 . Wiedząc, że
. Wiedząc, że 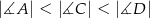 , oblicz miary kątów czworokąta
, oblicz miary kątów czworokąta 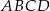 .
.
Czworokąt 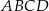 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 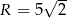 . Przekątna
. Przekątna 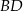 tego czworokąta ma długość 10. Kąty wewnętrzne
tego czworokąta ma długość 10. Kąty wewnętrzne 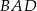 i
i 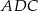 czworokąta
czworokąta 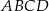 są ostre, a iloczyn sinusów wszystkich jego kątów wewnętrznych jest równy
są ostre, a iloczyn sinusów wszystkich jego kątów wewnętrznych jest równy  . Oblicz miary kątów wewnętrznych tego czworokąta.
. Oblicz miary kątów wewnętrznych tego czworokąta.
W równoległoboku o obwodzie równym 144, wysokości 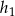 i
i 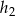 spełniają warunek
spełniają warunek 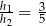 . Oblicz długości boków tego równoległoboku.
. Oblicz długości boków tego równoległoboku.
W równoległoboku o obwodzie równym 96 cm stosunek wysokości jest równy 5:7. Oblicz długości boków tego równoległoboku.
Kąt ostry równoległoboku ma miarę 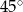 . Punkt wspólny przekątnych równoległoboku jest oddalony od boków o
. Punkt wspólny przekątnych równoległoboku jest oddalony od boków o 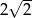 i 2. Oblicz pole równoległoboku oraz długości jego przekątnych.
i 2. Oblicz pole równoległoboku oraz długości jego przekątnych.

