Bok rombu ma długość 6, a sinus kąta ostrego tego rombu jest równy 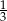 . Oblicz pole rombu.
. Oblicz pole rombu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Wykaż, że środki boków rombu są wierzchołkami prostokąta.
Oblicz pole równoległoboku o bokach 7 cm i 12 cm, w którym dwa sąsiednie kąty różnią się o 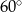 .
.
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku. Jaka figurę otrzymamy, łącząc kolejno środki boków: a) rombu, b) prostokąta, c) kwadratu?
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
W trapezie 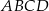 punkt
punkt 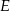 jest środkiem ramienia
jest środkiem ramienia 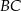 . Z wierzchołka
. Z wierzchołka 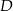 poprowadzono prostą przecinającą ramię
poprowadzono prostą przecinającą ramię 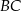 w punkcie
w punkcie 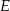 . Proste
. Proste 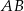 i
i 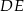 przecinają się w punkcie
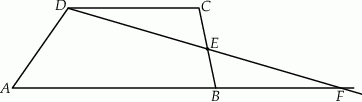
przecinają się w punkcie 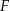 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 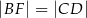 .
.
Na bokach 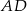 i
i 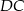 kwadratu
kwadratu 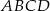 o polu 1 wybrano punkty
o polu 1 wybrano punkty 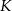 i
i 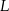 w ten sposób, że
w ten sposób, że 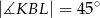 .
.
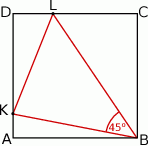
Oblicz odległość punktu 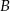 od prostej
od prostej 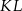 .
.
Dany jest trapez o podstawach długości  oraz
oraz 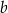 i wysokości
i wysokości 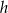 . Każdą z podstaw tego trapezu wydłużono o 25%, a wysokość skrócono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent skrócono wysokość
. Każdą z podstaw tego trapezu wydłużono o 25%, a wysokość skrócono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent skrócono wysokość 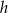 trapezu.
trapezu.
Dany jest trapez o podstawach długości  oraz
oraz 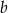 i wysokości
i wysokości 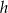 . Każdą z podstaw tego trapezu skrócono o 20%, a wysokość wydłużono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent wydłużono wysokość
. Każdą z podstaw tego trapezu skrócono o 20%, a wysokość wydłużono tak, że powstał nowy trapez o takim samym polu. Oblicz, o ile procent wydłużono wysokość 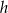 trapezu.
trapezu.
Trapez równoramienny 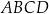 nie jest równoległobokiem. Przekątna
nie jest równoległobokiem. Przekątna 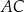 tego trapezu tworzy z podstawą
tego trapezu tworzy z podstawą 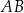 kąt o mierze
kąt o mierze 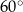 . Wykaż, że trapez
. Wykaż, że trapez 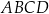 nie może być opisany na okręgu.
nie może być opisany na okręgu.
W trapezie równoramiennym przekątna ma długość 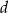 i tworzy z dłuższą podstawą kąt o mierze
i tworzy z dłuższą podstawą kąt o mierze  . Wykaż, że pole tego trapezu jest równe
. Wykaż, że pole tego trapezu jest równe 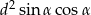 .
.
Punkty 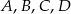 są kolejnymi wierzchołkami równoległoboku o obwodzie równym 26. Wiedząc, że kąt przy wierzchołku
są kolejnymi wierzchołkami równoległoboku o obwodzie równym 26. Wiedząc, że kąt przy wierzchołku 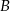 ma miarę
ma miarę 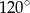 i promień okręgu wpisanego w trójkąt
i promień okręgu wpisanego w trójkąt 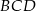 jest równy
jest równy 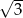 , oblicz długości boków i pole tego równoległoboku.
, oblicz długości boków i pole tego równoległoboku.
Oblicz długości boków trapezu równoramiennego opisanego na okręgu, znając obwód trapezu 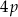 i długość
i długość 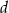 jego przekątnej.
jego przekątnej.
Przekątne rombu 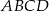 , o kącie ostrym przy wierzchołku
, o kącie ostrym przy wierzchołku 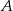 , mają długości 6cm i 8cm.
, mają długości 6cm i 8cm.
- Oblicz cosinus kąta
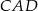 .
. - Wyznacz promień okręgu wpisanego w romb.
W trapezie 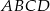 podstawa
podstawa 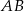 jest 3 razy dłuższa od podstawy
jest 3 razy dłuższa od podstawy 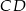 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 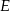 , a proste zawierające ramiona
, a proste zawierające ramiona 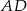 i
i 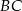 przecinają się w punkcie
przecinają się w punkcie 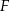 . Oblicz stosunek pola czworokąta
. Oblicz stosunek pola czworokąta 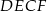 do pola trapezu
do pola trapezu 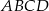 .
.
Ramiona trapezu mają długości 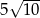 i 20. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
i 20. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
Trapez prostokątny o podstawach  i
i 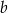 jest opisany na okręgu. Oblicz pole tego trapezu.
jest opisany na okręgu. Oblicz pole tego trapezu.
Czworokąt 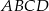 jest wpisany w okrąg oraz pola trójkątów
jest wpisany w okrąg oraz pola trójkątów 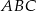 i
i 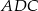 są równe. Wykaż, że
są równe. Wykaż, że
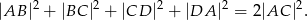
Dwa kwadraty 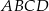 i
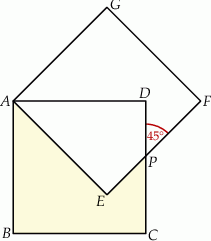
i 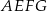 o boku długości 2 nałożono na siebie tak jak na rysunku poniżej. Oblicz pole pięciokąta
o boku długości 2 nałożono na siebie tak jak na rysunku poniżej. Oblicz pole pięciokąta 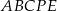 .
.
W romb o boku równym 8 i kącie ostrym równym 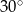 wpisano koło, a następnie w to koło wpisano kwadrat. Wyznacz stosunek pola rombu do pola kwadratu.
wpisano koło, a następnie w to koło wpisano kwadrat. Wyznacz stosunek pola rombu do pola kwadratu.
Dany jest kwadrat 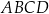 o boku długości 3. Punkty
o boku długości 3. Punkty 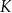 i
i 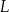 leżą na prostych – odpowiednio –
leżą na prostych – odpowiednio – 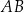 i
i 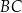 tak, że
tak, że 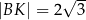 i
i 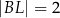 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 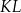 przecina przekątną
przecina przekątną 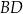 tego kwadratu w punkcie
tego kwadratu w punkcie 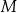 .
.
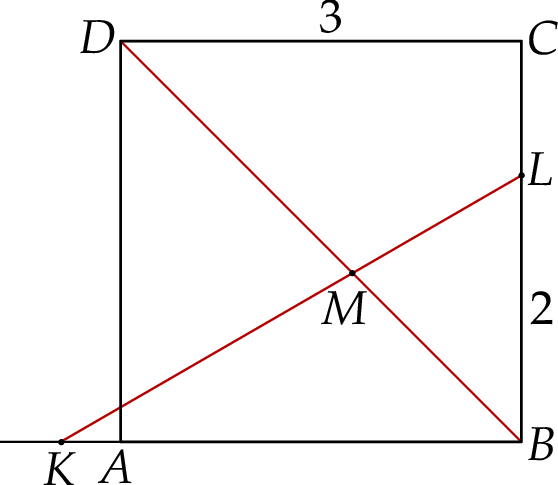
Wykaż, że 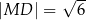 .
.
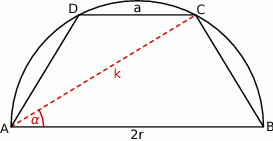
W półkole o promieniu  wpisano trapez równoramienny. Przekątna trapezu o długości
wpisano trapez równoramienny. Przekątna trapezu o długości 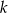 tworzy z dłuższą podstawą kąt o mierze
tworzy z dłuższą podstawą kąt o mierze  , a krótsza podstawa trapezu ma długość
, a krótsza podstawa trapezu ma długość  . Uzasadnij, że
. Uzasadnij, że 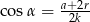 .
.