Trapez prostokątny 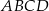 o podstawach
o podstawach 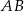 i
i 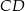 jest opisany na okręgu. Ramię
jest opisany na okręgu. Ramię 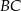 ma długość 10, a ramię
ma długość 10, a ramię 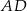 jest wysokością trapezu. Podstawa
jest wysokością trapezu. Podstawa 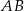 jest 2 razy dłuższa od podstawy
jest 2 razy dłuższa od podstawy 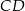 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Trapez prostokątny 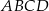 o podstawach
o podstawach 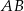 i
i 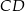 jest opisany na okręgu. Ramię
jest opisany na okręgu. Ramię 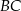 ma długość 15, a ramię
ma długość 15, a ramię 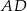 jest wysokością trapezu. Podstawa
jest wysokością trapezu. Podstawa 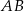 jest 3 razy dłuższa od podstawy
jest 3 razy dłuższa od podstawy 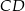 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Podstawy trapezu mają długości  i
i 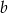 (
(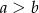 ). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi
). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi 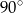 . Oblicz długość odcinka łączącego środki podstaw trapezu.
. Oblicz długość odcinka łączącego środki podstaw trapezu.
W prostokącie przekątna o długości 1,53 cm tworzy z dłuższym bokiem kąt o mierze 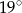 . Oblicz z dokładnością do
. Oblicz z dokładnością do 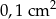 pole prostokąta.
pole prostokąta.
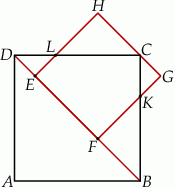
Bok 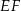 kwadratu
kwadratu 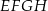 zawiera się w przekątnej
zawiera się w przekątnej 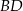 kwadratu
kwadratu 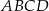 , a punkt
, a punkt 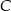 należy do odcinka
należy do odcinka 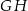 . Odcinki
. Odcinki 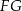 i
i 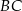 przecinają się w punkcie
przecinają się w punkcie 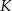 , a odcinki
, a odcinki 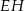 i
i 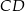 przecinają się w punkcie
przecinają się w punkcie 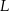 . Wykaż, że
. Wykaż, że 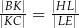 .
.
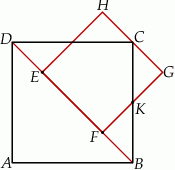
Bok 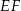 kwadratu
kwadratu 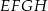 zawiera się w przekątnej
zawiera się w przekątnej 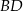 kwadratu
kwadratu 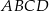 , a punkt
, a punkt 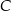 jest środkiem odcinka
jest środkiem odcinka 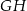 . Odcinki
. Odcinki 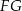 i
i 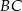 przecinają się w punkcie
przecinają się w punkcie 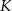 . Wykaż, że
. Wykaż, że 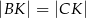 .
.
Pole równoległoboku jest równe 24. Stosunek jego wysokości jest równy 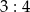 . Długości boków wyrażają się liczbami naturalnymi, a długość każdej z wysokości jest mniejsza od 5 i większa od 2. Oblicz długości boków równoległoboku.
. Długości boków wyrażają się liczbami naturalnymi, a długość każdej z wysokości jest mniejsza od 5 i większa od 2. Oblicz długości boków równoległoboku.
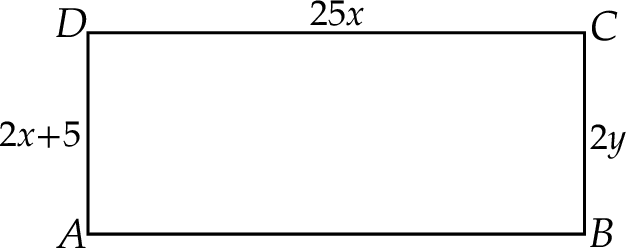
Wyznacz pole narysowanego prostokąta, jeżeli 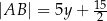 .
.
Dwusieczne kątów 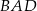 i
i 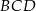 czworokąta wypukłego
czworokąta wypukłego 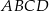 przecinają się w punkcie
przecinają się w punkcie 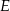 , przy czym punkty
, przy czym punkty 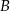 i
i 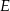 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 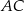 (zobacz rysunek).
(zobacz rysunek).
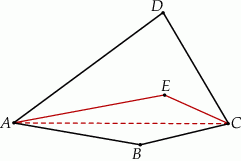
Wykaż, że 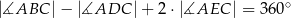 .
.
Przekątne rombu mają długość 8 cm i 13 cm. Oblicz pole czworokąta, którego wierzchołkami są środki boków romb.
Podstawy trapezu mają długości 6 i 2, a wysokość ma długość 4. Oblicz odległość punktu przecięcia przekątnych trapezu od prostych zawierających jego podstawy.
W trapezie równoramiennym 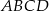 , w którym
, w którym 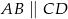 , dane są
, dane są 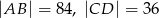 ,
, 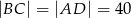 . Oblicz promień okręgu wpisanego w trójkąt
. Oblicz promień okręgu wpisanego w trójkąt 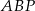 , gdzie
, gdzie 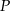 jest punktem przecięcia przekątnych tego trapezu.
jest punktem przecięcia przekątnych tego trapezu.
W kwadrat wpisano drugi kwadrat, którego wierzchołki leżą na bokach pierwszego i boki tworzą z bokami pierwszego kwadratu kąty o miarach 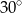 . Jaką częścią pola dużego kwadratu jest pole małego kwadratu?
. Jaką częścią pola dużego kwadratu jest pole małego kwadratu?
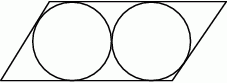
W równoległoboku wpisano dwa przystające okręgi styczne zewnętrznie do siebie (patrz rysunek). Wykaż, że średnica każdego z tych okręgów jest równa różnicy długości dłuższego i krótszego boku tego równoległoboku.
Podstawy trapezu 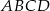 mają długości
mają długości 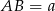 i
i 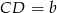 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 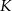 i
i 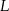 w ten sposób, że odcinek
w ten sposób, że odcinek 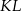 jest równoległy do podstaw oraz
jest równoległy do podstaw oraz 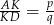 . Oblicz długość odcinka
. Oblicz długość odcinka 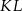 .
.
Wykaż, że stosunek pola kwadratu wpisanego w koło do pola tego koła jest mniejszy od  .
.
Wykaż, że stosunek pola kwadratu opisanego na kole do pola tego koła jest mniejszy od 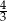 .
.
Pola dwóch kwadratów różnią się o 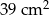 . Przekątna jednego z nich jest dłuższa o
. Przekątna jednego z nich jest dłuższa o 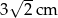 od przekątnej drugiego. Oblicz długość boku każdego kwadratu.
od przekątnej drugiego. Oblicz długość boku każdego kwadratu.
Pole trapezu prostokątnego opisanego na okręgu jest równe 5, a obwód trapezu wynosi 10. Oblicz długość promienia okręgu.
W kwadrat o boku 2 wpisano drugi kwadrat w ten sposób, że bok wpisanego kwadratu tworzy z bokiem danego kąt 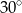 . Oblicz długość krótszego z odcinków łączących wierzchołki tych kwadratów.
. Oblicz długość krótszego z odcinków łączących wierzchołki tych kwadratów.
W trapez można wpisać okrąg o promieniu 4 i jednocześnie na tym trapezie można opisać okrąg. Kąt ostry trapezu ma miarę 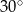 . Oblicz promień okręgu opisanego na tym trapezie.
. Oblicz promień okręgu opisanego na tym trapezie.
W dany trapez można wpisać okrąg i jednocześnie można na tym trapezie opisać okrąg. Wysokość tego trapezu jest równa 8, a jego kąt ostry ma miarę 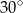 . Oblicz długość promienia okręgu opisanego na tym trapezie.
. Oblicz długość promienia okręgu opisanego na tym trapezie.
Punkt 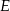 jest środkiem boku
jest środkiem boku 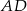 równoległoboku
równoległoboku 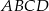 . Pole trójkąta
. Pole trójkąta 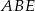 jest równe 2. Oblicz pole równoległoboku.
jest równe 2. Oblicz pole równoległoboku.
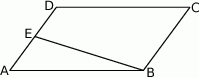
W trapezie 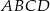 ramiona mają długości
ramiona mają długości 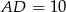 oraz
oraz 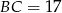 , zaś tangens kąta nachylenia ramienia
, zaś tangens kąta nachylenia ramienia 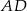 do dłuższej podstawy
do dłuższej podstawy 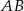 wynosi
wynosi 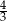 . Wiedząc, że w dany trapez można wpisać okrąg oblicz
. Wiedząc, że w dany trapez można wpisać okrąg oblicz
- pole trapezu,
- pole trójkąta
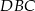 .
.

