Suma długości boku kwadratu i jego przekątnej jest równa 1. Oblicz długość przekątnej kwadratu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Różnica między długością przekątnej kwadratu i długością jego boku wynosi 2 cm. Oblicz długość boku tego kwadratu.
Różnica między długością przekątnej kwadratu i długością jego boku wynosi 1 cm. Oblicz długość boku tego kwadratu.
Przekątna kwadratu jest o 1 dłuższa od jego boku. Oblicz pole i obwód tego kwadratu.
Na czworokącie wypukłym 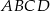 , w którym
, w którym 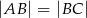 ,
, 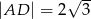 ,
, 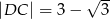 można opisać okrąg. Wiedząc, że przekątna
można opisać okrąg. Wiedząc, że przekątna 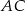 ma długość
ma długość 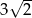 , oblicz pole tego czworokąta.
, oblicz pole tego czworokąta.
Punkt 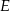 jest środkiem boku
jest środkiem boku 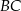 równoległoboku
równoległoboku 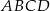 , a odcinek
, a odcinek  przecina przekątną
przecina przekątną 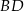 w punkcie
w punkcie 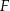 . Wykaż, że
. Wykaż, że 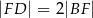 .
.
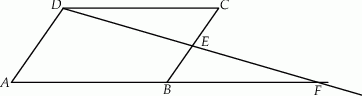
W równoległoboku 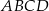 punkt
punkt 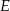 jest środkiem boku
jest środkiem boku 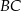 . Z wierzchołka
. Z wierzchołka 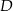 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 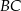 w punkcie
w punkcie 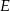 . Proste
. Proste 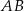 i
i 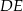 przecinają się w punkcie
przecinają się w punkcie 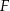 (zobacz rysunek). Wykaż, że punkt
(zobacz rysunek). Wykaż, że punkt 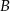 jest środkiem odcinka
jest środkiem odcinka 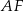 .
.
Kąt ostry równoległoboku ma miarę 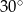 . Odległości punktu przecięcia przekątnych równoległoboku od prostych zawierających jego boki są równe 2 oraz 6 odpowiednio. Oblicz pole równoległoboku i długość jego krótszej przekątnej.
. Odległości punktu przecięcia przekątnych równoległoboku od prostych zawierających jego boki są równe 2 oraz 6 odpowiednio. Oblicz pole równoległoboku i długość jego krótszej przekątnej.
Obwód równoległoboku 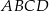 jest równy 26, miara jego kąta rozwartego
jest równy 26, miara jego kąta rozwartego 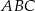 jest równa
jest równa 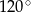 , a promień okręgu wpisanego w trójkąt
, a promień okręgu wpisanego w trójkąt 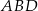 jest równy
jest równy 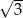 . Oblicz długości boków równoległoboku
. Oblicz długości boków równoległoboku 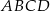 .
.
Wysokości równoległoboku mają długości 2 i 4. Oblicz pole równoległoboku wiedząc, że jego obwód wynosi 30.
Wysokości równoległoboku o obwodzie 20 cm mają długości 2 cm i 3 cm. Oblicz pole równoległoboku.
Wysokości równoległoboku o obwodzie 18 cm mają długości 2 cm i 4 cm. Oblicz pole równoległoboku.
W trapezie 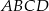 , w którym
, w którym 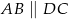 oraz
oraz 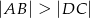 , przekątna
, przekątna 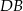 zawiera się w dwusiecznej kąta
zawiera się w dwusiecznej kąta 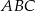 . Wykaż, że
. Wykaż, że 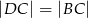 .
.
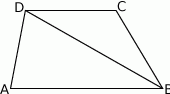
Punkt 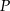 leży wewnątrz prostokąta
leży wewnątrz prostokąta 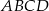 . Wykaż, że suma pól trójkątów
. Wykaż, że suma pól trójkątów 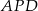 i
i 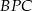 jest równa sumie pól trójkątów
jest równa sumie pól trójkątów 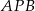 i
i 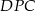 .
.
Dany jest trapez prostokątny 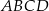 o podstawach
o podstawach 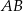 i
i 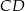 oraz wysokości
oraz wysokości 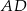 . Dwusieczna kąta
. Dwusieczna kąta 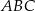 przecina ramię
przecina ramię 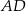 w punkcie
w punkcie 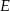 oraz dwusieczną kąta
oraz dwusieczną kąta 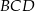 w punkcie
w punkcie 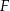 (zobacz rysunek).
(zobacz rysunek).
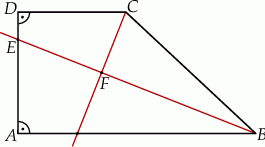
Wykaż, że w czworokącie 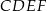 sumy miar przeciwległych kątów są sobie równe.
sumy miar przeciwległych kątów są sobie równe.
Znaleźć kąt ostry rombu, jeżeli wiadomo, że jego pole jest równe 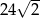 , a promień okręgu w niego wpisanego równy
, a promień okręgu w niego wpisanego równy 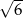 .
.
Na okręgu opisano trapez, w którym krótsza podstawa ma długość  , a dłuższa podstawa tworzy z ramionami kąty o mierze
, a dłuższa podstawa tworzy z ramionami kąty o mierze  . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Na bokach 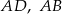 i
i 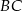 rombu
rombu 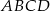 wybrano punkty
wybrano punkty 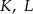 i
i 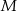 w ten sposób, że
w ten sposób, że 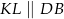 i
i 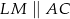 . Uzasadnij, że pole czworokąta
. Uzasadnij, że pole czworokąta  stanowi połowę pola rombu.
stanowi połowę pola rombu.
Długości boków prostokąta są równe 3 oraz 5. Oblicz sinus kąta ostrego, który tworzą przekątne tego prostokąta.
Długości boków prostokąta są równe 8 oraz 15. Oblicz cosinus kąta rozwartego, który tworzą przekątne tego prostokąta.
Wykaż, że stosunek długości promienia okręgu opisanego na kwadracie do długości promienia wpisanego w ten kwadrat jest równy 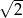 .
.
Wykaż, że stosunek długości promienia okręgu wpisanego w kwadrat do długości promienia okręgu opisanego na kwadracie jest równy 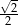 .
.
Promień koła wpisanego w trapez prostokątny jest równy  , kąt ostry trapezu równy jest
, kąt ostry trapezu równy jest  . Oblicz pole i obwód trapezu.
. Oblicz pole i obwód trapezu.
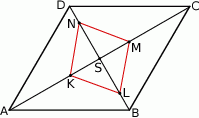
Przekątne rombu 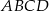 przecinają się w punkcie
przecinają się w punkcie 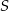 . Punkty
. Punkty 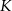 i
i 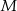 leżą na przekątnej
leżą na przekątnej 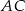 tak, że
tak, że 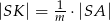 i
i 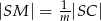 . Punkty
. Punkty 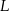 i
i 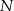 leżą na przekątnej
leżą na przekątnej 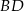 tak, że
tak, że 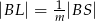 i
i 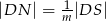 (zobacz rysunek). Wykaż, że jeżeli stosunek pola czworokąta
(zobacz rysunek). Wykaż, że jeżeli stosunek pola czworokąta 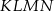 do pola rombu
do pola rombu 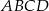 jest równy 1:4, to
jest równy 1:4, to 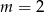 .
.
Czworokąt wypukły 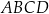 jest wpisany w okrąg o promieniu 4. Kąty
jest wpisany w okrąg o promieniu 4. Kąty 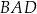 i
i 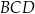 są proste (zobacz rysunek). Przekątne
są proste (zobacz rysunek). Przekątne 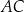 i
i 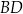 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 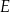 tak, że
tak, że 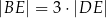 oraz
oraz 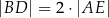 .
.

Oblicz długości boków czworokąta 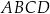 .
.
Czworokąt wypukły 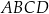 jest wpisany w okrąg o promieniu 9. Kąty
jest wpisany w okrąg o promieniu 9. Kąty 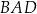 i
i 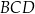 są proste (zobacz rysunek). Przekątne
są proste (zobacz rysunek). Przekątne 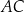 i
i 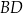 tego czworokąta przecinają się w punkcie
tego czworokąta przecinają się w punkcie 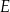 tak, że
tak, że  oraz
oraz 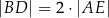 .
.

Oblicz długości boków czworokąta 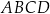 .
.
Punkty 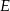 i
i 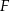 są środkami boków
są środkami boków 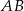 i
i 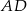 deltoidu
deltoidu 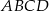 . Pole trójkąta
. Pole trójkąta 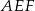 jest równe 3. Oblicz pole deltoidu
jest równe 3. Oblicz pole deltoidu 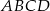 .
.
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
W trapezie prostokątnym krótsza przekątna ma długość ramienia trapezu i dzieli go na dwa trójkąty prostokątne. Dłuższa podstawa trapezu jest równa 6. Oblicz obwód tego trapezu.
Przekątne trapezu o podstawach długości 1 i 2 są prostopadłe. Oblicz sumę kwadratów długości przekątnych trapezu.

