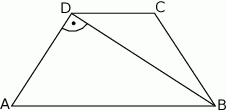
Dany jest czworokąt wypukły 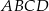 , w którym
, w którym 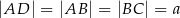 ,
, 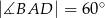 i
i 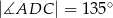 . Oblicz pole czworokąta
. Oblicz pole czworokąta 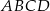 .
.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Boki 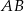 i
i 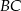 czworokąta
czworokąta 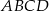 wpisanego w okrąg są równe przekątnej
wpisanego w okrąg są równe przekątnej 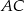 . Kąt
. Kąt 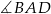 ma miarę
ma miarę 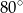 . Znajdź miary pozostałych kątów czworokąta
. Znajdź miary pozostałych kątów czworokąta 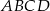 .
.
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
- Jeśli środki boków czworokąta wyznaczają prostokąt, czy można stwierdzić, że czworokąt jest rombem?
- Jeśli środki boków czworokąta wyznaczają romb, czy można stwierdzić, że czworokąt jest prostokątem?
- Jeśli środki boków czworokąta wyznaczają kwadrat, czy można stwierdzić, że czworokąt jest kwadratem?
W trapezie prostokątnym 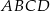 dłuższa podstawa
dłuższa podstawa 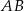 ma długość 8. Przekątna
ma długość 8. Przekątna 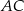 tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze
tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze 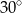 (zobacz rysunek). Oblicz długość przekątnej
(zobacz rysunek). Oblicz długość przekątnej 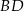 tego trapezu.
tego trapezu.
W trapezie prostokątnym 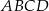 dłuższa podstawa
dłuższa podstawa 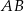 ma długość 15. Przekątna
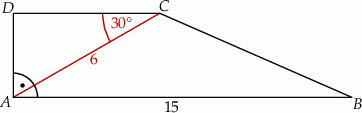
ma długość 15. Przekątna 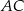 tego trapezu ma długość 6 i tworzy z krótszą podstawą trapezu kąt o mierze
tego trapezu ma długość 6 i tworzy z krótszą podstawą trapezu kąt o mierze 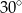 (zobacz rysunek). Oblicz długość przekątnej
(zobacz rysunek). Oblicz długość przekątnej 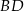 tego trapezu.
tego trapezu.
Dany jest trapez 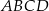 o podstawach
o podstawach 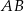 i
i 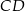 . Przekątne
. Przekątne 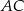 i
i 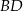 tego trapezu przecinają się w punkcie
tego trapezu przecinają się w punkcie 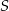 (zobacz rysunek) tak, że
(zobacz rysunek) tak, że 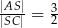 . Pole trójkąta
. Pole trójkąta 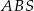 jest równe 12. Oblicz pole trójkąta
jest równe 12. Oblicz pole trójkąta 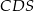 .
.
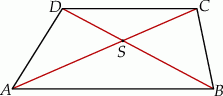
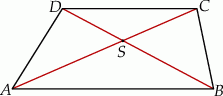
Dany jest trapez 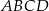 o podstawach
o podstawach 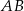 i
i 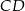 . Przekątne
. Przekątne 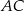 i
i 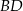 tego trapezu przecinają się w punkcie
tego trapezu przecinają się w punkcie 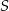 (zobacz rysunek) tak, że
(zobacz rysunek) tak, że 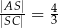 . Pole trójkąta
. Pole trójkąta 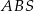 jest równe 24. Oblicz pole trójkąta
jest równe 24. Oblicz pole trójkąta 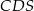 .
.
W równoległoboku 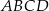 punkt
punkt 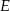 jest takim punktem boku
jest takim punktem boku 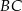 , że
, że 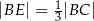 . Z wierzchołka
. Z wierzchołka 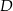 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 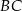 w punkcie
w punkcie 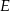 . Proste
. Proste 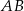 i
i 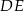 przecinają się w punkcie
przecinają się w punkcie 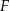 (zobacz rysunek). Wykaż, że pole trójkąta
(zobacz rysunek). Wykaż, że pole trójkąta 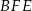 stanowi
stanowi 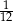 pola równoległoboku
pola równoległoboku 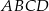 .
.
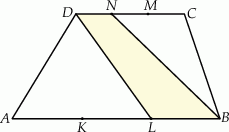
Punkty 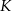 i
i 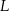 dzielą podstawę
dzielą podstawę 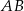 trapezu
trapezu 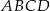 na trzy równe części, a punkty
na trzy równe części, a punkty 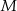 i
i 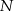 dzielą podstawę
dzielą podstawę 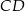 tego trapezu na trzy równe części. Pole czworokąta
tego trapezu na trzy równe części. Pole czworokąta 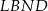 jest równe
jest równe 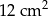 . Oblicz pole trapezu
. Oblicz pole trapezu 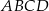 .
.
W trapezie równoramiennym 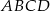 przekątna
przekątna 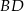 jest prostopadła do ramienia
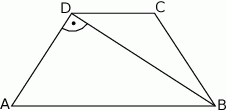
jest prostopadła do ramienia 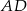 (zobacz rysunek). Podstawy trapezu mają długość:
(zobacz rysunek). Podstawy trapezu mają długość: 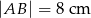 i
i 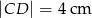 . Oblicz pole oraz miary kątów trapezu.
. Oblicz pole oraz miary kątów trapezu.
W trapezie równoramiennym 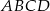 przekątna
przekątna 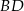 jest prostopadła do ramienia
jest prostopadła do ramienia 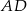 (zobacz rysunek). Podstawy trapezu mają długość:
(zobacz rysunek). Podstawy trapezu mają długość: 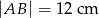 i
i 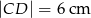 . Oblicz pole oraz miary kątów trapezu.
. Oblicz pole oraz miary kątów trapezu.
Dany jest prostokąt 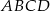 . Z wierzchołków
. Z wierzchołków 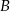 i
i 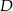 poprowadzono proste prostopadłe do przekątnej
poprowadzono proste prostopadłe do przekątnej 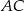 dzielące ją na trzy odcinki
dzielące ją na trzy odcinki 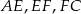 , każdy długości 4. Oblicz długość boków prostokąta.
, każdy długości 4. Oblicz długość boków prostokąta.
Na bokach 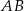 i
i 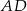 rombu
rombu 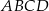 wybrano odpowiednio punkty
wybrano odpowiednio punkty 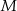 i
i 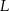 w ten sposób, że
w ten sposób, że 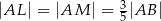 . Odcinek
. Odcinek 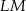 jest styczny do okręgu wpisanego w romb
jest styczny do okręgu wpisanego w romb 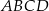 . Punkt
. Punkt 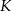 jest punktem styczności okręgu wpisanego w ten romb z bokiem
jest punktem styczności okręgu wpisanego w ten romb z bokiem 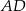 (zobacz rysunek).
(zobacz rysunek).
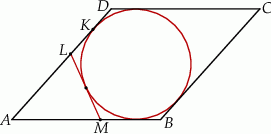
Wykaż, że 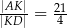 .
.
Dany jest trapez prostokątny 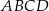 . Podstawa
. Podstawa 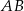 tego trapezu jest równa 26, a ramię
tego trapezu jest równa 26, a ramię 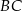 ma długość 24. Przekątna
ma długość 24. Przekątna 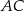 tego trapezu jest prostopadła do ramienia
tego trapezu jest prostopadła do ramienia 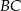 (zobacz rysunek).
(zobacz rysunek).
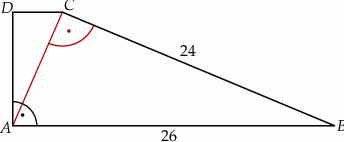
Oblicz długość ramienia 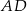 .
.
Oblicz pole i obwód trapezu prostokątnego, w którym podstawy mają długości 13 cm i 22 cm, a tangens kąta ostrego jest równy 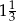 .
.
Przekątne trapezu 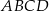 przecinają się w punkcie
przecinają się w punkcie 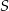 , jego podstawy mają długości
, jego podstawy mają długości 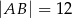 i
i 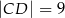 , a wysokość ma długość 8. Punkt
, a wysokość ma długość 8. Punkt 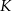 jest środkiem odcinka
jest środkiem odcinka 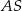 (zobacz rysunek).
(zobacz rysunek).
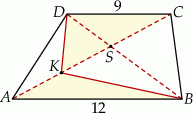
Oblicz stosunek pól trójkątów 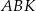 i
i 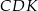 .
.
Przekątne trapezu 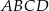 przecinają się w punkcie
przecinają się w punkcie 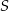 . Promień okręgu opisanego na trójkącie ostrokątnym
. Promień okręgu opisanego na trójkącie ostrokątnym 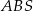 jest o 1 większy od promienia okręgu opisanego na trójkącie
jest o 1 większy od promienia okręgu opisanego na trójkącie 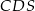 , a długości podstaw trapezu spełniają warunek
, a długości podstaw trapezu spełniają warunek 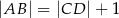 . Wykaż, że
. Wykaż, że
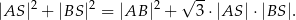
Czworokąt 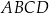 , w którym
, w którym 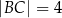 i
i 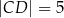 , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna 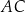 tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem 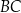 kąt o mierze
kąt o mierze 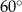 , natomiast z bokiem
, natomiast z bokiem 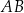 – kąt ostry, którego sinus jest równy
– kąt ostry, którego sinus jest równy  . Oblicz obwód czworokąta
. Oblicz obwód czworokąta 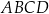 .
.
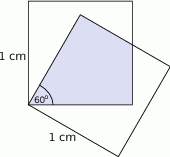
Kwadratowe szklane płytki o boku długości 1 cm, połączone w jednym wierzchołku, rozsunęły się tak, że boki wychodzące z jednego wierzchołka tworzą ze sobą kąt 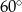 . Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do
. Oblicz pole części wspólnej płytek. Wynik podaj z dokładnością do 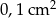 .
.
Oblicz pole trapezu równoramiennego o podstawach długości 10 cm i 6 cm oraz przekątnej o długości 9 cm.
W trapezie o podstawach długości 10 cm i 6 cm oraz wysokości równej 4 cm poprowadzono przekątne, które podzieliły go na cztery trójkąty. Oblicz pole każdego z otrzymanych trójkątów.
W trapezie o podstawach długości 12 cm i 8 cm oraz wysokości równej 6 cm poprowadzono przekątne, które podzieliły go na cztery trójkąty. Oblicz pole każdego z otrzymanych trójkątów.
Dany jest trapez 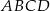 o podstawach
o podstawach 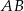 i
i 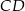 , w którym
, w którym 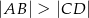 oraz ramię
oraz ramię 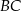 ma długość 6. Na tym trapezie opisano okrąg o promieniu
ma długość 6. Na tym trapezie opisano okrąg o promieniu 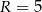 . Miary kątów
. Miary kątów 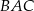 i
i 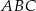 tego trapezu spełniają warunek
tego trapezu spełniają warunek
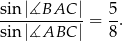
Oblicz pole i obwód trapezu 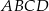 .
.
Czworokąt 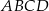 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 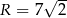 . Kąt
. Kąt 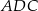 tego czworokąta jest ostry i jego miara jest o
tego czworokąta jest ostry i jego miara jest o 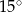 większa od miary kąta
większa od miary kąta 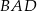 . Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta
. Iloczyn sinusów wszystkich kątów wewnętrznych czworokąta 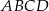 jest równy
jest równy  . Oblicz długości przekątnych
. Oblicz długości przekątnych 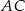 i
i 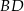 tego czworokąta.
tego czworokąta.

