Dłuższa przekątna równoległoboku o kącie ostrym 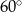 ma długość
ma długość 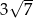 . Różnica długości jego boków wynosi 3. Oblicz pole tego równoległoboku i długość krótszej przekątnej.
. Różnica długości jego boków wynosi 3. Oblicz pole tego równoległoboku i długość krótszej przekątnej.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Przekątne czworokąta 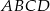 są prostopadłe.
są prostopadłe.
- Wykaż, że sumy kwadratów przeciwległych boków tego czworokąta są równe.
- Wykaż, że jeżeli długości jego boków
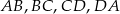 są kolejnymi wyrazami ciągu geometrycznego to czworokąt ten jest rombem.
są kolejnymi wyrazami ciągu geometrycznego to czworokąt ten jest rombem.
Wykaż, że jeżeli dwusieczne dwóch sąsiednich kątów wewnętrznych czworokąta wypukłego są prostopadłe, to czworokąt ten jest trapezem.
Kwadrat 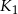 ma bok długości
ma bok długości  . Obok niego rysujemy kolejno kwadraty
. Obok niego rysujemy kolejno kwadraty 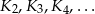 takie, że kolejny kwadrat ma bok o połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek).
takie, że kolejny kwadrat ma bok o połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek).
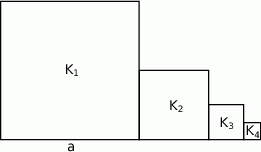
Wyznacz pole kwadratu 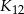 .
.
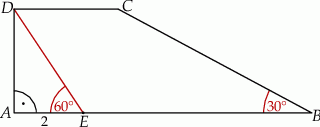
W trapezie prostokątnym 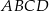 krótsze ramię
krótsze ramię 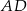 i krótsza podstawa
i krótsza podstawa 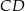 mają tę samą długość oraz
mają tę samą długość oraz 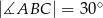 . Na podstawie
. Na podstawie 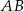 wybrano punkt
wybrano punkt 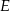 tak, że
tak, że 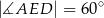 oraz
oraz 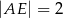 (zobacz rysunek). Oblicz długość odcinka
(zobacz rysunek). Oblicz długość odcinka 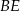 .
.
Na okręgu o promieniu 5 opisano deltoid o obwodzie 60. Oblicz pole deltoidu.
W czworokącie wypukłym 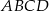 dane są:
dane są: 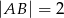 ,
, 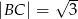 ,
, 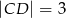 ,
, 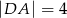 i
i 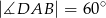 . Oblicz pole tego czworokąta.
. Oblicz pole tego czworokąta.
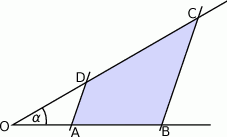
Wiedząc, że 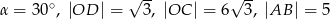 oraz
oraz 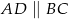 , oblicz pole i obwód trapezu
, oblicz pole i obwód trapezu  przedstawionego na rysunku.
przedstawionego na rysunku.
W równoległoboku 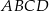 miara kąta ostrego jest równa
miara kąta ostrego jest równa 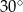 , a odległości punktu przecięcia się przekątnych od sąsiednich boków równoległoboku są równe 2 i
, a odległości punktu przecięcia się przekątnych od sąsiednich boków równoległoboku są równe 2 i 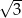 . Oblicz długość krótszej przekątnej tego równoległoboku.
. Oblicz długość krótszej przekątnej tego równoległoboku.
W trapezie równoramiennym 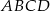 punkty
punkty 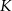 i
i 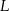 są odpowiednio środkami ramion
są odpowiednio środkami ramion 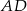 i
i 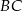 . Przekątna
. Przekątna 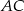 przecina odcinek
przecina odcinek 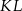 w punkcie
w punkcie 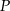 . Wiedząc, że
. Wiedząc, że 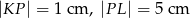 oraz wysokość trapezu jest równa 3 cm, oblicz długość boków trapezu.
oraz wysokość trapezu jest równa 3 cm, oblicz długość boków trapezu.
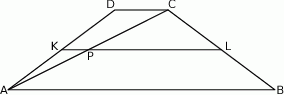
Czworokąt  jest wpisany w okrąg oraz
jest wpisany w okrąg oraz 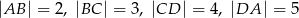 .
.
- Oblicz
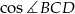 .
. - Oblicz pole czworokąta
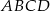 .
.
Na okręgu o promieniu  opisano trapez, w którym
opisano trapez, w którym 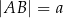 i
i 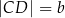 .
.
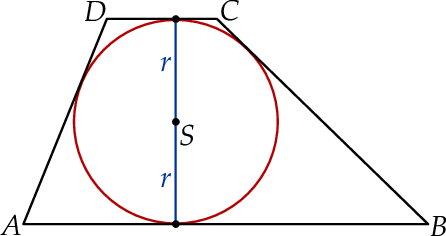
Wykaż, że 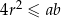 .
.
W trapezie 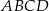 połączono środek
połączono środek 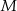 ramienia trapezu
ramienia trapezu 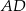 z końcami drugiego ramienia
z końcami drugiego ramienia 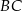 . Wykaż, że pole powstałego trójkąta
. Wykaż, że pole powstałego trójkąta 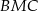 jest równe połowie pola trapezu
jest równe połowie pola trapezu 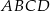 .
.
Punkt 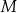 jest środkiem boku
jest środkiem boku 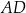 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 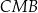 jest połową pola trapezu
jest połową pola trapezu 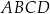 (
(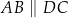 ).
).

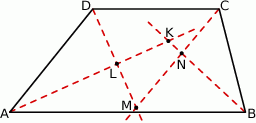
Przekątne czworokąta wypukłego 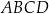 wpisanego w okrąg przecinają się w punkcie
wpisanego w okrąg przecinają się w punkcie 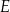 tak, że
tak, że 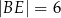 ,
, 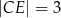 i
i 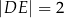 . Ponadto
. Ponadto 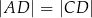 (zobacz rysunek).
(zobacz rysunek).

Oblicz długości boków czworokąta 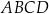 oraz promień opisanego na nim okręgu.
oraz promień opisanego na nim okręgu.
W trapez równoramienny o obwodzie 20 i przekątnej długości 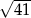 można wpisać okrąg. Oblicz odległości punktu przecięcia przekątnych tego trapezu od prostych zawierających jego boki.
można wpisać okrąg. Oblicz odległości punktu przecięcia przekątnych tego trapezu od prostych zawierających jego boki.
Bok rombu 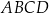 ma długość
ma długość  , a kąt ostry przy wierzchołku
, a kąt ostry przy wierzchołku 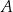 ma miarę
ma miarę 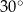 . Oblicz długość odcinka łączącego wierzchołek
. Oblicz długość odcinka łączącego wierzchołek 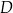 rombu z punktem boku
rombu z punktem boku 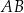 , dzielącego ten bok w stosunku
, dzielącego ten bok w stosunku 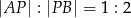 .
.
W czworokącie wypukłym 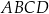 , długości boków
, długości boków 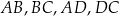 są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że dwusieczne kątów wewnętrznych tego czworokąta przecinają się w jednym punkcie.
są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że dwusieczne kątów wewnętrznych tego czworokąta przecinają się w jednym punkcie.
Różnica między polem koła opisanego na kwadracie a polem koła wpisanego w kwadrat jest równa 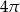 . Oblicz pole kwadratu.
. Oblicz pole kwadratu.
Oblicz pole kwadratu wiedząc, że różnica pól kół opisanego i wpisanego w ten kwadrat jest równa 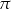 .
.
W trapezie równoramiennym 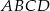 , wysokość
, wysokość 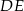 ma długość 6 cm. Punkt
ma długość 6 cm. Punkt 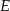 dzieli dłuższą podstawę
dzieli dłuższą podstawę 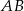 na dwa odcinki. Wiedząc, że
na dwa odcinki. Wiedząc, że 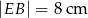 , oblicz pole trapezu
, oblicz pole trapezu 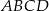 .
.
Dwusieczne kątów wewnętrznych trapezu 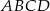 przecinają się w punktach
przecinają się w punktach 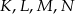 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 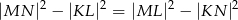 .
.