Punkt 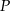 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 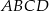 . Wykaż, że wyrażenie
. Wykaż, że wyrażenie 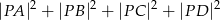 ma stałą wartość, niezależną od wyboru punktu
ma stałą wartość, niezależną od wyboru punktu 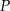 .
.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Dany jest prostokąt 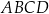 , w którym
, w którym 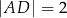 . Kąt
. Kąt 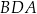 ma miarę
ma miarę  , taką, że
, taką, że 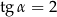 . Przekątna
. Przekątna 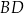 i prosta przechodząca przez wierzchołek
i prosta przechodząca przez wierzchołek 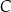 prostopadła do
prostopadła do 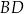 przecinają się w punkcie
przecinają się w punkcie 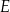 (zobacz rysunek).
(zobacz rysunek).
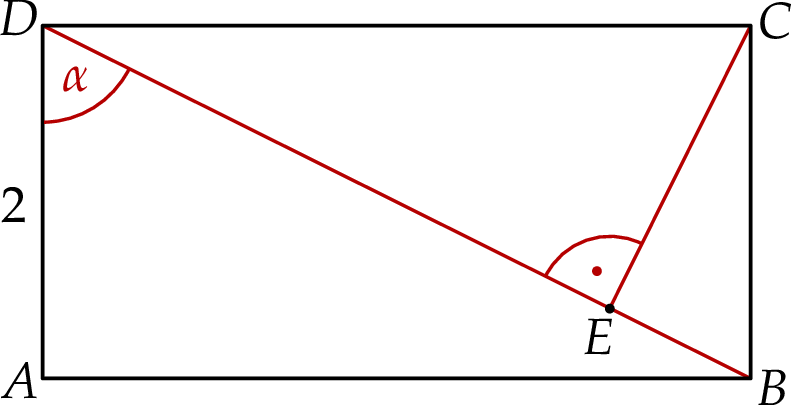
Oblicz długość odcinka 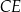 .
.
W trapezie 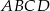 o podstawach
o podstawach 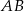 i
i 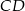 punkt
punkt 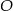 jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta
jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta 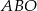 jest równe 5, a pole trójkąta
jest równe 5, a pole trójkąta 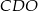 jest równe 4.
jest równe 4.
W trapezie 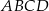 ramię
ramię 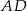 i podstawa
i podstawa 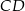 mają długość 4, a ramię
mają długość 4, a ramię 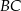 i przekątna
i przekątna 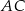 mają długość 6. Oblicz długość podstawy
mają długość 6. Oblicz długość podstawy 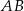 .
.
W równoległoboku 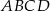 kąt ostry
kąt ostry 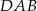 ma miarę
ma miarę 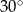 , zaś dłuższy bok ma długość 8. Promień okręgu opisanego na trójkącie
, zaś dłuższy bok ma długość 8. Promień okręgu opisanego na trójkącie 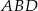 ma długość 4. Oblicz pole równoległoboku.
ma długość 4. Oblicz pole równoległoboku.
Z przeciwległych wierzchołków prostokąta poprowadzono odcinki prostopadłe do przekątnej. Odcinki te dzielą przekątną na trzy części. Każda z nich jest odcinkiem o długości 4 cm. Oblicz pole tego prostokąta.
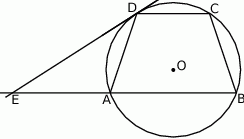
W okrąg wpisano trapez równoramienny 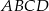 , którego podstawy mają długości:
, którego podstawy mają długości: 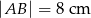 ,
, 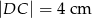 . Styczna do okręgu w punkcie
. Styczna do okręgu w punkcie 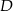 przecina prostą
przecina prostą 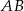 w punkcie
w punkcie 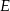 (rys). Wiedząc, że
(rys). Wiedząc, że 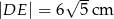 oblicz promień okręgu opisanego na trapezie
oblicz promień okręgu opisanego na trapezie 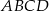 .
.
Podstawy trapezu równoramiennego mają długości  i
i 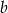 , a jego przekątna ma długość
, a jego przekątna ma długość 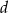 . Wyznacz cosinus kąta między przekątnymi tego trapezu.
. Wyznacz cosinus kąta między przekątnymi tego trapezu.
Podstawy trapezu prostokątnego 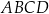 mają długości:
mają długości: 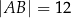 oraz
oraz 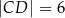 . Wysokość
. Wysokość 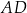 tego trapezu ma długość 24. Na odcinku
tego trapezu ma długość 24. Na odcinku 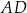 leży punkt
leży punkt 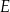 taki, że
taki, że 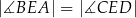 (zobacz rysunek).
(zobacz rysunek).
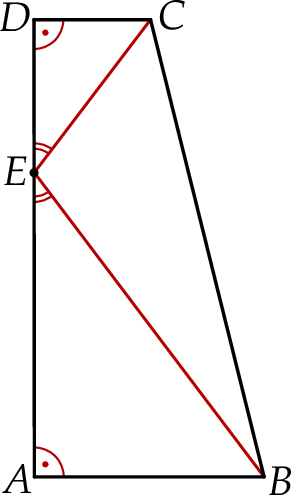
Oblicz długość odcinka 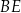 .
.
Dany jest trapez 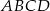 o podstawach
o podstawach 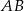 i
i 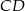 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 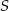 . Wykaż, że
. Wykaż, że 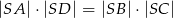 .
.
W trapezie 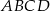 o podstawach
o podstawach 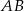 i
i 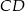 punkt
punkt 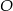 jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta
jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta 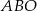 jest równe
jest równe 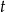 , a pole trójkąta
, a pole trójkąta 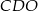 jest równe
jest równe  .
.
Dany jest prostokąt 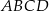 , w którym
, w którym 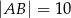 ,
, 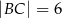 . Odcinek
. Odcinek 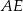 jest wysokością trójkąta
jest wysokością trójkąta 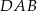 opuszczoną na jego bok
opuszczoną na jego bok 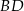 . Oblicz pole trójkąta
. Oblicz pole trójkąta 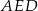 .
.
W okrąg o średnicy 26 wpisano trapez równoramienny w ten sposób, że suma kwadratów długości jego podstaw jest równa 914, a sinus kąta ostrego wynosi 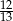 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Punkt 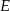 jest punktem wspólnym dwusiecznych kątów
jest punktem wspólnym dwusiecznych kątów 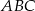 i
i 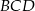 trapezu
trapezu 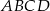 o podstawach
o podstawach 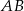 i
i 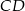 . Punkt
. Punkt 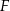 jest środkiem odcinka
jest środkiem odcinka 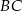 (zobacz rysunek).
(zobacz rysunek).
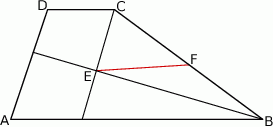
Wykaż, że 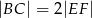 .
.
Na bokach 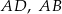 i
i 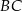 kwadratu
kwadratu 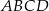 wybrano punkty
wybrano punkty 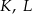 i
i 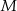 w ten sposób, że
w ten sposób, że 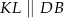 i
i 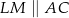 . Uzasadnij, że
. Uzasadnij, że 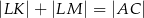 .
.
Na okręgu o promieniu 8 cm opisano trapez. Kąty, które tworzą ramiona z dłuższą podstawą mają miarę 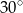 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
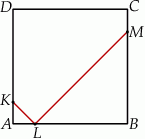
W trapezie prostokątnym 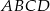 na rysunku poniżej dane są:
na rysunku poniżej dane są: 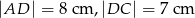 oraz
oraz 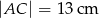 .
.
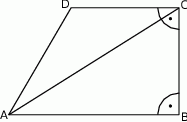
Oblicz:
- miarę kąta ostrego trapezu przy wierzchołku
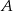 ,
, - długość odcinka łączącego środki ramion tego trapezu.
Prosta przechodząca przez środek 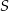 kwadratu
kwadratu 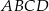 przecina proste zawierające jego boki
przecina proste zawierające jego boki 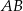 i
i 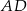 odpowiednio w punktach
odpowiednio w punktach 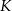 i
i 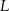 (zobacz rysunek).
(zobacz rysunek).
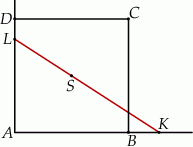
Wykaż, że
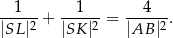
Na rysunku przedstawiono trapez 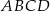 i trójkąt
i trójkąt 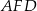 . Punkt
. Punkt 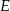 leży w połowie odcinka
leży w połowie odcinka 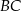 . Uzasadnij, że pole trapezu
. Uzasadnij, że pole trapezu 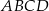 i pole trójkąta
i pole trójkąta 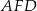 są równe.
są równe.
Oblicz pole trapezu, którego podstawy mają długości 2 i 3, a przekątne długości 3 i 4.

