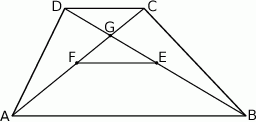
W trapezie 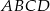 o podstawach
o podstawach 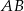 i
i 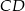 dane są długości przekątnych
dane są długości przekątnych 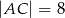 i
i 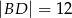 oraz pola
oraz pola 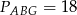 i
i 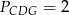 . Punkty
. Punkty  i
i 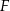 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 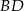 i
i 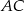 .
.
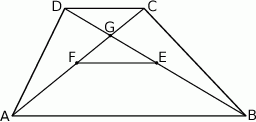
Oblicz pole trapezu 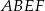 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trapezie 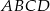 o podstawach
o podstawach 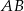 i
i 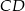 dane są długości przekątnych
dane są długości przekątnych 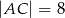 i
i 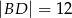 oraz pola
oraz pola 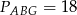 i
i 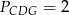 . Punkty
. Punkty 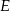 i
i 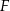 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 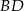 i
i 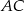 .
.

Oblicz pole trapezu 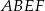 .
.
W trapezie 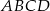 o podstawach
o podstawach 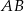 i
i 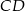 dane są długości przekątnych
dane są długości przekątnych 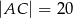 i
i 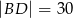 oraz pola
oraz pola 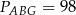 i
i 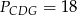 . Punkty
. Punkty 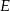 i
i 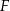 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 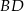 i
i 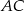 .
.
Oblicz pole trójkąta 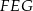 .
.
Pole trapezu jest równe  , a stosunek długości jego podstaw wynosi
, a stosunek długości jego podstaw wynosi  . Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
. Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
Na czworokącie wypukłym 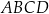 można opisać okrąg. Wiadomo, że
można opisać okrąg. Wiadomo, że 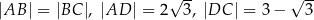 oraz przekątna
oraz przekątna 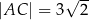 . Oblicz pole tego czworokąta.
. Oblicz pole tego czworokąta.
W trapezie 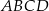 mamy
mamy 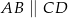 oraz
oraz 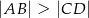 . Punkt
. Punkt 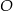 jest środkiem ramienia
jest środkiem ramienia 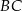 , a punkt
, a punkt 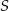 jest punktem wspólnym prostych
jest punktem wspólnym prostych 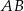
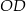 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 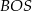 jest równe polu trójkąta
jest równe polu trójkąta 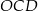 .
.
Obwód prostokąta wynosi 60 cm. Jeśli krótszy bok tego prostokąta zwiększymy o 3 cm, a dłuższy skrócimy o 3 cm, to otrzymamy kwadrat. Wyznacz kąt pomiędzy przekątną, a dłuższym bokiem prostokąta. Wynik podaj z dokładnością do 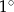 .
.
Obwód prostokąta wynosi 32 cm. Jeśli krótszy bok tego prostokąta zwiększymy o 3 cm, a dłuższy skrócimy o 3 cm, to otrzymamy kwadrat. Wyznacz kąt pomiędzy przekątną, a dłuższym bokiem prostokąta. Wynik podaj z dokładnością do 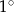 .
.
Bok kwadratu 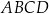 ma długość równą 12. Punkt
ma długość równą 12. Punkt 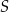 jest środkiem boku
jest środkiem boku 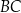 tego kwadratu. Na odcinku
tego kwadratu. Na odcinku 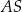 leży punkt
leży punkt 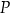 taki, że odcinek
taki, że odcinek 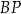 jest prostopadły do odcinka
jest prostopadły do odcinka 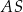 . Oblicz długość odcinka
. Oblicz długość odcinka 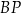 .
.
Dany jest trapez równoramienny 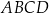 , w którym podstawa
, w którym podstawa 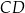 ma długość 6, ramię
ma długość 6, ramię 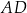 ma długość 4, a kąty
ma długość 4, a kąty 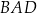 oraz
oraz 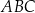 mają miarę
mają miarę 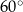 (zobacz rysunek).
(zobacz rysunek).
Oblicz pole tego trapezu.
Dany jest trapez równoramienny  , w którym podstawa
, w którym podstawa  ma długość 8, ramię
ma długość 8, ramię 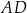 ma długość 6, a kąty
ma długość 6, a kąty 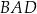 oraz
oraz 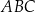 mają miarę
mają miarę 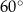 (zobacz rysunek).
(zobacz rysunek).
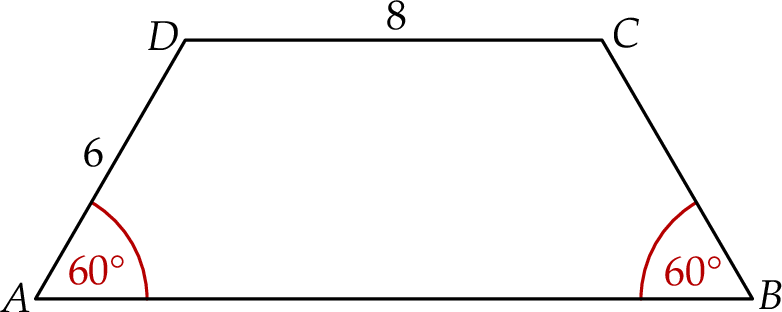
Oblicz pole tego trapezu.
W okrąg o promieniu 7 wpisano czworokąt  . Oblicz obwód i pole tego czworokąta, wiedząc, że
. Oblicz obwód i pole tego czworokąta, wiedząc, że  ,
,  i stosunek pola trójkąta
i stosunek pola trójkąta 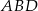 do pola trójkąta
do pola trójkąta 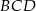 wynosi 2:1.
wynosi 2:1.
Trapez 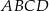 jest wpisany w okrąg, przekątna
jest wpisany w okrąg, przekątna 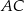 jest zawarta w dwusiecznej kąta
jest zawarta w dwusiecznej kąta 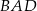 , a długość podstawy
, a długość podstawy 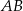 jest dwa razy większa niż długość podstawy
jest dwa razy większa niż długość podstawy 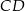 . Oblicz pole trapezu i obwód wiedząc że jego wysokość jest równa
. Oblicz pole trapezu i obwód wiedząc że jego wysokość jest równa 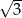 .
.
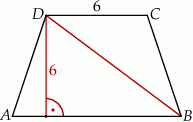
Dany jest trapez 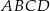 o podstawach
o podstawach 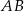 i
i 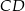 , w którym
, w którym 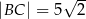 . Okrąg opisany na trójkącie
. Okrąg opisany na trójkącie 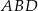 przecina prostą
przecina prostą 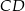 w takim punkcie
w takim punkcie 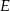 , że
, że 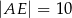 i
i 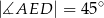 . Oblicz długość podstawy
. Oblicz długość podstawy 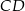 trapezu
trapezu 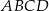 .
.
Wykaż, że w trapezie prostokątnym różnica kwadratów długości przekątnych równa jest różnicy kwadratów długości podstaw.
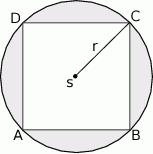
Na kwadracie 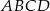 opisano okrąg o promieniu
opisano okrąg o promieniu 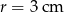 . Oblicz pole zacieniowanej figury.
. Oblicz pole zacieniowanej figury.
Na kwadracie  opisano okrąg o promieniu
opisano okrąg o promieniu 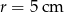 . Oblicz pole zacieniowanej figury.
. Oblicz pole zacieniowanej figury.
W trapezie równoramiennym 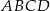 krótsza podstawa
krótsza podstawa 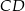 ma długość równą 6 i jest równa wysokości trapezu. Długość dłuższej podstawy
ma długość równą 6 i jest równa wysokości trapezu. Długość dłuższej podstawy 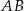 jest równa długości przekątnej trapezu. Oblicz pole tego trapezu.
jest równa długości przekątnej trapezu. Oblicz pole tego trapezu.
Dany jest prostokąt  , w którym
, w którym  . Na przekątnej
. Na przekątnej  leży punkt
leży punkt 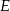 taki, że
taki, że 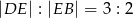 oraz
oraz 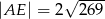 . Oblicz pole prostokąta
. Oblicz pole prostokąta 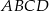 .
.
Podstawy trapezu prostokątnego mają długości 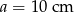 i
i 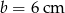 , zaś bok prostopadły do podstaw ma długość
, zaś bok prostopadły do podstaw ma długość 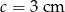 .
.
 i ramienia długości
i ramienia długości  .
. Trapez równoramienny jest opisany na okręgu. Obwód trapezu wynosi 16cm, a przekątna ma długość 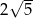 . Oblicz długości boków tego trapezu.
. Oblicz długości boków tego trapezu.
Oblicz pole trapezu 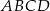 , którego podstawy mają długości
, którego podstawy mają długości 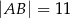 i
i 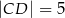 , a ramiona mają długości
, a ramiona mają długości 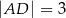 i
i 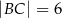 .
.
W trapezie równoramiennym o podstawach długości 20 i 40, oraz kącie ostrym o mierze 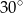 połączono środki wszystkich boków. Oblicz pole otrzymanego czworokąta.
połączono środki wszystkich boków. Oblicz pole otrzymanego czworokąta.
W trapezie 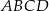 dane są długości podstaw:
dane są długości podstaw: 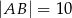 ,
, 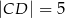 i ramion:
i ramion: 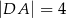 ,
, 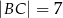 . Oblicz długość przekątnej
. Oblicz długość przekątnej 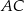 tego trapezu.
tego trapezu.
Obwód rombu wynosi 68 cm, a długość jednej z jego przekątnych stanowi 187,5% długości drugiej przekątnej. Oblicz pole tego rombu.
