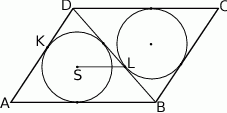
Dany jest równoległobok 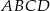 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 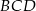 jest styczny do przekątnej
jest styczny do przekątnej 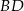 w punkcie
w punkcie 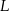 , a okrąg wpisany w trójkąt
, a okrąg wpisany w trójkąt 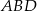 ma środek
ma środek 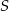 i jest styczny do boku
i jest styczny do boku 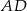 w punkcie
w punkcie 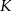 .
.
Wykaż, że jeżeli odcinek 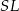 jest równoległy do prostej
jest równoległy do prostej 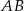 , to
, to 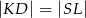 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest równoległobok 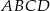 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 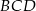 jest styczny do przekątnej
jest styczny do przekątnej 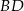 w punkcie
w punkcie 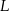 , a okrąg wpisany w trójkąt
, a okrąg wpisany w trójkąt 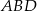 ma środek
ma środek 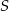 i jest styczny do boku
i jest styczny do boku 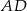 w punkcie
w punkcie 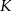 .
.

Wykaż, że jeżeli odcinek 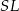 jest równoległy do prostej
jest równoległy do prostej 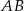 , to
, to 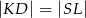 .
.
Przekątne równoległoboku 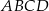 mają długości:
mają długości: 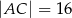 oraz
oraz 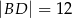 . Wierzchołki
. Wierzchołki 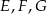 oraz
oraz  rombu
rombu  leżą na bokach równoległoboku
leżą na bokach równoległoboku  (zobacz rysunek). Boki tego rombu są równoległe do przekątnych równoległoboku.
(zobacz rysunek). Boki tego rombu są równoległe do przekątnych równoległoboku.
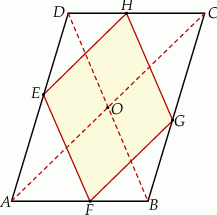
Oblicz długość boku rombu  .
.
Trapez równoramienny o podstawach długości  i
i 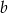 opisany jest na okręgu. Oblicz pole koła, którego brzegiem jest okrąg wpisany w ten trapez.
opisany jest na okręgu. Oblicz pole koła, którego brzegiem jest okrąg wpisany w ten trapez.
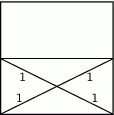
W kwadracie połączono odcinkiem środki przeciwległych boków. Wiedząc, że przekątne tak utworzonych prostokątów dzielą się na odcinki długości 1, oblicz pole wyjściowego kwadratu.
Proste zawierające ramiona 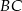 i
i 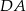 trapezu
trapezu  przecinają się w punkcie
przecinają się w punkcie  . Dane są:
. Dane są: 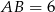 ,
, 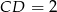 oraz obwód trójkąta
oraz obwód trójkąta 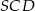 równy
równy 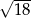 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta  .
.
Oblicz wysokość i przekątną trapezu równoramiennego o podstawach 21 cm i 11 cm oraz ramieniu równym 13 cm.
Bok rombu ma długość 13, suma długości przekątnych jest równa 34.
W prostokącie, którego krótszy bok ma długość 8 zawarty jest kwadrat o boku równym różnicy
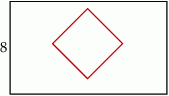
długości boków prostokąta, i którego przekątne są równoległe do boków prostokąta.
Przekątne trapezu przecinają się w punkcie 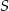 . Przez punkt
. Przez punkt 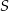 poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach
poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach 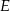 i
i 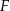 . Wykaż, że
. Wykaż, że 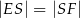 .
.
W trapezie 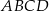 o podstawach
o podstawach 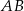 i
i 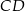 przez punkt
przez punkt  przecięcia się przekątnych poprowadzono dwie proste równoległe do boków
przecięcia się przekątnych poprowadzono dwie proste równoległe do boków 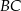 i
i 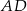 . Prosta równoległa do boku
. Prosta równoległa do boku 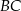 przecina bok
przecina bok 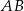 w punkcie
w punkcie 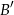 , a prosta równoległa do boku
, a prosta równoległa do boku 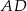 przecina bok
przecina bok 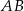 w punkcie
w punkcie 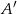 . Wykaż, że
. Wykaż, że 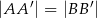 .
.
W kwadrat 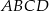 o boku długości
o boku długości 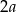 wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek
wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek 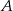 ze środkiem boku
ze środkiem boku 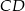 .
.
W trójkąt równoramienny, którego ramię jest równe 5 cm, a podstawa równa się 6 cm, wpisano prostokąt w ten sposób, że dwa jego wierzchołki leżą na podstawie, a pozostałe leżą na ramionach trójkąta. Wyznacz obwód i pole prostokąta jako funkcję jego wysokości.
W trapezie równoramiennym 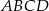 ramię ma długość 10. Obwód tego trapezu jest równy 40. Wiedząc, że tangens kąta ostrego w trapezie
ramię ma długość 10. Obwód tego trapezu jest równy 40. Wiedząc, że tangens kąta ostrego w trapezie 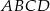 jest równy
jest równy  , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
W trapezie równoramiennym 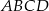 ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie
ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie 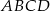 jest równy
jest równy 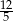 , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
Punkt styczności okręgu o promieniu  wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 1:2. Oblicz promień okręgu opisanego na tym trapezie.
wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 1:2. Oblicz promień okręgu opisanego na tym trapezie.
Punkt styczności okręgu o promieniu  wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 2:5. Oblicz promień okręgu opisanego na tym trapezie.
wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 2:5. Oblicz promień okręgu opisanego na tym trapezie.
Dany jest kwadrat 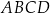 o boku długości 2. Punkt
o boku długości 2. Punkt 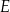 jest punktem przekątnej
jest punktem przekątnej 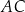 , takim że
, takim że 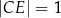 . Oblicz długość odcinka
. Oblicz długość odcinka 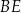 .
.
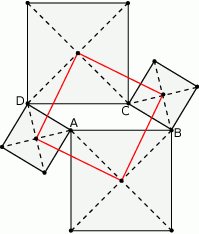
Wykazać, że odcinki łączące kolejne środki kwadratów zbudowanych na bokach równoległoboku tworzą także kwadrat.
Długość boku rombu jest równa  , a długości jego przekątnych są równe
, a długości jego przekątnych są równe 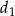 i
i 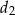 . Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że
. Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że 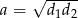 .
.
Długość boku rombu 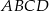 jest średnią geometryczną długości jego przekątnych. Oblicz miarę kąta ostrego tego rombu.
jest średnią geometryczną długości jego przekątnych. Oblicz miarę kąta ostrego tego rombu.
Z dwóch przeciwległych wierzchołków kwadratu o boku 2 zakreślono okręgi o promieniu 2. Oblicz pole „soczewki” wyznaczonej przez te okręgi.
Środek okręgu wpisanego w trapez prostokątny, znajduje się w odległości 4 oraz 8 od końców dłuższego ramienia trapezu. Oblicz pole tego trapezu.
Środek okręgu wpisanego w trapez prostokątny znajduje się w odległości 2 cm i 4 cm od końców ramienia pochyłego danego trapezu. Znaleźć pole trapezu.
Krótsza przekątna równoległoboku tworzy bokami kąty  i
i 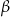 . Oblicz stosunek długości boków tego równoległoboku.
. Oblicz stosunek długości boków tego równoległoboku.
W równoległoboku, który nie jest prostokątem, krótsza przekątna dzieli go na dwa równoramienne trójkąty prostokątne. Krótszy bok równoległoboku ma długość 8. Oblicz pole tego równoległoboku.
