Dla dowolnej liczby 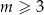 , prosta
, prosta 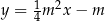 przecina hiperbolę
przecina hiperbolę 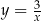 w punktach
w punktach 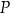 i
i 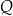 . Uzasadnij, że
. Uzasadnij, że 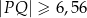 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum/Najmniejsza długość
Na prostej o równaniu 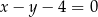 znajdź punkt
znajdź punkt 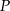 , którego kwadrat odległości od punktu
, którego kwadrat odległości od punktu 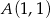 jest najmniejszy.
jest najmniejszy.
Na prostej o równaniu 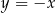 wyznacz współrzędne punktu
wyznacz współrzędne punktu  leżącego najbliżej punktu
leżącego najbliżej punktu 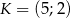 .
.
Na prostej o równaniu 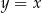 wyznacz współrzędne punktu
wyznacz współrzędne punktu 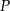 leżącego najbliżej punktu
leżącego najbliżej punktu 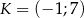 .
.
Dany jest ciąg punktów 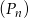 na płaszczyźnie, których współrzędne dane są wzorem
na płaszczyźnie, których współrzędne dane są wzorem 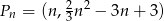 , gdzie
, gdzie 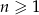 . Wyznacz tę wartość
. Wyznacz tę wartość  , dla której odległość punktu
, dla której odległość punktu 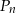 od prostej
od prostej 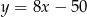 jest najmniejsza z możliwych.
jest najmniejsza z możliwych.
Dane są punkty 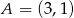 i
i 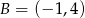 oraz prosta
oraz prosta 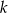 o równaniu
o równaniu 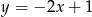 . Wyznacz taki punkt
. Wyznacz taki punkt 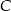 prostej
prostej 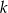 , aby suma kwadratów boków trójkąta
, aby suma kwadratów boków trójkąta 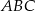 była najmniejsza możliwa. Oblicz tę najmniejszą sumę kwadratów długości boków.
była najmniejsza możliwa. Oblicz tę najmniejszą sumę kwadratów długości boków.
Który z odcinków łączących dowolny punkt paraboli o równaniu 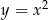 z punktem
z punktem 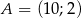 ma najmniejszy kwadrat długości?
ma najmniejszy kwadrat długości?
Wyznacz te punkty paraboli 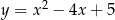 , które znajdują się najbliżej punktu
, które znajdują się najbliżej punktu 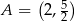 . Oblicz tę najmniejszą odległość.
. Oblicz tę najmniejszą odległość.
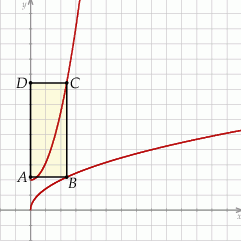
Rozpatrujemy prostokąty 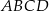 , których dwa wierzchołki leżą na osi
, których dwa wierzchołki leżą na osi 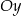 , jeden wierzchołek leży na paraboli określonej równaniem
, jeden wierzchołek leży na paraboli określonej równaniem 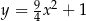 , jeden wierzchołek leży na wykresie funkcji
, jeden wierzchołek leży na wykresie funkcji 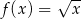 określonej dla
określonej dla 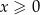 . Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.
. Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.
Na paraboli o równaniu 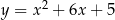 znajdź współrzędne punktu
znajdź współrzędne punktu 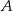 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 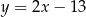 jest najmniejsza.
jest najmniejsza.
Na paraboli o równaniu 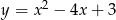 wyznacz punkt, którego odległość od prostej
wyznacz punkt, którego odległość od prostej 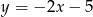 jest najmniejsza.
jest najmniejsza.
Wyznacz wartość parametru 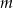 , dla której odległość punktu
, dla której odległość punktu 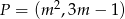 od prostej
od prostej 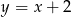 jest najmniejsza możliwa.
jest najmniejsza możliwa.
Na wykresie funkcji 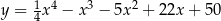 znajdź współrzędne punktu
znajdź współrzędne punktu 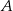 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 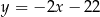 jest najmniejsza.
jest najmniejsza.
Na wykresie funkcji 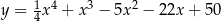 znajdź współrzędne punktu
znajdź współrzędne punktu 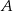 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 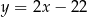 jest najmniejsza.
jest najmniejsza.
W parku krajobrazowym znajduje się zbiornik wodny, którego dwa brzegi postanowiono połączyć pomostem. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej zbiornika w kartezjańskim układzie współrzędnych  za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 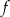 oraz
oraz 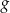 , które odpowiadają przeciwległym brzegom zbiornika (zobacz rysunek).
, które odpowiadają przeciwległym brzegom zbiornika (zobacz rysunek).
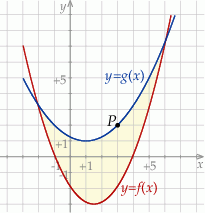
Funkcje 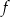 oraz
oraz 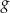 są określone wzorami
są określone wzorami 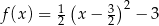 oraz
oraz 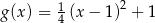 . Jeden z końców pomostu postanowiono zlokalizować na brzegu opisanym funkcją
. Jeden z końców pomostu postanowiono zlokalizować na brzegu opisanym funkcją 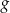 w punkcie o współrzędnych
w punkcie o współrzędnych 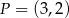 . Koniec pomostu należy umieścić na brzegu opisanym funkcją
. Koniec pomostu należy umieścić na brzegu opisanym funkcją 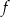 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 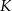 , w którym należy zlokalizować koniec pomostu, aby jego długość (tj. odległość końca
, w którym należy zlokalizować koniec pomostu, aby jego długość (tj. odległość końca 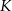 pomostu od początku
pomostu od początku 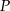 ) była możliwie najmniejsza. Oblicz długość najkrótszego pomostu.
) była możliwie najmniejsza. Oblicz długość najkrótszego pomostu.
Przy rozwiązywaniu zadania możesz skorzystać z tego, że odległość dowolnego punktu 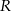 leżącego na wykresie funkcji
leżącego na wykresie funkcji 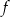 od punktu
od punktu 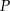 wyraża się wzorem
wyraża się wzorem
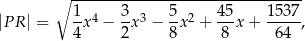
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 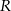 .
.
Dane są punkty 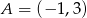 i
i 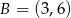 . Funkcja
. Funkcja 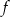 przyporządkowuje dowolnemu punktowi należącemu do odcinka
przyporządkowuje dowolnemu punktowi należącemu do odcinka 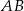 jego odległość od punktu
jego odległość od punktu 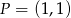 . Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.
. Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.
Na rysunku przedstawiono położenie miejscowości  i
i 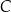 oraz zaznaczono odległości między nimi. O godzinie 9:00 z miejscowości
oraz zaznaczono odległości między nimi. O godzinie 9:00 z miejscowości 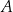 do
do 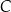 wyruszył zastęp harcerzy Tropiciele i przemieszczał się z prędkością 4 km/h. O tej samej godzinie z miejscowości
wyruszył zastęp harcerzy Tropiciele i przemieszczał się z prędkością 4 km/h. O tej samej godzinie z miejscowości 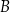 do
do  wyruszył zastęp harcerzy Korsarze i przemieszczał się z prędkością 2 km/h.
wyruszył zastęp harcerzy Korsarze i przemieszczał się z prędkością 2 km/h.
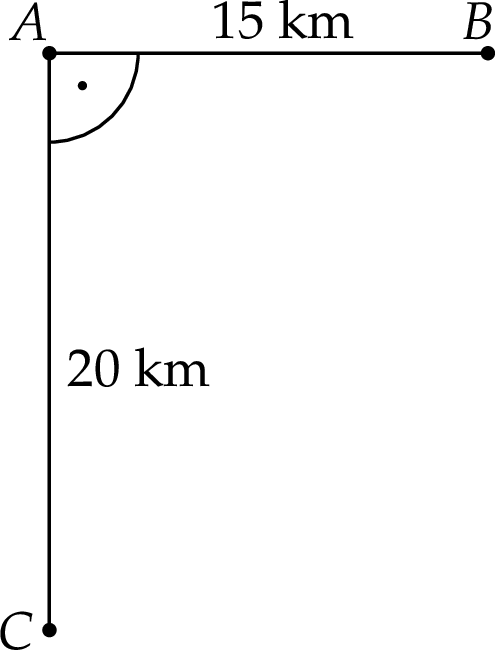
Wyznacz godzinę, o której odległość między tymi zastępami harcerzy będzie najmniejsza. Przyjmij, że mierzymy odległość między zastępami do momentu, w którym zastęp Tropicieli dotrze do miejscowości  .
.

