Znajdź wielomian o współczynnikach całkowitych, którego pierwiastkiem jest liczba 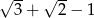 .
.
/Konkursy/Zadania/Równania
Wykaż, że jeżeli liczby rzeczywiste 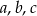 spełniają równość
spełniają równość 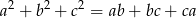 to
to 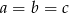 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  ,
, 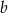 i
i  , funkcja
, funkcja
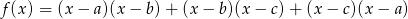
ma co najmniej jedno miejsce zerowe.
Wykaż, że wielomian 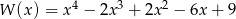 nie ma pierwiastków rzeczywistych.
nie ma pierwiastków rzeczywistych.
Uzasadnij, że równanie 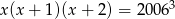 nie ma pierwiastków całkowitych.
nie ma pierwiastków całkowitych.
Rozwiąż układ równań 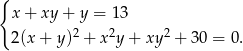
Wyznacz wszystkie liczby naturalne dodatnie 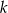 , dla których równanie
, dla których równanie 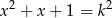 ma pierwiastki będące liczbami całkowitymi.
ma pierwiastki będące liczbami całkowitymi.
Wyznacz wszystkie pary liczb całkowitych 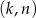 spełniających równość
spełniających równość 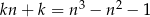 .
.
Wyznacz wszystkie pary 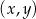 , gdzie
, gdzie  i
i 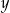 są liczbami całkowitymi spełniającymi równanie
są liczbami całkowitymi spełniającymi równanie
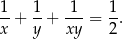
Liczby naturalne  i
i 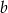 spełniają równość
spełniają równość 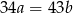 . Udowodnij, że liczba
. Udowodnij, że liczba 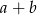 jest złożona.
jest złożona.
Wyznacz wszystkie liczby całkowite 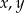 spełniające równanie
spełniające równanie 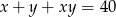 .
.
Liczby 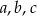 są rozwiązaniami równania
są rozwiązaniami równania 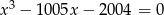 . Napisz równanie którego rozwiązaniami są liczby
. Napisz równanie którego rozwiązaniami są liczby 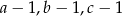 .
.
Wykaż, że nie istnieje para liczb 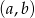 spełniająca układ równań
spełniająca układ równań 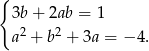
Wykaż, że jeżeli między współczynnikami trójmianów 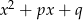 i
i 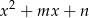 zachodzi związek
zachodzi związek 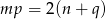 , to przynajmniej jedno z równań
, to przynajmniej jedno z równań 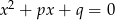 lub
lub 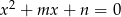 ma rozwiązanie.
ma rozwiązanie.
Wielomian 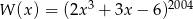 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 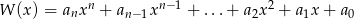 . Oblicz sumę
. Oblicz sumę 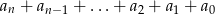 .
.
Wykaż, że jeżeli wielomian 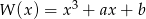 ma pierwiastek dwukrotny, to
ma pierwiastek dwukrotny, to 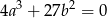 .
.
Ile jest takich czwórek liczb całkowitych i dodatnich 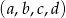 , które spełniają równanie
, które spełniają równanie 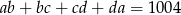 .
.
Uzasadnij, że równanie 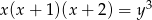 nie ma rozwiązań w liczbach całkowitych dodatnich
nie ma rozwiązań w liczbach całkowitych dodatnich 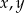 .
.
Wykaż, że jeżeli liczby całkowite  i
i 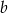 spełniają równanie
spełniają równanie
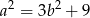
to liczba 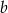 dzieli się przez 3, a liczba
dzieli się przez 3, a liczba  nie dzieli się przez 9.
nie dzieli się przez 9.
Udowodnij, że jeżeli 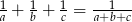 to
to 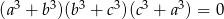 .
.

