Wielomian 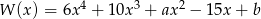 jest podzielny przez trójmian
jest podzielny przez trójmian 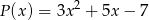 . Wyznacz liczby
. Wyznacz liczby  i
i 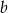 .
.
/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 2
Nie wykonując dzielenia, wyznacz resztę z dzielenia wielomianu 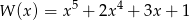 przez
przez 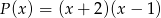 .
.
Wielomian 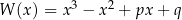 można dwukrotnie podzielić bez reszty przez dwumian
można dwukrotnie podzielić bez reszty przez dwumian 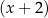 . Oblicz
. Oblicz 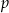 i
i 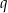 .
.
Reszta z dzielenia wielomianu 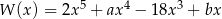 przez trójmian
przez trójmian 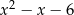 jest równa
jest równa 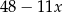 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 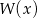 przez trójmian
przez trójmian 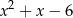 .
.
W wyniku dzielenia wielomianu 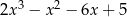 przez dwumian
przez dwumian 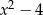 otrzymujemy resztę postaci
otrzymujemy resztę postaci 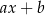 . Oblicz
. Oblicz  i
i 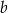 .
.
Reszta z dzielenia wielomianu 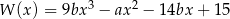 przez trójmian
przez trójmian 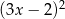 wynosi 3. Oblicz
wynosi 3. Oblicz  i
i 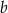 . Dla wyznaczonych wartości
. Dla wyznaczonych wartości  i
i 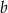 rozwiąż nierówność
rozwiąż nierówność 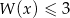 .
.
Wielomian 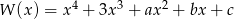 jest podzielny przez trójmian
jest podzielny przez trójmian 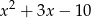 , a przy dzieleniu przez dwumian
, a przy dzieleniu przez dwumian 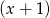 daje resztę -36. Wyznacz współczynniki
daje resztę -36. Wyznacz współczynniki 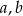 i
i  wielomianu.
wielomianu.
Dany jest wielomian 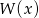 stopnia
stopnia 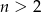 , którego suma wszystkich współczynników jest równa 4, a suma współczynników przy potęgach o wykładnikach nieparzystych jest równa sumie współczynników przy potęgach o wykładnikach parzystych. Wykaż, że reszta
, którego suma wszystkich współczynników jest równa 4, a suma współczynników przy potęgach o wykładnikach nieparzystych jest równa sumie współczynników przy potęgach o wykładnikach parzystych. Wykaż, że reszta 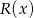 z dzielenia tego wielomianu przez wielomian
z dzielenia tego wielomianu przez wielomian 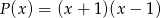 jest równa
jest równa 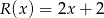 .
.
Reszta z dzielenia wielomianu 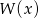 przez wielomian
przez wielomian 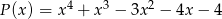 jest wielomianem
jest wielomianem 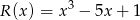 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 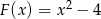 .
.
Reszta z dzielenia wielomianu 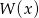 przez wielomian
przez wielomian 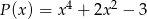 jest wielomianem
jest wielomianem 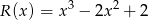 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 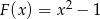 .
.
Wielomian 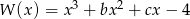 jest podzielny przez trójmian kwadratowy
jest podzielny przez trójmian kwadratowy 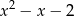 . Wyznacz współczynniki
. Wyznacz współczynniki 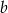 i
i  wielomianu
wielomianu 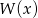 .
.
Wielomian 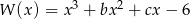 jest podzielny przez trójmian kwadratowy
jest podzielny przez trójmian kwadratowy 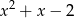 . Wyznacz współczynniki
. Wyznacz współczynniki 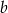 i
i  wielomianu
wielomianu 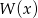 .
.
Wykaż, że jeżeli wielomian 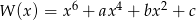 jest podzielny przez trójmian
jest podzielny przez trójmian 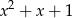 , to jest również podzielny przez trójmian
, to jest również podzielny przez trójmian 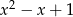 .
.
Wielomian 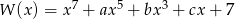 jest podzielny przez wielomian
jest podzielny przez wielomian 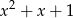 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 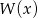 przez wielomian
przez wielomian 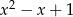 .
.
Wyznacz resztę z dzielenia wielomianu 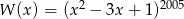 przez wielomian
przez wielomian 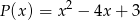 .
.
Reszta z dzielenia wielomianu 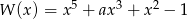 przez dwumian
przez dwumian 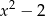 jest równa 1. Oblicz wartość współczynnika
jest równa 1. Oblicz wartość współczynnika  .
.
Reszta z dzielenia wielomianu 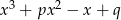 przez trójmian
przez trójmian 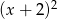 wynosi
wynosi 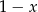 . Wyznacz pierwiastki tego wielomianu.
. Wyznacz pierwiastki tego wielomianu.
Wyznacz resztę z dzielenia wielomianu 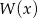 przez wielomian
przez wielomian 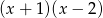 wiedząc, że
wiedząc, że 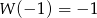 i
i 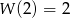 .
.
Wyznacz resztę z dzielenia wielomianu 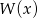 przez wielomian
przez wielomian 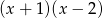 wiedząc, że
wiedząc, że 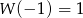 i
i 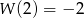 .
.
Wyznacz resztę z dzielenia wielomianu 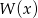 przez wielomian
przez wielomian 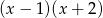 wiedząc, że
wiedząc, że 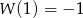 i
i 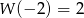 .
.
Reszta z dzielenia wielomianu 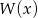 przez wielomian
przez wielomian 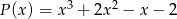 jest równa
jest równa 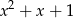 . Wyznacz resztę z dzielenia wielomianu
. Wyznacz resztę z dzielenia wielomianu 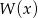 przez wielomian
przez wielomian 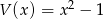 .
.
Liczba -7 jest miejscem zerowym 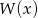 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 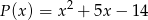 , jeśli wiadomo, że w wyniku dzielenia wielomianu
, jeśli wiadomo, że w wyniku dzielenia wielomianu 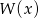 przez dwumian
przez dwumian 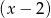 otrzymujemy resztę 18.
otrzymujemy resztę 18.
Wykaż, że wielomian 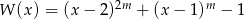 jest podzielny przez wielomian
jest podzielny przez wielomian 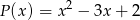 dla każdego
dla każdego 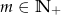 .
.
Liczba 2 jest miejscem zerowym wielomianu 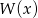 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 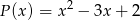 jeśli wiadomo, że w wyniku dzielenia wielomianu
jeśli wiadomo, że w wyniku dzielenia wielomianu 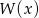 przez dwumian
przez dwumian 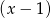 otrzymujemy resztę 5.
otrzymujemy resztę 5.

