Dana jest kula o objętości 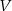 i polu polu powierzchni
i polu polu powierzchni 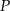 . W tabeli przedstawiono kilka wyrażeń.
. W tabeli przedstawiono kilka wyrażeń.
| Wyrażenie | I | II | III | IV |
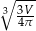 | 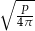 | 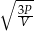 | 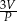 |
Które z tych wyrażeń nie jest równe promieniowi danej kuli?
A) Wyrażenie I B) Wyrażenie II C) Wyrażenie III D) Wyrażenie IV

 , a Paweł poprawnie zaokrąglił liczbę 3495 do pełnych tysięcy i otrzymał liczbę
, a Paweł poprawnie zaokrąglił liczbę 3495 do pełnych tysięcy i otrzymał liczbę 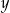 . Czy liczby
. Czy liczby  i
i 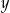 są równe? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.
są równe? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.  , a Ania poprawnie zaokrągliła liczbę 6489 do pełnych tysięcy i otrzymała liczbę
, a Ania poprawnie zaokrągliła liczbę 6489 do pełnych tysięcy i otrzymała liczbę 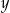 . Czy liczby
. Czy liczby  i
i 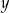 są równe? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.
są równe? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.  i
i 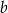 do pełnych dziesiątek są takie same. Czy cyfry tysięcy liczb
do pełnych dziesiątek są takie same. Czy cyfry tysięcy liczb  i
i 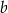 muszą być takie same? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.
muszą być takie same? Wybierz odpowiedź T lub N i jej uzasadnienie spośród A, B albo C.  i
i 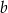 różnią się o co najwyżej 10.
różnią się o co najwyżej 10.  i
i 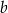 może być liczba podzielna przez 1000.
może być liczba podzielna przez 1000. 
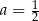 ,
, 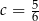 i
i 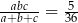 , to
, to 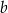 jest równe
jest równe 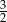
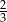
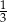

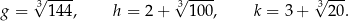
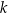 jest większa od liczby
jest większa od liczby 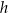 .
. 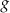 nie jest największą spośród liczb:
nie jest największą spośród liczb: 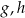 i
i 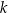 .
.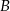 jest środkiem okręgu. Prosta
jest środkiem okręgu. Prosta 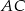 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 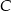 ,
, 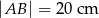 i
i 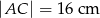 .
. 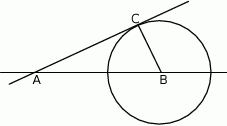
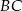 okręgu ma długość
okręgu ma długość 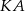 i
i 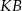 są styczne do okręgu o środku
są styczne do okręgu o środku 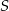 w punktach
w punktach 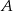 i
i 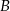 , a kąt
, a kąt 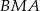 ma miarę
ma miarę 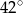 (rysunek).
(rysunek). 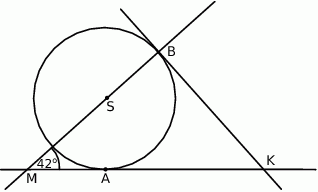
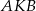 jest równy
jest równy 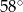
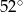
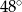
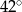
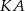 i
i 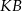 są styczne do okręgu o środku
są styczne do okręgu o środku 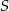 w punktach
w punktach 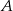 i
i 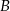 , a kąt
, a kąt 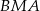 ma miarę
ma miarę 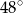 (rysunek).
(rysunek). 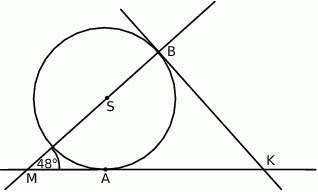
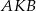 jest równy
jest równy 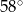
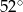
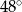
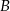 jest środkiem okręgu. Prosta
jest środkiem okręgu. Prosta 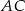 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 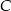 ,
, 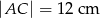 i
i 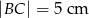 .
. 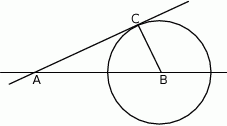
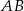 jest równa
jest równa 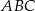 o boku długości 10 cm. W tym trójkącie poprowadzono wysokość
o boku długości 10 cm. W tym trójkącie poprowadzono wysokość 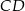 . Obwód trójkąta
. Obwód trójkąta 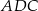 jest równy
jest równy 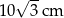
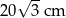
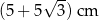
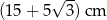
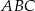 o boku długości 8 cm. W tym trójkącie poprowadzono wysokość
o boku długości 8 cm. W tym trójkącie poprowadzono wysokość 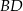 . Obwód trójkąta
. Obwód trójkąta 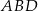 jest równy
jest równy 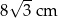
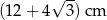
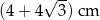
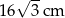
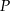 ) wypłynęły jednocześnie na połów dwa kutry: jeden na północ ze stałą prędkością 4 węzłów, drugi na wschód ze stałą prędkością 3 węzłów. Oblicz odległość między tymi kutrami po dwóch godzinach od wypłynięcia. Wynik podaj w kilometrach. Zapisz obliczenia.
) wypłynęły jednocześnie na połów dwa kutry: jeden na północ ze stałą prędkością 4 węzłów, drugi na wschód ze stałą prędkością 3 węzłów. Oblicz odległość między tymi kutrami po dwóch godzinach od wypłynięcia. Wynik podaj w kilometrach. Zapisz obliczenia. 
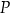 ) wypłynęły jednocześnie na połów dwa kutry: jeden na północ ze stałą prędkością 4 węzłów, drugi na wschód ze stałą prędkością 3 węzłów. Oblicz odległość między tymi kutrami po trzech godzinach od wypłynięcia. Wynik podaj w kilometrach. Zapisz obliczenia.
) wypłynęły jednocześnie na połów dwa kutry: jeden na północ ze stałą prędkością 4 węzłów, drugi na wschód ze stałą prędkością 3 węzłów. Oblicz odległość między tymi kutrami po trzech godzinach od wypłynięcia. Wynik podaj w kilometrach. Zapisz obliczenia. 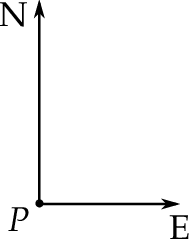
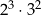 jest równa A/B.
jest równa A/B.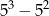 jest równa C/D.
jest równa C/D.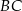 kwadratu
kwadratu 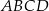 (na zewnątrz) zbudowano trójkąt równoboczny
(na zewnątrz) zbudowano trójkąt równoboczny 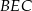 (zobacz rysunek).
(zobacz rysunek). 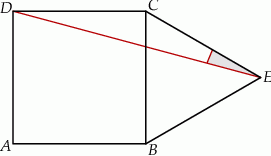
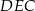 jest równa
jest równa 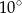
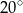
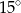
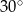
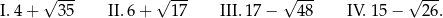
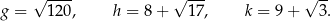
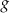 .
. 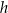 i
i 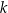 .
. 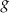 i
i 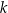 .
. 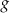 i
i 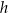 .
. 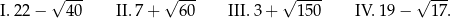
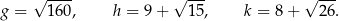
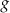 .
. 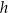 i
i 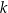 .
. 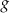 i
i 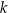 .
. 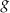 i
i 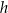 .
. 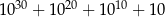 przez 12 jest równa
przez 12 jest równa 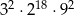
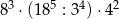
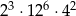
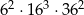
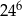 ?
? 