Na wykresie przedstawiono zależność pola pomalowanej powierzchni od ilości zużytej farby. Pole pomalowanej powierzchni jest wprost proporcjonalne do ilości zużytej farby.
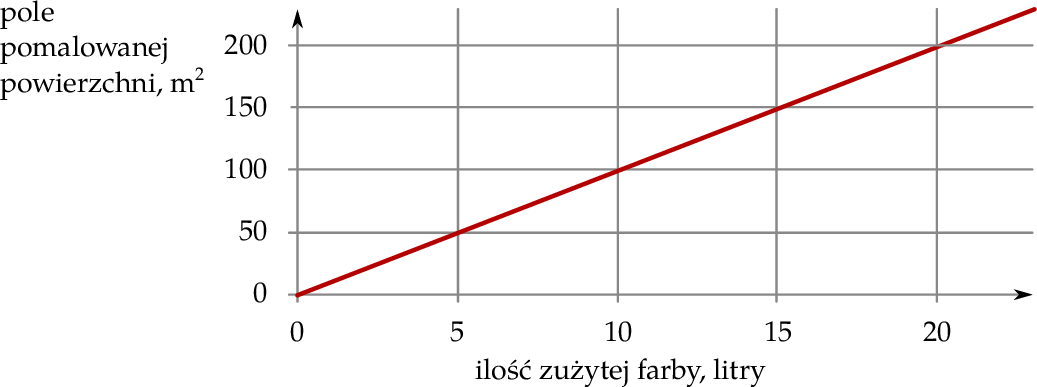
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
18 litrów tej farby wystarczy na pomalowanie 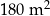 powierzchni. powierzchni. | P | F |
Na pomalowanie 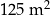 powierzchni wystarczy 12 litrów tej farby. powierzchni wystarczy 12 litrów tej farby. | P | F |

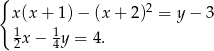
 .
. 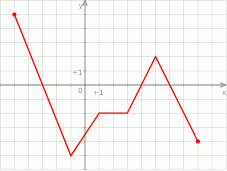
 dla trzech różnych argumentów.
dla trzech różnych argumentów.  dla więcej niż 3 różnych argumentów.
dla więcej niż 3 różnych argumentów. wartości funkcji są ujemne.
wartości funkcji są ujemne. 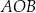 zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego
zaznaczonych na rysunkach, jeśli dana jest miara kąta wpisanego 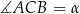 .
. 
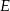 . Z punktu
. Z punktu 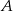 widziała ją pod kątem
widziała ją pod kątem 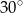 stopni do kierunku drogi. A z punktu
stopni do kierunku drogi. A z punktu 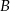 pod kątem
pod kątem 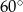 . Przejeżdżając przez punkt
. Przejeżdżając przez punkt 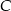 minęła elektrownię. Długość odcinka
minęła elektrownię. Długość odcinka 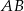 jest równa 20km.
jest równa 20km. 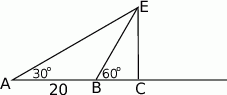
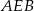 i
i 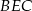 .
. 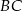 .
. 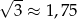 .
. 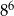 jest większa od liczby
jest większa od liczby 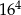
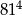 jest większa od liczby
jest większa od liczby 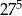
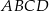 podzielono na 16 identycznych kwadratów (zobacz rysunek).
podzielono na 16 identycznych kwadratów (zobacz rysunek). 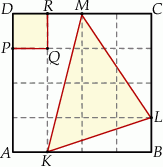
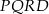 jest pole trójkąta
jest pole trójkąta 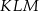 ?
?  i
i 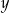 są dodatnie oraz
są dodatnie oraz 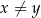 . Wyrażenie
. Wyrażenie 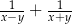 można przekształcić do postaci
można przekształcić do postaci 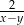
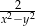
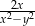
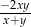
 i
i 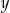 są dodatnie oraz
są dodatnie oraz 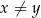 . Wyrażenie
. Wyrażenie 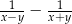 można przekształcić do postaci
można przekształcić do postaci 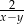
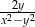
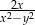
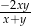
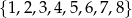 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 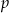 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy 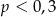
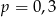
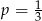
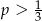
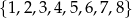 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 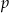 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy 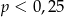
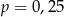
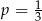
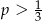
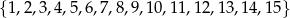 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 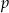 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas 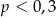
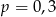
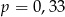
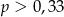
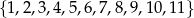 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 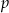 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas 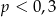
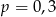
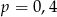
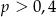
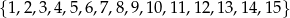 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 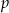 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas 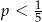
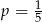
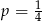
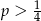
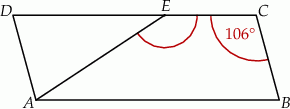
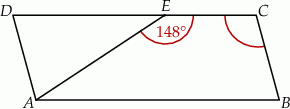
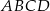 i trójkąt równoramienny
i trójkąt równoramienny 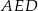 , w którym
, w którym 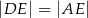 . Miara kąta
. Miara kąta 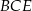 jest równa
jest równa 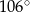 .
. 
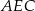 ?
? 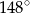
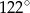
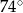
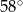
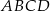 i trójkąt równoramienny
i trójkąt równoramienny 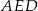 , w którym
, w którym 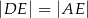 . Miara kąta
. Miara kąta 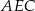 jest równa
jest równa 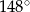 .
. 
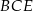 ?
? 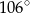
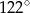
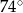
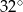
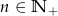 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba
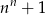
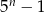
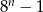
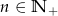 zawsze nieparzysta jest liczba
zawsze nieparzysta jest liczba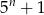
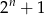
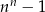
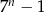
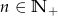 zawsze parzysta jest liczba
zawsze parzysta jest liczba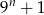
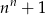
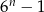
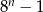
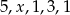 jest równa 3. Wtedy
jest równa 3. Wtedy 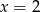
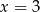
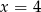
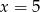
 średnia arytmetyczna liczb:
średnia arytmetyczna liczb: 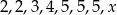 jest równa 4?
jest równa 4? 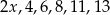 , jest równa 5. Wynika stąd, że
, jest równa 5. Wynika stąd, że 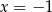
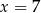
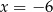
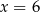
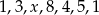 wynosi 4. Wynika z tego, że:
wynosi 4. Wynika z tego, że: 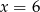
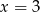
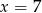
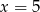
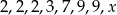 jest równa 4,5. Liczba
jest równa 4,5. Liczba  jest równa
jest równa 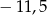
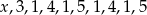 jest równa 3. Wtedy
jest równa 3. Wtedy 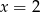
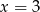
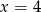
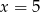
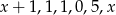 jest równa
jest równa  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa


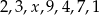 wynosi
wynosi 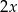 . Wynika z tego, że:
. Wynika z tego, że: 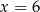
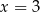
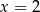
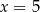
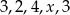 jest równa 3,2. Wtedy
jest równa 3,2. Wtedy 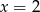
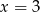
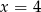
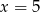
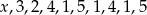 jest równa 3. Wtedy
jest równa 3. Wtedy 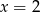
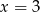
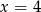
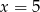
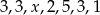 jest równa 3. Wtedy
jest równa 3. Wtedy 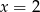
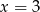
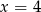
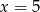
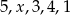 jest równa 3. Wtedy
jest równa 3. Wtedy 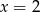
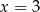
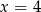
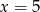
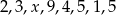 wynosi 4,5. Wynika z tego, że:
wynosi 4,5. Wynika z tego, że: 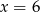
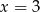
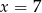
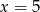
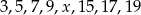 jest równa 11. Wtedy
jest równa 11. Wtedy 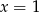
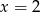
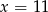
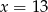
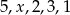 jest równa 3. Wtedy
jest równa 3. Wtedy 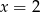
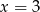
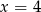
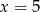
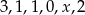 jest równa 2. Wtedy liczba
jest równa 2. Wtedy liczba  jest równa
jest równa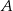 i
i 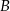 czworokąta
czworokąta 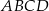 . Osie układu współrzędnych są osiami symetrii tego czworokąta.
. Osie układu współrzędnych są osiami symetrii tego czworokąta. 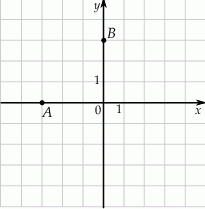
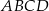 jest równe
jest równe 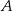 i
i 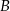 czworokąta
czworokąta 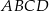 . Osie układu współrzędnych są osiami symetrii tego czworokąta.
. Osie układu współrzędnych są osiami symetrii tego czworokąta. 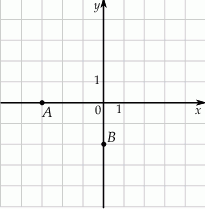
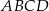 jest równe
jest równe 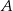 i
i 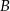 rombu
rombu  oraz jedną z jego osi symetrii.
oraz jedną z jego osi symetrii. 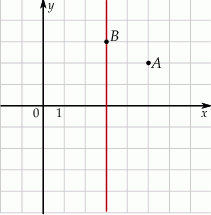
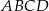 jest równe
jest równe 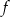 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 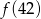 ,
, 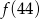 ,
, 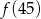 ,
, 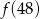 największa to
największa to 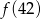
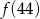
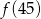
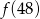
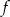 przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb:
przyporządkowuje każdej liczbie naturalnej większej od 1 jej największy dzielnik będący liczbą pierwszą. Spośród liczb: 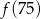 ,
, 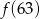 ,
, 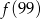 ,
, 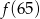 największa to
największa to 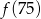
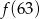
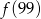
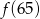
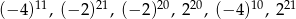 .
.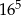 .
. 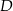 i
i 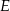 są środkami boków
są środkami boków 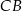 i
i 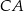 trójkąta
trójkąta 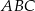 (zobacz rysunek). Wykaż, że odległość punktu
(zobacz rysunek). Wykaż, że odległość punktu 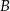 od prostej
od prostej 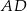 jest dwa razy większa od odległości punktu
jest dwa razy większa od odległości punktu 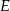 od prostej
od prostej 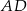 .
.