Oblicz pole trójkąta utworzonego przez osie układu współrzędnych i przez prostą o ujemnym współczynniku kierunkowym 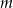 do której należy punkt
do której należy punkt 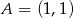 . Dla jakiej wartości
. Dla jakiej wartości 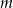 pole tego trójkąta jest najmniejsze?
pole tego trójkąta jest najmniejsze?
/Szkoła średnia/Geometria/Geometria analityczna
Dany jest okrąg o równaniu 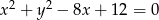 .
.
- Wyznacz równania stycznych do okręgu przechodzących przez początek układu współrzędnych.
- Oblicz pole figury ograniczonej stycznymi i łukiem okręgu wyznaczonym przez punkty styczności.
Z punktu 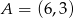 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 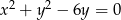 .
.
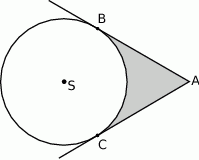
- Wyznacz równania tych stycznych.
- Oblicz odległość punktów styczności.
- Oblicz pole figury zaznaczonej na rysunku.
W kartezjańskim układzie współrzędnych 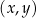 czworokąt
czworokąt 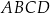 jest równoległobokiem takim, że
jest równoległobokiem takim, że ![−→ BD = [− 21,− 7]](https://img.zadania.info/zad/8179651/HzadT2x.png) i
i ![−→ DC = [15,8 ]](https://img.zadania.info/zad/8179651/HzadT3x.png) . Oblicz pole tego równoległoboku.
. Oblicz pole tego równoległoboku.
W okrąg o równaniu 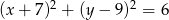 wpisano kwadrat. Oblicz pole tego kwadratu.
wpisano kwadrat. Oblicz pole tego kwadratu.
W czworokącie 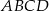 dane są
dane są ![−→ −→ AB = [6,− 3], DA = [− 8,− 7]](https://img.zadania.info/zad/8185465/HzadT1x.gif) oraz środek
oraz środek 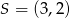 przekątnej
przekątnej 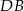 . Wyznacz współrzędne rzutu prostopadłego punktu
. Wyznacz współrzędne rzutu prostopadłego punktu 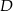 na prostą
na prostą 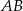 .
.
Punkty 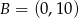 i
i 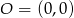 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 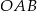 , w którym
, w którym 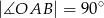 . Przyprostokątna
. Przyprostokątna 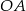 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 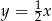 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 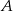 i długość przyprostokątnej
i długość przyprostokątnej 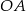 .
.
Dla jakich wartości parametru 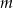 punkt przecięcia się prostych
punkt przecięcia się prostych 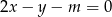 i
i 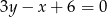 należy do prostej
należy do prostej 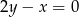 . Podaj współrzędne tego punktu i oblicz jego odległość od prostej
. Podaj współrzędne tego punktu i oblicz jego odległość od prostej 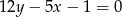 .
.
Określ wzajemne położenie prostych
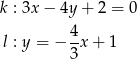
Dane są punkty 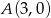 i
i 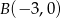 . Wyznacz równanie krzywej, utworzonej przez wszystkie punkty płaszczyzny, których odległość od punktu
. Wyznacz równanie krzywej, utworzonej przez wszystkie punkty płaszczyzny, których odległość od punktu 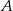 jest 2 razy większa od odległości od punktu
jest 2 razy większa od odległości od punktu 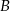 . Jaką figurę opisuje ta krzywa?
. Jaką figurę opisuje ta krzywa?
Dany jest okrąg o równaniu 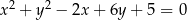 .
.
- Napisz równania stycznych do danego okręgu, prostopadłych do prostej o równaniu
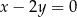 .
. - Oblicz pole trójkąta
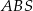 , gdzie
, gdzie 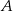 i
i 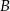 są punktami przecięcia się stycznych z prostą o równaniu
są punktami przecięcia się stycznych z prostą o równaniu 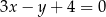 , zaś
, zaś 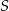 jest środkiem danego okręgu.
jest środkiem danego okręgu.
Wierzchołkami trójkąta 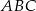 są środki okręgów określonych równaniami
są środki okręgów określonych równaniami 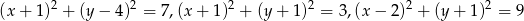 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
W układzie współrzędnych dany jest okrąg  opisany równaniem
opisany równaniem 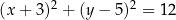 . Sprawdź, czy prosta o równaniu
. Sprawdź, czy prosta o równaniu 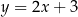 jest styczna do okręgu
jest styczna do okręgu  .
.
Wyznacz wszystkie wartości parametru 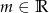 , dla których równanie
, dla których równanie
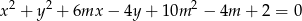
opisuje okrąg. Jaka jest największa możliwa długość tego okręgu?
Przekątne prostokąta 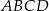 o polu
o polu 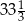 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 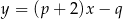 i
i 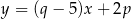 . Ponadto prosta
. Ponadto prosta 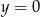 jest osią symetrii tego prostokąta. Oblicz obwód tego prostokąta.
jest osią symetrii tego prostokąta. Oblicz obwód tego prostokąta.
Przekątne prostokąta 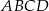 o obwodzie
o obwodzie 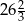 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 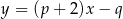 i
i 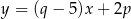 . Ponadto prosta
. Ponadto prosta 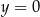 jest osią symetrii tego prostokąta. Oblicz pole tego prostokąta.
jest osią symetrii tego prostokąta. Oblicz pole tego prostokąta.
Dane są punkty 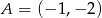 i
i 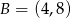 . Wyznacz te punkty prostej
. Wyznacz te punkty prostej 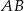 , dla których różnica odległości od punktu
, dla których różnica odległości od punktu 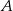 i odległości od punktu
i odległości od punktu 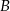 jest większa niż odległość od punktu
jest większa niż odległość od punktu 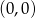 .
.
Oblicz odległość punktu 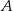 od środka odcinka
od środka odcinka 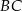 , gdzie
, gdzie 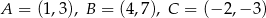 .
.
Oblicz odległość od początku układu współrzędnych środka odcinka 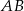 , gdzie
, gdzie 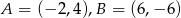 .
.
Oblicz odległość punktu 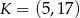 od środka odcinka o końcach
od środka odcinka o końcach 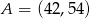 ,
, 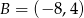 .
.
Oblicz odległość punktu 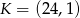 od środka odcinka o końcach
od środka odcinka o końcach 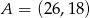 ,
, 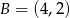 .
.
Punkty 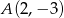 i
i 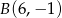 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 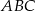 , którego pole jest równe 10. Wyznacz współrzędne wierzchołka
, którego pole jest równe 10. Wyznacz współrzędne wierzchołka 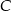 .
.
Odcinek 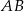 , gdzie
, gdzie 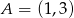 i
i 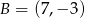 , jest podstawą trójkąta
, jest podstawą trójkąta 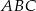 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 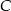 tak, aby trójkąt
tak, aby trójkąt 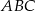 był równoramienny, a jego pole było równe 30.
był równoramienny, a jego pole było równe 30.
Prosta 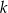 tworzy z dodatnią półosią
tworzy z dodatnią półosią 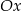 kąt o mierze
kąt o mierze 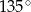 i przechodzi przez punkt
i przechodzi przez punkt 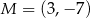 . Prosta
. Prosta 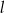 jest prostopadła do prostej
jest prostopadła do prostej 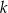 i przecina oś
i przecina oś 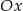 w punkcie o odciętej
w punkcie o odciętej 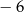 . Oblicz obwód trójkąta utworzonego przez proste
. Oblicz obwód trójkąta utworzonego przez proste 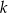 ,
, 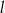 i oś
i oś 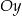 .
.
W parku krajobrazowym znajduje się zbiornik wodny, którego dwa brzegi postanowiono połączyć pomostem. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej zbiornika w kartezjańskim układzie współrzędnych 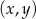 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 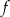 oraz
oraz 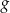 , które odpowiadają przeciwległym brzegom zbiornika (zobacz rysunek).
, które odpowiadają przeciwległym brzegom zbiornika (zobacz rysunek).
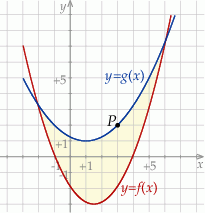
Funkcje 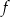 oraz
oraz 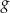 są określone wzorami
są określone wzorami 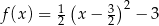 oraz
oraz 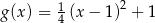 . Jeden z końców pomostu postanowiono zlokalizować na brzegu opisanym funkcją
. Jeden z końców pomostu postanowiono zlokalizować na brzegu opisanym funkcją 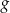 w punkcie o współrzędnych
w punkcie o współrzędnych 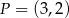 . Koniec pomostu należy umieścić na brzegu opisanym funkcją
. Koniec pomostu należy umieścić na brzegu opisanym funkcją 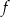 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 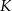 , w którym należy zlokalizować koniec pomostu, aby jego długość (tj. odległość końca
, w którym należy zlokalizować koniec pomostu, aby jego długość (tj. odległość końca 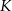 pomostu od początku
pomostu od początku 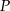 ) była możliwie najmniejsza. Oblicz długość najkrótszego pomostu.
) była możliwie najmniejsza. Oblicz długość najkrótszego pomostu.
Przy rozwiązywaniu zadania możesz skorzystać z tego, że odległość dowolnego punktu 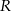 leżącego na wykresie funkcji
leżącego na wykresie funkcji 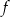 od punktu
od punktu 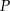 wyraża się wzorem
wyraża się wzorem
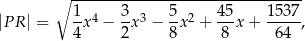
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 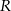 .
.
Wyznacz równanie okręgu stycznego do osi 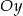 , którego środkiem jest punkt
, którego środkiem jest punkt 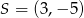 .
.

