Znajdź zbiór środków wszystkich cięciw okręgu 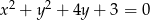 , wyznaczonych przez proste przechodzące przez punkt
, wyznaczonych przez proste przechodzące przez punkt 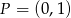 .
.
/Szkoła średnia/Geometria/Geometria analityczna
Punkty 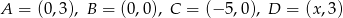 , gdzie
, gdzie 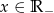 są kolejnymi wierzchołkami czworokąta
są kolejnymi wierzchołkami czworokąta 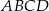 . Oblicz wartość
. Oblicz wartość  , dla której w czworokąt
, dla której w czworokąt 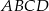 można wpisać okrąg.
można wpisać okrąg.
Znajdź równania prostych stycznych do dwóch okręgów: 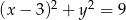 i
i 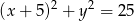 .
.
Wyznacz punkt wspólny symetralnej odcinka 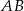 , gdzie
, gdzie 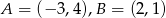 , oraz osi
, oraz osi 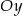 .
.
Punkt 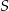 jest punktem przecięcia się przekątnych równoległoboku
jest punktem przecięcia się przekątnych równoległoboku 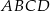 , a punkt
, a punkt 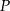 jest takim punktem boku
jest takim punktem boku 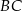 tego równoległoboku, że
tego równoległoboku, że 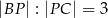 . Oblicz współrzędne spodka wysokości opuszczonej z wierzchołka
. Oblicz współrzędne spodka wysokości opuszczonej z wierzchołka 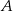 tego równoległoboku na prostą
tego równoległoboku na prostą 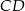 , jeżeli
, jeżeli ![−→ AB = [4,4]](https://img.zadania.info/zad/7923031/HzadT7x.gif) ,
, ![−→ DS = [3,− 3]](https://img.zadania.info/zad/7923031/HzadT8x.gif) i
i 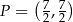 .
.
Okrąg o równaniu 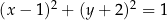 przecina jedną z gałęzi hiperboli o równaniu
przecina jedną z gałęzi hiperboli o równaniu 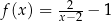 , gdzie
, gdzie 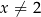 , w punktach
, w punktach 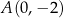 i
i 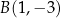 .
.
-
Narysuj obie krzywe we wspólnym układzie współrzędnych.
-
Na drugiej gałęzi hiperboli wyznacz współrzędne takiego punktu
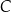 , który jest równo odległy od punktów
, który jest równo odległy od punktów 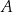 i
i 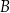 .
.
W trójkącie równoramiennym 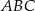 dane są wierzchołki podstawy:
dane są wierzchołki podstawy: 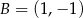 i
i 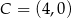 . Jedno z ramion trójkąta zawiera się w prostej o równaniu
. Jedno z ramion trójkąta zawiera się w prostej o równaniu 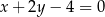 . Na boku
. Na boku 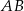 tego trójkąta obrano taki punkt
tego trójkąta obrano taki punkt 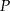 , że
, że 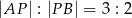 . Napisz równanie okręgu o środku w punkcie
. Napisz równanie okręgu o środku w punkcie 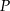 , stycznego do podstawy
, stycznego do podstawy 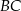 .
.
Dane są punkty 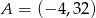 i
i 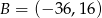 . Wykaż, że koło o średnicy
. Wykaż, że koło o średnicy 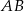 jest zawarte w II ćwiartce prostokątnego układu współrzędnych.
jest zawarte w II ćwiartce prostokątnego układu współrzędnych.
Punkty 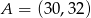 i
i 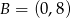 są sąsiednimi wierzchołkami czworokąta
są sąsiednimi wierzchołkami czworokąta 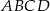 wpisanego w okrąg. Prosta o równaniu
wpisanego w okrąg. Prosta o równaniu 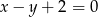 jest jedyną osią symetrii tego czworokąta i zawiera przekątną
jest jedyną osią symetrii tego czworokąta i zawiera przekątną 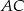 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 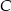 i
i 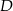 tego czworokąta.
tego czworokąta.
Punkty 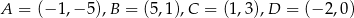 są kolejnymi wierzchołkami trapezu
są kolejnymi wierzchołkami trapezu 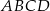 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Dane są figury:
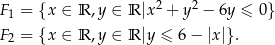
- Narysuj figury
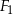 i
i 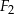 oraz wyznacz figurę
oraz wyznacz figurę 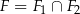 .
. - Oblicz pole figury
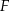
Dane są figury:
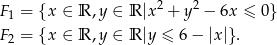
- Narysuj figury
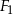 i
i 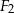 oraz wyznacz figurę
oraz wyznacz figurę 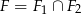 .
. - Oblicz pole figury
Punkty 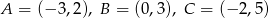 to wierzchołki trójkąta. Podaj, jakie są współrzędne wierzchołków trójkąta symetrycznego do trójkąta
to wierzchołki trójkąta. Podaj, jakie są współrzędne wierzchołków trójkąta symetrycznego do trójkąta 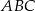 względem
względem
- osi
 ,
, - osi
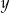 ,
, - punktu
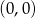 .
.
Wyznacz równanie okręgu wpisanego w kwadrat 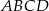 , gdzie
, gdzie 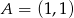 i
i 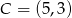 .
.
Wyznacz równanie okręgu opisanego na prostokącie 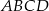 , w którym
, w którym 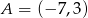 i
i 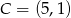 .
.
Dane są punkty 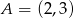 i
i 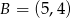 . Na prostej o równaniu
. Na prostej o równaniu 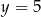 wyznacz punkt
wyznacz punkt 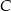 tak, aby łamana
tak, aby łamana 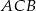 miała jak najmniejszą długość. Odpowiedź uzasadnij.
miała jak najmniejszą długość. Odpowiedź uzasadnij.
Dane są punkty 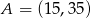 i
i 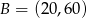 . Wyznacz współrzędne punktu przecięcia prostej
. Wyznacz współrzędne punktu przecięcia prostej 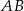 z osią
z osią 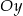 .
.
Okrąg jest styczny do osi układu współrzędnych w punktach 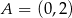 i
i 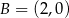 oraz jest styczny do prostej
oraz jest styczny do prostej 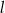 w punkcie
w punkcie 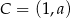 , gdzie
, gdzie 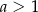 . Wyznacz równanie prostej
. Wyznacz równanie prostej 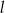 .
.
Okrąg jest styczny do osi układu współrzędnych w punktach 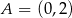 i
i 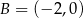 oraz jest styczny do prostej
oraz jest styczny do prostej 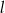 w punkcie
w punkcie 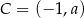 , gdzie
, gdzie 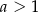 . Wyznacz równanie prostej
. Wyznacz równanie prostej 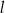 .
.
Rozważmy cięciwy 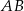 paraboli
paraboli 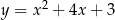 przechodzące przez punkt
przechodzące przez punkt 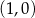 , przy czym przez cięciwę
, przy czym przez cięciwę 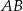 rozumiemy prostą przecinającą tę parabolę w dwóch punktach
rozumiemy prostą przecinającą tę parabolę w dwóch punktach 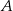 i
i 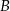 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 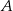 i
i 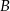 , dla których suma współrzędnych środka odcinka
, dla których suma współrzędnych środka odcinka 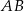 cięciwy
cięciwy 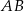 jest równa
jest równa 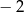 .
.
Punkt 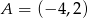 oraz
oraz 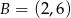 są symetryczne względem prostej
są symetryczne względem prostej 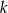 . Wyznacz równanie prostej
. Wyznacz równanie prostej 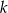 .
.
Punkt 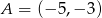 oraz
oraz 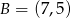 są symetryczne względem prostej
są symetryczne względem prostej 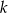 . Wyznacz równanie prostej
. Wyznacz równanie prostej 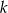 .
.
Oblicz pole trójkąta utworzonego przez osie układu współrzędnych i przez prostą o ujemnym współczynniku kierunkowym 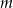 do której należy punkt
do której należy punkt 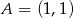 . Dla jakiej wartości
. Dla jakiej wartości 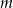 pole tego trójkąta jest najmniejsze?
pole tego trójkąta jest najmniejsze?

