Na obrzeżach miasta znajduje się jezioro, na którym postanowiono stworzyć tor regatowy. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej jeziora w kartezjańskim układzie współrzędnych 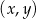 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 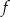 oraz
oraz 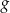 (zobacz rysunek).
(zobacz rysunek).
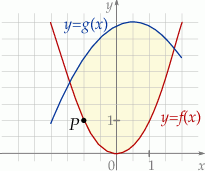
Funkcje 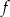 oraz
oraz 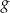 są określone wzorami
są określone wzorami 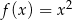 oraz
oraz 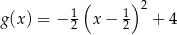 . Początek toru postanowiono zlokalizować na brzegu jeziora w miejscu, któremu odpowiada w układzie współrzędnych punkt
. Początek toru postanowiono zlokalizować na brzegu jeziora w miejscu, któremu odpowiada w układzie współrzędnych punkt 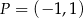 . Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu
. Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu 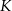 , w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca
, w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca 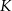 toru od początku
toru od początku 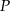 ) była możliwie największa. Oblicz długość najdłuższego toru.
) była możliwie największa. Oblicz długość najdłuższego toru.
Przy rozwiązywaniu zadania możesz skorzystać z tego, że odległość dowolnego punktu 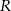 leżącego na wykresie funkcji
leżącego na wykresie funkcji 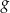 od punktu
od punktu 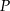 wyraża się wzorem
wyraża się wzorem
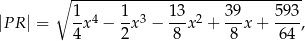
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 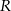 .
.

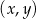 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 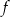 oraz
oraz 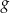 (zobacz rysunek).
(zobacz rysunek). 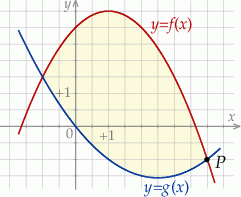
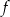 oraz
oraz 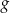 są określone wzorami
są określone wzorami 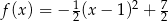 oraz
oraz 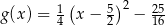 . Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt
. Początek toru postanowiono zlokalizować na brzegu w miejscu, któremu odpowiada w układzie współrzędnych punkt 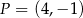 . Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu
. Koniec toru regatowego należy umieścić na linii brzegowej. Oblicz współrzędne punktu 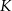 , w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca
, w którym należy zlokalizować koniec toru, aby długość toru (tj. odległość końca 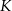 toru od początku
toru od początku 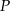 ) była możliwie największa. Oblicz długość najdłuższego toru.
) była możliwie największa. Oblicz długość najdłuższego toru. 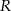 leżącego na wykresie funkcji
leżącego na wykresie funkcji 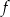 od punktu
od punktu 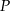 wyraża się wzorem
wyraża się wzorem 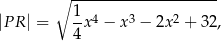
 jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 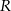 .
. 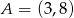 i
i 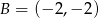 prostokąta
prostokąta 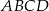 oraz punkt
oraz punkt 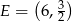 leżący na prostej
leżący na prostej 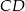 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 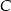 i
i 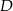 tego prostokąta.
tego prostokąta. 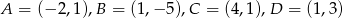 .
. 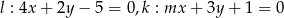 . Wyznacz parametr
. Wyznacz parametr 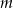 , tak aby te proste były prostopadłe.
, tak aby te proste były prostopadłe. 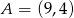 . Na okręgu o równaniu
. Na okręgu o równaniu 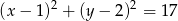 wyznacz współrzędne punktu
wyznacz współrzędne punktu 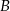 , dla którego odległość
, dla którego odległość 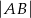 jest największa.
jest największa. 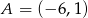 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 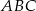 , a punkt
, a punkt 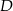 jest środkiem odcinka
jest środkiem odcinka 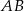 . Równania prostych
. Równania prostych 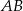 ,
, 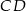 oraz symetralnej boku
oraz symetralnej boku 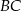 to odpowiednio
to odpowiednio 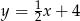 ,
, 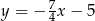 i
i 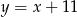 . Napisz równanie prostej zawierającej wysokość trójkąta
. Napisz równanie prostej zawierającej wysokość trójkąta 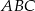 opuszczoną z wierzchołka
opuszczoną z wierzchołka 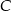 .
. 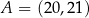 i
i 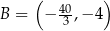 są końcami przeciwprostokątnej trójkąta prostokątnego
są końcami przeciwprostokątnej trójkąta prostokątnego 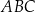 . Punkt
. Punkt 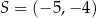 jest środkiem okręgu wpisanego w ten trójkąt. Oblicz pole trójkąta
jest środkiem okręgu wpisanego w ten trójkąt. Oblicz pole trójkąta 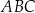 .
. 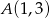 leży na dwusiecznej kąta między prostymi
leży na dwusiecznej kąta między prostymi 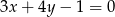 i
i 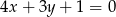 . Napisz równanie tej dwusiecznej.
. Napisz równanie tej dwusiecznej. 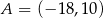 . Prosta o równaniu
. Prosta o równaniu 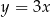 jest symetralną odcinka
jest symetralną odcinka 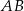 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 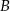 .
. 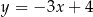 jest symetralną odcinka
jest symetralną odcinka 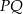 , gdzie
, gdzie 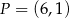 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 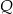 .
. 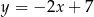 jest symetralną odcinka
jest symetralną odcinka 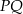 , gdzie
, gdzie 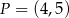 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 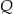 .
. 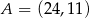 . Prosta o równaniu
. Prosta o równaniu 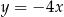 jest symetralną odcinka
jest symetralną odcinka 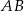 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 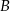 .
. 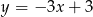 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 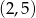 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania. 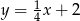 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt
. Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 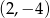 . Wykonaj rysunek do zadania.
. Wykonaj rysunek do zadania. 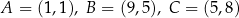 .
. 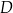 tak, aby czworokąt
tak, aby czworokąt 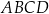 był trapezem prostokątnym, którego kąt przy wierzchołku
był trapezem prostokątnym, którego kąt przy wierzchołku 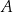 jest prosty.
jest prosty. 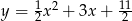 . Oblicz pole tego trójkąta. Rozważ wszystkie możliwe przypadki.
. Oblicz pole tego trójkąta. Rozważ wszystkie możliwe przypadki. 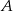 na prostej
na prostej 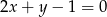 , by suma kwadratów jego odległości od osi układu była najmniejsza.
, by suma kwadratów jego odległości od osi układu była najmniejsza. 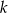 przechodzi przez punkty
przechodzi przez punkty 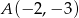 i
i 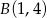 . Wyznacz równania prostej
. Wyznacz równania prostej 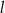 prostopadłej do
prostopadłej do 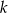 i prostej
i prostej 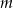 równoległej do
równoległej do 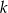 , jeżeli każda z nich przechodzi przez punkt
, jeżeli każda z nich przechodzi przez punkt 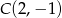 .
. 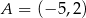 i
i 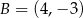 są wierzchołkami trójkąta
są wierzchołkami trójkąta 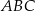 , a wysokości opuszczone z wierzchołków
, a wysokości opuszczone z wierzchołków 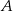 i
i 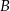 tego trójkąta zawierają się odpowiednio w prostych o równaniach
tego trójkąta zawierają się odpowiednio w prostych o równaniach 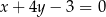 oraz
oraz 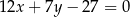 . Oblicz długość wysokości tego trójkąta opuszczonej na bok
. Oblicz długość wysokości tego trójkąta opuszczonej na bok 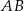 .
. 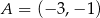 i
i 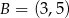 są wierzchołkami trójkąta
są wierzchołkami trójkąta 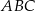 , a jego wysokości przecinają się w punkcie
, a jego wysokości przecinają się w punkcie 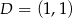 . Oblicz długość wysokości tego trójkąta opuszczonej na bok
. Oblicz długość wysokości tego trójkąta opuszczonej na bok 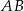 .
. 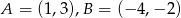 . Wyznacz taki punkt
. Wyznacz taki punkt 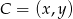 , gdzie
, gdzie 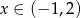 leżący na paraboli o równaniu
leżący na paraboli o równaniu 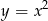 , aby pole trójkąta
, aby pole trójkąta 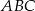 było największe.
było największe.  ma środek
ma środek 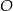 i jest styczny prostej
i jest styczny prostej 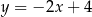 w punkcie
w punkcie 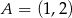 . Wyznacz równanie okręgu
. Wyznacz równanie okręgu  , jeżeli
, jeżeli ![−→ OA = [2,1]](https://img.zadania.info/zad/7820974/HzadT5x.gif) .
. 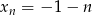 dla
dla 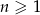 . Ciąg
. Ciąg 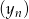 ma tę własność, że dla każdego
ma tę własność, że dla każdego 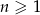 punkty o współrzędnych
punkty o współrzędnych 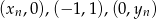 leżą na jednej prostej. Wyznacz wzór ogólny ciągu
leżą na jednej prostej. Wyznacz wzór ogólny ciągu 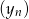 .
. 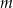 , dla której pole koła stycznego do prostych zawierających boki
, dla której pole koła stycznego do prostych zawierających boki 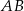 i
i 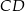 równoległoboku
równoległoboku 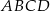 o wierzchołkach
o wierzchołkach 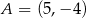 ,
, 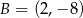 ,
, 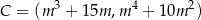 jest najmniejsze możliwe. Oblicz to pole.
jest najmniejsze możliwe. Oblicz to pole. 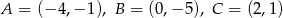 są wierzchołkami trójkąta równoramiennego. Wyznacz równanie osi symetrii tego trójkąta.
są wierzchołkami trójkąta równoramiennego. Wyznacz równanie osi symetrii tego trójkąta. 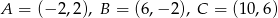 .
. 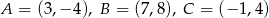 .
. 