Zapisz równanie prostej przechodzącej przez punkt 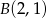 i prostopadłej do prostej danej równaniem
i prostopadłej do prostej danej równaniem 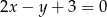 .
.
/Szkoła średnia/Geometria/Geometria analityczna
Wyznacz równanie prostej prostopadłej do prostej o równaniu 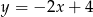 przecinającej oś
przecinającej oś 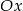 w punkcie o odciętej 4.
w punkcie o odciętej 4.
Zapisz równanie prostej przechodzącej przez punkt 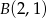 i prostopadłej do prostej danej równaniem
i prostopadłej do prostej danej równaniem 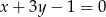 .
.
Wyznacz równanie prostej prostopadłej do prostej 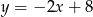 przechodzącej przez punkt
przechodzącej przez punkt 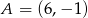 .
.
Wyznacz równanie prostej prostopadłej do prostej o równaniu 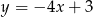 przechodzącej przez punkt
przechodzącej przez punkt 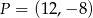 .
.
Punkty 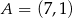 i
i 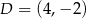 są kolejnymi wierzchołkami trapezu równoramiennego
są kolejnymi wierzchołkami trapezu równoramiennego 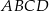 . Podstawa
. Podstawa 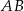 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 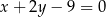 . Osią symetrii tego trapezu jest prosta o równaniu
. Osią symetrii tego trapezu jest prosta o równaniu 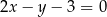 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 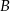 i
i 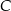 trapezu.
trapezu.
Wykaż, że czworokąt o wierzchołkach 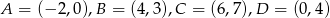 jest trapezem.
jest trapezem.
Prosta o równaniu 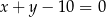 przecina okrąg o równaniu
przecina okrąg o równaniu 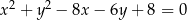 w punktach
w punktach 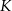 i
i 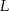 . Punkt
. Punkt 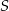 jest środkiem cięciwy
jest środkiem cięciwy 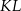 . Wyznacz równanie obrazu tego okręgu w jednokładności o środku
. Wyznacz równanie obrazu tego okręgu w jednokładności o środku 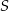 i skali
i skali 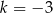 .
.
Sprawdź czy proste  i
i 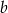 są równoległe, jeśli prosta
są równoległe, jeśli prosta  przecina oś
przecina oś  w punkcie
w punkcie 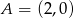 , oś
, oś 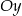 w punkcie
w punkcie 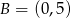 , a prosta
, a prosta 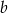 przecina oś
przecina oś 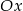 w punkcie
w punkcie 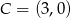 i oś
i oś 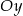 w punkcie
w punkcie 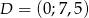 .
.
Każdy z wierzchołków trójkąta prostokątnego 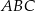 leży na na wykresie funkcji
leży na na wykresie funkcji 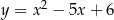 . Bok
. Bok 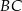 tego trójkąta jest zawarty w prostej
tego trójkąta jest zawarty w prostej 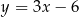 , a wierzchołek
, a wierzchołek 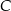 kąta prostego ma obie współrzędne dodatnie. Oblicz pole trójkąta
kąta prostego ma obie współrzędne dodatnie. Oblicz pole trójkąta 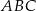 .
.
Okrąg o środku w punkcie 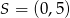 ma promień długości 1 i jest styczny do okręgu o środku
ma promień długości 1 i jest styczny do okręgu o środku 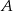 i promieniu długości 10. Punkt
i promieniu długości 10. Punkt 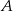 leży na osi
leży na osi 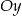 . Jakie ma współrzędne?
. Jakie ma współrzędne?
Znajdź równanie okręgu przechodzącego przez punkt 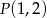 i stycznego jednocześnie do prostych
i stycznego jednocześnie do prostych 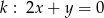 i
i 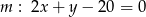 .
.
Dane są dwa nieskończone ciągi 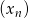 i
i 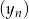 takie, że dla każdego
takie, że dla każdego 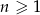 , punkt o współrzędnych
, punkt o współrzędnych 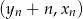 jest środkiem ciężkości trójkąta o wierzchołkach
jest środkiem ciężkości trójkąta o wierzchołkach 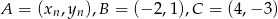 . Wyznacz wzory ciągów
. Wyznacz wzory ciągów 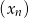 i
i 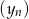 .
.
Proste o równaniach 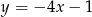 i
i 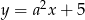 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Proste o równaniach 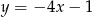 i
i 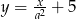 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Proste o równaniach 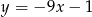 i
i 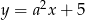 są prostopadłe. Wyznacz liczbę
są prostopadłe. Wyznacz liczbę  .
.
Wierzchołek 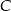 trójkąta ostrokątnego
trójkąta ostrokątnego 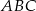 ma współrzędne
ma współrzędne 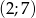 . Prosta o równaniu
. Prosta o równaniu 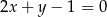 jest symetralną wysokości
jest symetralną wysokości 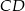 , a prosta o równaniu
, a prosta o równaniu 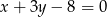 zawiera środkową trójkąta poprowadzoną z wierzchołka
zawiera środkową trójkąta poprowadzoną z wierzchołka 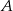 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 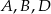 .
.
Napisz równanie okręgu stycznego do osi 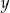 w punkcie
w punkcie 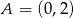 i przechodzącego przez punkt
i przechodzącego przez punkt 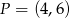 . Wyznacz na okręgu takie punkty
. Wyznacz na okręgu takie punkty 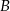 i
i 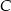 , aby trójkąt
, aby trójkąt 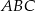 był równoboczny.
był równoboczny.
Wyznacz równanie okręgu stycznego wewnętrznie do okręgu o równaniu 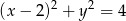 i do prostej
i do prostej 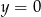 , którego środek ma współrzędne różnych znaków i leży na wykresie funkcji
, którego środek ma współrzędne różnych znaków i leży na wykresie funkcji 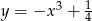 .
.
Przyprostokątna 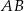 trójkąta prostokątnego
trójkąta prostokątnego 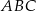 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 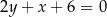 , a środek jego przeciwprostokątnej
, a środek jego przeciwprostokątnej 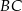 ma współrzędne
ma współrzędne 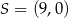 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 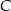 jeżeli
jeżeli 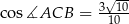 .
.
Wyznacz równanie prostej zawierającej środkową 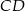 trójkąta
trójkąta 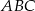 , którego wierzchołkami są punkty:
, którego wierzchołkami są punkty: 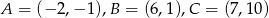 .
.
Punkty 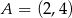 ,
, 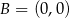 ,
, 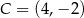 są wierzchołkami trójkąta
są wierzchołkami trójkąta 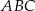 . Punkt
. Punkt 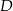 jest środkiem boku
jest środkiem boku 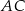 tego trójkąta. Wyznacz równanie prostej
tego trójkąta. Wyznacz równanie prostej 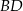 .
.
Wyznacz równanie prostej zawierającej środkową 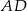 trójkąta
trójkąta 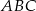 o wierzchołkach
o wierzchołkach 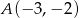 ,
, 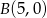 i
i 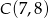 .
.
Wyznacz równanie prostej zawierającej środkową 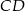 trójkąta
trójkąta 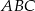 , którego wierzchołkami są punkty:
, którego wierzchołkami są punkty: 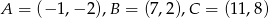 .
.
Oblicz obwód trójkąta o wierzchołkach: 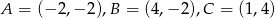 .
.
Oblicz obwód trójkąta o wierzchołkach: 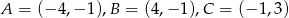 .
.
Ile punktów wspólnych ma okrąg o równaniu 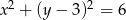 z prostą o równaniu
z prostą o równaniu 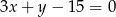 ?
?
Proste 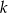 i
i 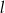 przecinają się w punkcie
przecinają się w punkcie 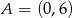 . Prosta
. Prosta 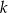 przecina ujemną półoś
przecina ujemną półoś 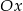 w punkcie
w punkcie 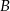 i tworzy z osiami układu trójkąt o polu 6, a prosta
i tworzy z osiami układu trójkąt o polu 6, a prosta 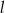 przecina dodatnią półoś
przecina dodatnią półoś 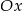 w punkcie
w punkcie 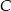 i tworzy z osiami układu trójkąt o polu 24. Oblicz długość wysokości trójkąta
i tworzy z osiami układu trójkąt o polu 24. Oblicz długość wysokości trójkąta 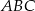 opuszczonej z wierzchołka
opuszczonej z wierzchołka 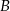 .
.
Punkt 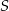 jest punktem przecięcia się środkowych trójkąta równoramiennego
jest punktem przecięcia się środkowych trójkąta równoramiennego 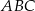 o podstawie
o podstawie 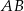 . Okrąg o średnicy
. Okrąg o średnicy 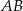 ma równanie
ma równanie 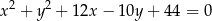 , a cięciwa tego okręgu równoległa do prostej
, a cięciwa tego okręgu równoległa do prostej 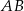 i przechodząca przez punkt
i przechodząca przez punkt 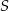 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 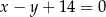 . Wyznacz równanie okręgu o środku
. Wyznacz równanie okręgu o środku 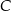 , który przechodzi przez punkty
, który przechodzi przez punkty 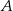 i
i 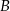 .
.
Prosta 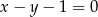 jest osią symetrii pewnego czworokąta wpisanego w okrąg. Punkty
jest osią symetrii pewnego czworokąta wpisanego w okrąg. Punkty 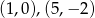 są jego wierzchołkami. Znajdź pozostałe wierzchołki.
są jego wierzchołkami. Znajdź pozostałe wierzchołki.

