Punkty 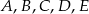 są kolejnymi wierzchołkami pięciokąta, w którym
są kolejnymi wierzchołkami pięciokąta, w którym ![→ → → → AB = [2 ,−3 ], AC = [6,− 2], ED = [3,− 1],CD = [0,4]](https://img.zadania.info/zad/6753416/HzadT1x.gif) . Znajdź współrzędne wektorów
. Znajdź współrzędne wektorów 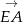 i
i 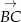 .
.
/Szkoła średnia/Geometria/Geometria analityczna
Punkt 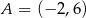 jest wierzchołkiem rombu
jest wierzchołkiem rombu 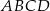 o polu 90. Przekątna
o polu 90. Przekątna 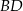 zawiera się w prostej
zawiera się w prostej 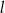 o równaniu
o równaniu 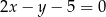 . Wyznacz długość boku tego rombu.
. Wyznacz długość boku tego rombu.
Punkty przecięcia paraboli 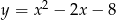 z prostą
z prostą 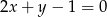 są końcami przekątnej rombu, którego pole wynosi 30. Oblicz współrzędne wierzchołków tego rombu oraz długość jego boku.
są końcami przekątnej rombu, którego pole wynosi 30. Oblicz współrzędne wierzchołków tego rombu oraz długość jego boku.
Wyznacz równanie okręgu wpisanego w deltoid, którego boki są zawarte w prostych o równaniach 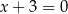 ,
, 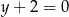 ,
, 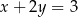 i
i 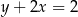 .
.
Wyznacz te wartości parametru 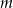 , dla których punkt przecięcia się prostych o równaniach
, dla których punkt przecięcia się prostych o równaniach 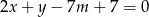 i
i 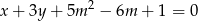 należy do 3 ćwiartki układu współrzędnych.
należy do 3 ćwiartki układu współrzędnych.
Punkty 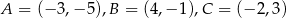 są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
Punkty 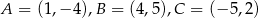 są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
są wierzchołkami trójkąta równoramiennego. Oblicz długość ramienia tego trójkąta.
Trójkąt jest rozpięty na wektorach 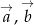 . Wyrazić środkowe tego trójkąta przez wektory
. Wyrazić środkowe tego trójkąta przez wektory 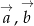 .
.
Na rysunku przedstawione są dwa wierzchołki trójkąta prostokątnego  :
: 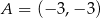 i
i 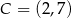 oraz prosta o równaniu
oraz prosta o równaniu 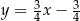 , zawierająca przeciwprostokątną
, zawierająca przeciwprostokątną 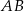 tego trójkąta.
tego trójkąta.
Oblicz współrzędne wierzchołka  tego trójkąta i długość odcinka
tego trójkąta i długość odcinka 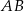 .
.
Na rysunku przedstawione są dwa wierzchołki trójkąta prostokątnego 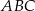 :
: 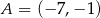 i
i 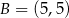 oraz prosta o równaniu
oraz prosta o równaniu 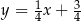 , zawierająca przeciwprostokątną
, zawierająca przeciwprostokątną 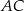 tego trójkąta.
tego trójkąta.
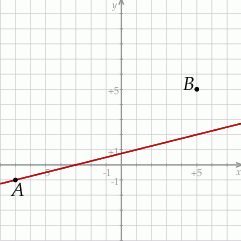
Oblicz współrzędne wierzchołka 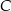 tego trójkąta i długość odcinka
tego trójkąta i długość odcinka 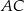 .
.
Sprawdź czy punkt 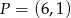 leży na dwusiecznej kąta
leży na dwusiecznej kąta 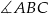 trójkąta o wierzchołkach
trójkąta o wierzchołkach 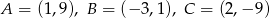 .
.
Dany jest okrąg o środku w punkcie 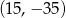 i promieniu 16. Sprawdź czy okrąg ten jest styczny do
i promieniu 16. Sprawdź czy okrąg ten jest styczny do
- prostej
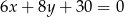 ,
, - okręgu o środku w punkcie
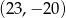 i promieniu 2?
i promieniu 2?
Uzasadnij swoją odpowiedź.
Sprawdź, czy czworokąt 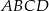 , gdzie
, gdzie 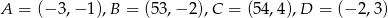 jest równoległobokiem. Odpowiedź uzasadnij.
jest równoległobokiem. Odpowiedź uzasadnij.
Dany jest trójkąt 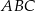 o wierzchołkach:
o wierzchołkach: 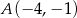 ,
, 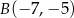 ,
, 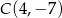 . Oblicz długość odcinka
. Oblicz długość odcinka 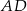 dwusiecznej kąta przy wierzchołku
dwusiecznej kąta przy wierzchołku 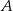 .
.
W układzie współrzędnych są dane punkty 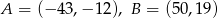 . Prosta
. Prosta 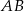 przecina oś
przecina oś 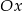 w punkcie
w punkcie 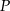 . Oblicz pierwszą współrzędną punktu
. Oblicz pierwszą współrzędną punktu 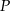 .
.
W układzie współrzędnych są dane punkty 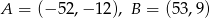 . Prosta
. Prosta 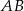 przecina oś
przecina oś 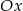 w punkcie
w punkcie 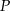 . Oblicz pierwszą współrzędną punktu
. Oblicz pierwszą współrzędną punktu 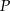 .
.
Dane są punkty 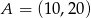 i
i 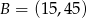 . Wyznacz współrzędne punktu przecięcia prostej
. Wyznacz współrzędne punktu przecięcia prostej 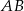 z osią
z osią 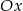 .
.
Narysuj w układzie współrzędnych obraz odcinka o końcach  w:
w:
- symetrii względem osi
 ;
; - symetrii względem osi
 ;
; - symetrii względem początku układu współrzędnych.
Napisz równanie okręgu o środku 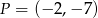 , którego punkty wspólne z okręgiem o równaniu
, którego punkty wspólne z okręgiem o równaniu 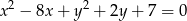 są końcami odcinka o długości
są końcami odcinka o długości 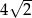 .
.
Dany jest okrąg 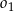 o równaniu
o równaniu 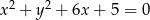 oraz okrąg
oraz okrąg 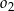 o równaniu
o równaniu 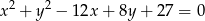 . Oblicz współrzędne środka jednokładności i skalę jednokładności, w której obrazem okręgu
. Oblicz współrzędne środka jednokładności i skalę jednokładności, w której obrazem okręgu 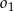 jest okrąg
jest okrąg 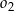 .
.
W układzie współrzędnych dane są punkty 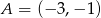 i
i 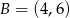 . Na wykresie funkcji
. Na wykresie funkcji 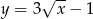 znajdź taki punkt
znajdź taki punkt 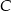 , dla którego pole trójkąta
, dla którego pole trójkąta 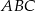 jest najmniejsze.
jest najmniejsze.
Wykaż, że cosinus kąta przecięcia się wykresów funkcji 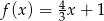 i
i 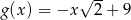 jest równy
jest równy 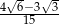 .
.
Dane są punkty 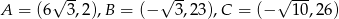 . Opisz za pomocą nierówności półpłaszczyznę o krawędzi
. Opisz za pomocą nierówności półpłaszczyznę o krawędzi 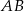 , do której należy punkt
, do której należy punkt 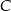 .
.
Wyznacz kąty trójkąta 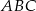 o wierzchołkach
o wierzchołkach 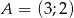 ,
, 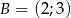 ,
, 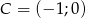 .
.

