Uzasadnij, że koło o środku 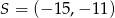 i promieniu
i promieniu 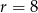 jest w całości zawarte w trójkącie o wierzchołkach
jest w całości zawarte w trójkącie o wierzchołkach 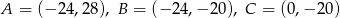 .
.
/Szkoła średnia/Geometria/Geometria analityczna
Punkty 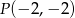 ,
, 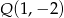 i
i 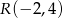 są środkami boków
są środkami boków 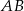 ,
, 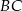 i
i 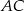 trójkąta
trójkąta 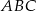 . Oblicz:
. Oblicz:
- Współrzędne wierzchołków trójkąta
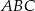 .
. - Obwód trójkąta
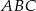 .
.
Znajdź równanie okręgu o środku w punkcie 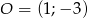 , wiedząc, że okrąg jest styczny do prostej
, wiedząc, że okrąg jest styczny do prostej 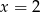 .
.
Punkty 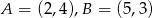 i
i 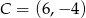 są sąsiednimi wierzchołkami czworokąta
są sąsiednimi wierzchołkami czworokąta 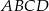 wpisanego w okrąg. Wierzchołek
wpisanego w okrąg. Wierzchołek 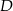 tego czworokąta leży na prostej o równaniu
tego czworokąta leży na prostej o równaniu 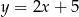 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 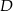 .
.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 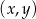 , dane są proste
, dane są proste 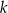 oraz
oraz 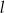 o równaniach
o równaniach
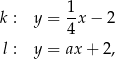
gdzie  jest pewną liczbą rzeczywistą. Proste
jest pewną liczbą rzeczywistą. Proste 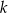 i
i 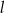 są prostopadłe. Wyznacz ich punkt przecięcia.
są prostopadłe. Wyznacz ich punkt przecięcia.
Rozstrzygnij czy trójkąt 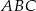 i trójkąt
i trójkąt 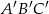 są przystające jeśli współrzędne ich wierzchołków to
są przystające jeśli współrzędne ich wierzchołków to 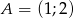 ,
, 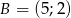 ,
, 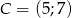 ,
, 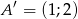 ,
, 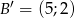 ,
, 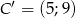 .
.
Na prostej 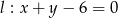 wyznacz taki punkt
wyznacz taki punkt 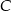 , aby długość łamanej
, aby długość łamanej 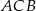 , gdzie
, gdzie 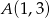 ,
, 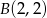 , była najmniejsza. Uzasadnij swoje rozumowanie.
, była najmniejsza. Uzasadnij swoje rozumowanie.
Rozważamy prostokąty, których dwa wierzchołki leżą na odcinku łączącym punkty wspólne osi 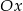 i paraboli o równaniu
i paraboli o równaniu 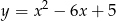 , a dwa należą do tej paraboli. Wyznacz współrzędne wierzchołków tego prostokąta, który ma największy obwód.
, a dwa należą do tej paraboli. Wyznacz współrzędne wierzchołków tego prostokąta, który ma największy obwód.
Oblicz pole czworokąta 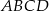 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 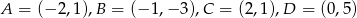 .
.
Oblicz pole czworokąta 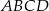 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 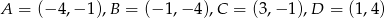 .
.
Środki okręgów 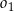 i
i 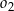 znajdują się po różnych stronach prostej
znajdują się po różnych stronach prostej 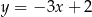 , która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu
, która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu 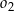 jest równy
jest równy 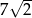 oraz, że okrąg
oraz, że okrąg 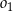 ma równanie
ma równanie 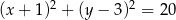 , wyznacz równanie okręgu
, wyznacz równanie okręgu 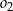 .
.
Dane są okrąg 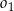 o równaniu
o równaniu 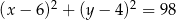 oraz okrąg
oraz okrąg 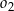 o promieniu
o promieniu 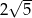 . Środki okręgów
. Środki okręgów 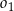 i
i 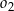 leżą po różnych stronach prostej
leżą po różnych stronach prostej 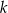 o równaniu
o równaniu 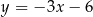 , a punkty wspólne obu okręgów leżą na prostej
, a punkty wspólne obu okręgów leżą na prostej 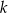 . Wyznacz równanie okręgu
. Wyznacz równanie okręgu 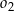 .
.
Określ wzajemne położenie prostych 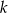 i
i 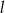 o równaniach
o równaniach
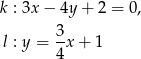
Na wykresie funkcji 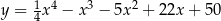 znajdź współrzędne punktu
znajdź współrzędne punktu 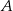 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 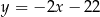 jest najmniejsza.
jest najmniejsza.
Na wykresie funkcji 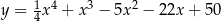 znajdź współrzędne punktu
znajdź współrzędne punktu 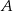 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 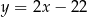 jest najmniejsza.
jest najmniejsza.
Udowodnij, że każdy punkt paraboli o równaniu 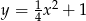 jest równoodległy od osi
jest równoodległy od osi 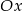 i od punktu
i od punktu 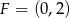 .
.
Dana jest parabola o równaniu 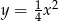 i punkt
i punkt 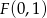 . Wykaż, że każdy punkt leżący na paraboli jest równo oddalony od punktu
. Wykaż, że każdy punkt leżący na paraboli jest równo oddalony od punktu 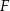 i prostej
i prostej 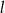 o równaniu
o równaniu 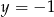 .
.
Punkty 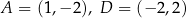 są kolejnymi wierzchołkami trapezu
są kolejnymi wierzchołkami trapezu 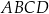 . Prosta
. Prosta 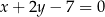 jest osią symetrii tego trapezu. Wyznacz współrzędne pozostałych wierzchołków tego trapezu.
jest osią symetrii tego trapezu. Wyznacz współrzędne pozostałych wierzchołków tego trapezu.
Wyznacz wszystkie wartości parametru 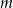 , dla których prosta o równaniu
, dla których prosta o równaniu 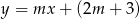 ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie
ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie 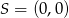 i promieniu
i promieniu 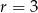 .
.
Punkty 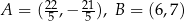 oraz
oraz 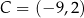 są wierzchołkami trójkąta
są wierzchołkami trójkąta 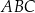 . Symetralna boku
. Symetralna boku 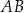 tego trójkąta przecina bok
tego trójkąta przecina bok 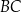 w punkcie
w punkcie 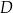 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 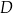 .
.
Odległość każdego z wierzchołków 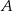 i
i 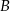 trójkąta
trójkąta 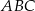 od punktu
od punktu 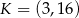 jest równa
jest równa 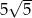 , a odległość tych wierzchołków od punktu
, a odległość tych wierzchołków od punktu 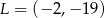 jest równa 25. Okrąg opisany na trójkącie
jest równa 25. Okrąg opisany na trójkącie 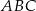 jest styczny do prostej
jest styczny do prostej 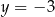 w punkcie
w punkcie 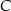 . Punkt
. Punkt 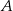 znajduje się w pierwszej ćwiartce układu współrzędnych. Wyznacz współrzędne wierzchołków trójkąta
znajduje się w pierwszej ćwiartce układu współrzędnych. Wyznacz współrzędne wierzchołków trójkąta 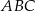 .
.
Dana jest prosta 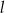 o równaniu
o równaniu 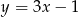 oraz punkt
oraz punkt 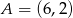 . Wyznacz punkt
. Wyznacz punkt 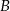 symetryczny do punktu
symetryczny do punktu 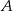 względem prostej
względem prostej 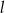 .
.
Wyznacz współrzędne punktu 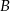 , który jest symetryczny do punktu
, który jest symetryczny do punktu 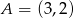 względem prostej
względem prostej 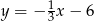 .
.
Dany jest kwadrat 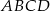 o polu 10 i wierzchołku
o polu 10 i wierzchołku 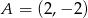 . Przekątna
. Przekątna 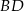 tego kwadratu ma równanie
tego kwadratu ma równanie 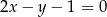 . Oblicz współrzędne pozostałych wierzchołków kwadratu.
. Oblicz współrzędne pozostałych wierzchołków kwadratu.
Prosta 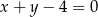 przecina oś
przecina oś 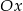 w punkcie
w punkcie 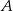 i oś
i oś 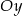 w punkcie
w punkcie 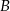 . Punkt
. Punkt 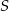 jest środkiem odcinka
jest środkiem odcinka 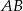 . Znajdź równanie okręgu o środku w punkcie
. Znajdź równanie okręgu o środku w punkcie 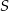 i promieniu
i promieniu 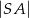 .
.

