W prostokącie 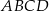 dane są
dane są 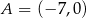 ,
, 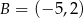 i
i 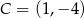 . Napisz równanie prostej, która jest styczna w punkcie
. Napisz równanie prostej, która jest styczna w punkcie 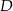 do okręgu opisanego na prostokącie
do okręgu opisanego na prostokącie 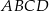 .
.
/Szkoła średnia/Geometria/Geometria analityczna
Punkt 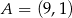 jest wierzchołkiem rombu
jest wierzchołkiem rombu 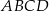 o polu 60. Przekątna
o polu 60. Przekątna 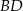 zawiera się w prostej
zawiera się w prostej 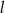 o równaniu
o równaniu 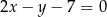 . Wyznacz równanie okręgu wpisanego w ten romb.
. Wyznacz równanie okręgu wpisanego w ten romb.
Określ wzajemne położenie prostych 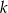 i
i 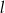 o równaniach
o równaniach
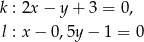
Punkt 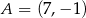 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 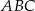 , w którym
, w którym 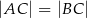 . Obie współrzędne wierzchołka
. Obie współrzędne wierzchołka 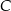 są liczbami ujemnymi. Okrąg wpisany w trójkąt
są liczbami ujemnymi. Okrąg wpisany w trójkąt 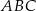 ma równanie
ma równanie 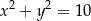 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 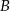 i
i 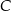 tego trójkąta.
tego trójkąta.
Punkt 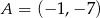 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 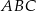 , w którym
, w którym 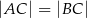 . Obie współrzędne wierzchołka
. Obie współrzędne wierzchołka 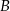 są liczbami dodatnimi. Okrąg wpisany w trójkąt
są liczbami dodatnimi. Okrąg wpisany w trójkąt 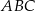 ma równanie
ma równanie 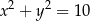 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 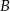 i
i 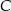 tego trójkąta.
tego trójkąta.
Dany jest odcinek 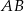 , w którym środek ma współrzędne
, w którym środek ma współrzędne 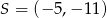 , a koniec
, a koniec 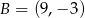 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 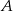 .
.
Dany jest jeden koniec odcinka 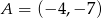 i jego środek
i jego środek 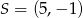 . Wyznacz współrzędne drugiego końca tego odcinka.
. Wyznacz współrzędne drugiego końca tego odcinka.
Oblicz miarę kąta ostrego, którego ramiona są zawarte w prostych o równaniach 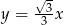 i
i 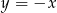 .
.
Oblicz miarę kąta ostrego, którego ramiona są zawarte w prostych o równaniach 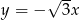 i
i 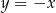 .
.
Punkt 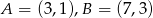 są kolejnymi wierzchołkami kwadratu
są kolejnymi wierzchołkami kwadratu 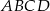 . Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.
. Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.
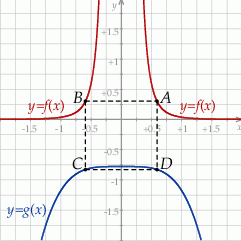
Rozpatrujemy wszystkie prostokąty 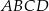 , których wierzchołki
, których wierzchołki 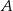 i
i 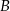 leżą na wykresie funkcji
leżą na wykresie funkcji 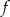 określonej wzorem
określonej wzorem 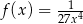 dla
dla 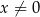 . Punkty
. Punkty 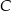 i
i 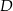 leżą na wykresie funkcji
leżą na wykresie funkcji 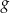 określonej wzorem
określonej wzorem 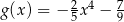 i są położone symetrycznie względem osi
i są położone symetrycznie względem osi 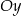 (zobacz rysunek). Oblicz współrzędne wierzchołka
(zobacz rysunek). Oblicz współrzędne wierzchołka 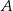 , dla którego pole prostokąta
, dla którego pole prostokąta 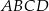 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.
Punkty 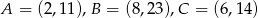 są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka 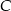 przecina prostą
przecina prostą 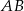 w punkcie
w punkcie 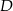 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 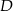 .
.
Punkty 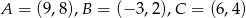 są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka 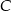 przecina prostą
przecina prostą 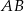 w punkcie
w punkcie 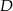 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 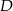 .
.
W kartezjańskim układzie współrzędnych 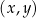 przekątne równoległoboku
przekątne równoległoboku 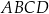 przecinają się w punkcie
przecinają się w punkcie 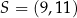 . Bok
. Bok 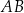 tego równoległoboku zawiera się w prostej o równaniu
tego równoległoboku zawiera się w prostej o równaniu 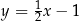 , a bok
, a bok 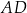 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 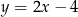 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 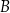 .
.
W kartezjańskim układzie współrzędnych 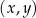 przekątne równoległoboku
przekątne równoległoboku 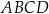 przecinają się w punkcie
przecinają się w punkcie 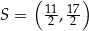 . Bok
. Bok 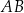 tego równoległoboku zawiera się w prostej o równaniu
tego równoległoboku zawiera się w prostej o równaniu 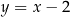 , a bok
, a bok 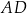 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 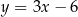 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 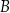 .
.
W rombie 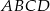 dane są
dane są 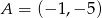 i punkt przecięcia przekątnych
i punkt przecięcia przekątnych 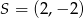 . Wierzchołek
. Wierzchołek 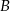 leży na prostej
leży na prostej 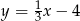 . Oblicz współrzędne pozostałych wierzchołków rombu.
. Oblicz współrzędne pozostałych wierzchołków rombu.
Oblicz współrzędne punktów przecięcia wykresów funkcji 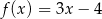 i funkcji
i funkcji 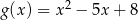 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 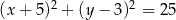 równoległych do prostej o równaniu
równoległych do prostej o równaniu 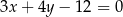 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 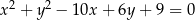 równoległych do prostej o równaniu
równoległych do prostej o równaniu 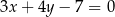 .
.
Punkt 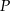 jest punktem wspólnym przekątnych trapezu
jest punktem wspólnym przekątnych trapezu 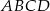 , w którym
, w którym 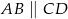 oraz
oraz ![−→ −→ −→ D = (1 0,− 9),AB = [12,21],CB = [0,13],CP = [− 3,− 2]](https://img.zadania.info/zad/6347587/HzadT3x.gif) . Oblicz współrzędne pozostałych wierzchołków trapezu
. Oblicz współrzędne pozostałych wierzchołków trapezu 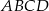 .
.
W układzie współrzędnych są dane punkty 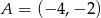 ,
, 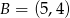 .
.
- Oblicz odległość punktu
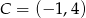 od prostej przechodzącej przez punkty
od prostej przechodzącej przez punkty 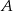 i
i 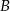 .
. - Uzasadnij, że jeśli
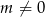 , to punkty
, to punkty 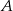 ,
, 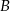 oraz punkt
oraz punkt 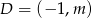 są wierzchołkami trójkąta.
są wierzchołkami trójkąta.
Jeden z końców odcinka leży na paraboli 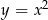 , a drugi na prostej o równaniu
, a drugi na prostej o równaniu 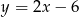 . Wykaż, że długość tego odcinka jest nie mniejsza od
. Wykaż, że długość tego odcinka jest nie mniejsza od 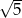 . Sporządź odpowiedni rysunek.
. Sporządź odpowiedni rysunek.
Trójkąt o wierzchołkach 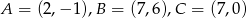 przekształcono w jednokładności o skali
przekształcono w jednokładności o skali 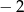 i otrzymano trójkąt o wierzchołkach
i otrzymano trójkąt o wierzchołkach  . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 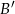 i
i 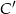 jeżeli
jeżeli 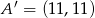 .
.
Oblicz promień okręgu opisanego na trójkącie o wierzchołkach 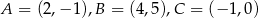 .
.
Jaką figurę na płaszczyźnie określa podane równanie parametryczne:
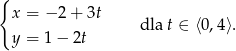
Jaką figurę na płaszczyźnie określa podane równanie parametryczne:
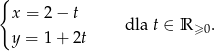
Punkty 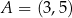 ,
, 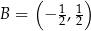 ,
, 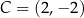 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 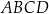 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 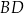 tego równoległoboku.
tego równoległoboku.

