Wyznacz równanie prostej przechodzącej przez punkty 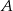 i
i 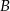 jeżeli
jeżeli 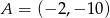 i
i 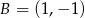 .
.
/Szkoła średnia/Geometria/Geometria analityczna
Wyznacz równanie prostej przechodzącej przez punkty 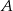 i
i 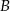 jeżeli
jeżeli 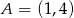 i
i 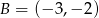 .
.
Zapisz równanie ogólne i kierunkowe prostej 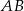 , jeśli
, jeśli 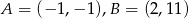 .
.
Zapisz równanie ogólne i kierunkowe prostej 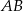 , jeśli
, jeśli 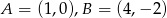 .
.
Zapisz równanie ogólne i kierunkowe prostej 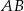 , jeśli
, jeśli 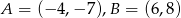 .
.
Punkt 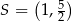 leży wewnątrz figury
leży wewnątrz figury 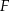 opisanej układem nierówności
opisanej układem nierówności
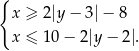
Wyznacz równanie największego okręgu o środku 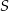 , który jest zawarty wewnątrz figury
, który jest zawarty wewnątrz figury 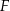 .
.
Wierzchołki czworokąta 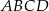 mają współrzędne:
mają współrzędne: 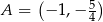 ,
, 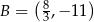 ,
, 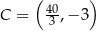 i
i  .
.
- Wykaż, że czworokąt
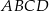 jest trapezem równoramiennym, w który można wpisać okrąg.
jest trapezem równoramiennym, w który można wpisać okrąg. - Wyznacz współrzędne punktu styczności okręgu wpisanego w czworokąt
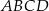 z prostą
z prostą 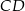 .
.
Trapez równoramienny 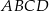 o podstawach
o podstawach 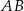 i
i 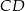 jest opisany na okręgu o równaniu
jest opisany na okręgu o równaniu 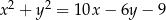 . Okrąg ten przecina boki
. Okrąg ten przecina boki 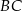 i
i 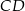 tego trapezu odpowiednio w punktach
tego trapezu odpowiednio w punktach 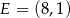 i
i 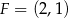 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 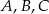 i
i 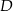 tego trapezu.
tego trapezu.
Podstawa 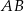 trójkąta równoramiennego
trójkąta równoramiennego 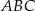 zawarta jest w prostej
zawarta jest w prostej 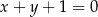 . Ramię
. Ramię 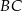 zawiera się w prostej
zawiera się w prostej 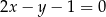 . Wyznacz równanie prostej
. Wyznacz równanie prostej 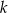 , zawierającej ramię
, zawierającej ramię 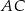 , wiedząc że punkt
, wiedząc że punkt 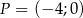 należy do prostej
należy do prostej 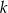 .
.
Punkty 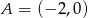 i
i 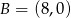 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 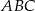 o przeciwprostokątnej
o przeciwprostokątnej 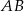 i polu równym 15. Oblicz współrzędne punktu
i polu równym 15. Oblicz współrzędne punktu 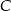 .
.
Na hiperboli 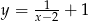 wyznacz taki punkt
wyznacz taki punkt 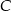 , który jest równoodległy od punktów
, który jest równoodległy od punktów 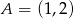 i
i 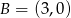 .
.
W trójkącie 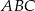 dane są
dane są 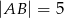 ,
, 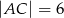 oraz iloczyn skalarny
oraz iloczyn skalarny 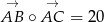 . Oblicz miarę kąta
. Oblicz miarę kąta 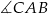 oraz pole tego trójkąta.
oraz pole tego trójkąta.
Prosta 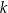 o równaniu
o równaniu 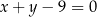 przecina parabolę o równaniu
przecina parabolę o równaniu 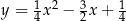 w punktach
w punktach 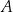 oraz
oraz 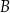 . Pierwsza współrzędna punktu
. Pierwsza współrzędna punktu 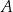 jest liczbą dodatnią; pierwsza współrzędna punktu
jest liczbą dodatnią; pierwsza współrzędna punktu 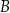 jest liczbą ujemną. Prosta
jest liczbą ujemną. Prosta 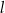 jest równoległa do prostej
jest równoległa do prostej 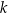 i styczna do danej paraboli w punkcie
i styczna do danej paraboli w punkcie 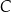 . Oblicz odległość punktu
. Oblicz odległość punktu 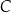 od prostej
od prostej 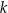 oraz pole trójkąta
oraz pole trójkąta 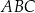 .
.
Prosta 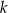 o równaniu
o równaniu 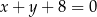 przecina parabolę o równaniu
przecina parabolę o równaniu 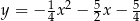 w punktach
w punktach 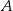 oraz
oraz 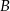 . Pierwsza współrzędna punktu
. Pierwsza współrzędna punktu 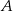 jest liczbą ujemną; pierwsza współrzędna punktu
jest liczbą ujemną; pierwsza współrzędna punktu 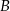 jest liczbą dodatnią. Prosta
jest liczbą dodatnią. Prosta 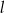 jest równoległa do prostej
jest równoległa do prostej 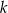 i styczna do danej paraboli w punkcie
i styczna do danej paraboli w punkcie 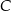 . Oblicz odległość punktu
. Oblicz odległość punktu 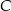 od prostej
od prostej 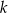 oraz pole trójkąta
oraz pole trójkąta 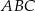 .
.
Punkty 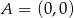 ,
, 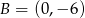 i
i 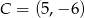 są wierzchołkami trapezu prostokątnego o polu 36 i podstawach
są wierzchołkami trapezu prostokątnego o polu 36 i podstawach 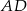 i
i 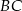 . Oblicz pole trójkąta
. Oblicz pole trójkąta 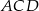 .
.
Za pomocą rachunku wektorowego pokazać, że środki boków dowolnego czworokąta tworzą wierzchołki równoległoboku.
W okrąg o równaniu 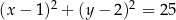 wpisano trójkąt
wpisano trójkąt 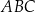 . Bok
. Bok 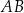 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu 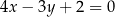 . Wysokość
. Wysokość 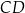 tego trójkąta dzieli bok
tego trójkąta dzieli bok 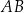 tak, że
tak, że 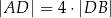 . Oblicz pole trójkąta
. Oblicz pole trójkąta 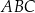 .
.
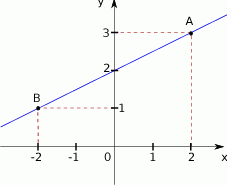
Na płaszczyźnie dane są punkty 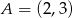 i
i 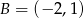 (patrz rysunek). Zbadaj, czy punkty
(patrz rysunek). Zbadaj, czy punkty 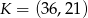 i
i 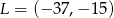 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 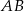 . Podaj odpowiedź i jej uzasadnienie.
. Podaj odpowiedź i jej uzasadnienie.
Punkt 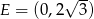 jest środkiem boku
jest środkiem boku 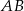 trójkąta równobocznego
trójkąta równobocznego 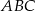 , prosta
, prosta 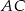 ma równanie
ma równanie 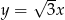 , a początek układu współrzędnych pokrywa się wierzchołkiem
, a początek układu współrzędnych pokrywa się wierzchołkiem 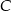 tego trójkąta. Napisz równania wysokości trójkąta
tego trójkąta. Napisz równania wysokości trójkąta 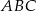 przechodzących przez wierzchołki
przechodzących przez wierzchołki 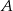 i
i 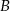 .
.
Początkowe ramię kąta  pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt
pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt 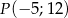 . Oblicz wartość wyrażenia:
. Oblicz wartość wyrażenia: 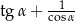 .
.
Początkowe ramię kąta  pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt
pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt 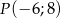 . Oblicz wartość wyrażenia:
. Oblicz wartość wyrażenia: 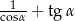 .
.
Wyznacz równanie zbioru środków wszystkich okręgów stycznych zewnętrznie do okręgu 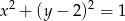 i stycznych do prostej
i stycznych do prostej 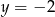 .
.
Czworokąt 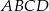 ma środek symetrii. Znajdź współrzędne punktu
ma środek symetrii. Znajdź współrzędne punktu 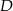 jeżeli:
jeżeli: 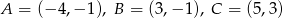 .
.
Czworokąt 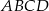 ma środek symetrii. Znajdź współrzędne punktu
ma środek symetrii. Znajdź współrzędne punktu 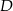 jeżeli:
jeżeli: 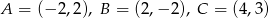 .
.
Punkt 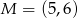 jest środkiem ramienia
jest środkiem ramienia 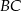 trójkąta równoramiennego
trójkąta równoramiennego 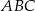 , w którym
, w którym 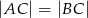 . Podstawa
. Podstawa  tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 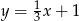 oraz
oraz 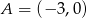 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 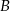 tego trójkąta.
tego trójkąta.
Wyznacz równanie okręgu o środku 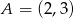 , stycznego do prostej o równaniu
, stycznego do prostej o równaniu 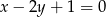 .
.
Wyznacz równanie okręgu o środku 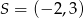 stycznego do prostej
stycznego do prostej 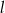 o równaniu
o równaniu 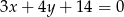 .
.
Wyznacz równanie okręgu o środku 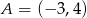 , stycznego do prostej o równaniu
, stycznego do prostej o równaniu 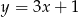 .
.
W trójkącie 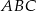 dane są
dane są 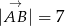 ,
, 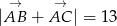 oraz
oraz 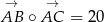 . Oblicz długość boku
. Oblicz długość boku 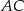 , oraz miarę kąta
, oraz miarę kąta 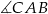 .
.

