Punkty 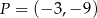 ,
, 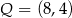 i
i 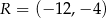 są środkami odpowiednio boków
są środkami odpowiednio boków 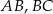 i
i 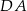 równoległoboku
równoległoboku 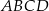 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 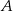 tego równoległoboku.
tego równoległoboku.
/Szkoła średnia/Geometria/Geometria analityczna
Punkt 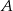 jest punktem wspólnym prostych prostopadłych
jest punktem wspólnym prostych prostopadłych 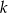 i
i 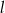 o równaniach
o równaniach 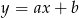 oraz
oraz 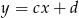 . Wykaż, że jeżeli
. Wykaż, że jeżeli 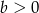 i
i 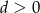 , to druga współrzędna punktu
, to druga współrzędna punktu 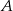 jest liczbą dodatnią.
jest liczbą dodatnią.
Wierzchołek kąta znajduje się w punkcie 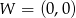 , jedno z jego ramion leży na prostej
, jedno z jego ramion leży na prostej 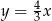 , a drugie ramię przechodzi przez punkt
, a drugie ramię przechodzi przez punkt 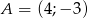 . Punkt
. Punkt 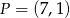 należy do wnętrza tego kąta. Sprawdź rachunkowo, czy punkt
należy do wnętrza tego kąta. Sprawdź rachunkowo, czy punkt 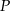 leży na dwusiecznej tego kąta.
leży na dwusiecznej tego kąta.
Punkty 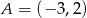 i
i 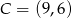 są przeciwległymi wierzchołkami rombu o polu 40. Wyznacz współrzędne pozostałych wierzchołków rombu.
są przeciwległymi wierzchołkami rombu o polu 40. Wyznacz współrzędne pozostałych wierzchołków rombu.
W rombie 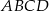 , którego pole jest równe 10 dane są przeciwległe wierzchołki
, którego pole jest równe 10 dane są przeciwległe wierzchołki 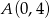 i
i 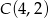 . Wyznacz współrzędne pozostałych wierzchołków rombu.
. Wyznacz współrzędne pozostałych wierzchołków rombu.
Punkty 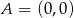 i
i 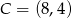 są wierzchołkami rombu
są wierzchołkami rombu 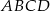 , którego jeden z boków zawiera się w prostej
, którego jeden z boków zawiera się w prostej 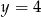 . Wyznacz współrzędne pozostałych wierzchołków rombu.
. Wyznacz współrzędne pozostałych wierzchołków rombu.
Wyznacz odległość między prostymi 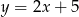 i
i 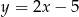 .
.
Dane są punkty 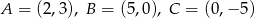 .
.
- Uzasadnij, że proste
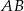 i
i 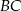 są prostopadłe.
są prostopadłe. - Wyznacz współrzędne takiego punktu
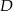 , dla którego czworokąt
, dla którego czworokąt 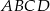 jest prostokątem.
jest prostokątem. - Oblicz pole prostokąta
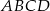 .
.
Dany jest trójkąt 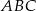 , gdzie
, gdzie 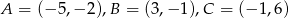 .
.
- Wyznacz równanie prostej zawierającej bok
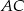 .
. - Oblicz długość środkowej
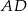 .
. - Wyznacz równanie prostej zawierającej wysokość poprowadzoną z wierzchołka
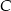 .
. - Oblicz pole tego trójkąta.
Dany jest trójkąt 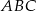 , gdzie
, gdzie 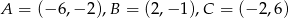 .
.
- Wyznacz równanie prostej zawierającej bok
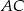 .
. - Oblicz długość środkowej
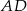 .
. - Wyznacz równanie prostej zawierającej wysokość poprowadzoną z wierzchołka
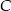 .
. - Oblicz pole tego trójkąta.
Przedłużenia ramion 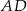 i
i 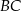 trapezu równoramiennego
trapezu równoramiennego 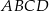 przecinają się w punkcie
przecinają się w punkcie 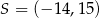 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 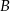 i
i 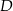 tego trapezu, jeżeli
tego trapezu, jeżeli 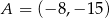 i
i 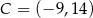 .
.
Dwa boki trójkąta prostokątnego 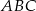 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 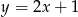 oraz
oraz 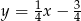 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 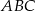 jeżeli wiadomo, że jego trzeci bok jest zawarty w prostej przechodzącej przez punkt
jeżeli wiadomo, że jego trzeci bok jest zawarty w prostej przechodzącej przez punkt 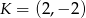 . Rozważ wszystkie możliwości.
. Rozważ wszystkie możliwości.
Napisz równanie okręgu przechodzącego przez punkt 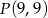 i stycznego do osi
i stycznego do osi  w punkcie
w punkcie 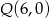 .
.
Punkt 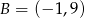 należy do okręgu stycznego do osi
należy do okręgu stycznego do osi 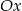 w punkcie
w punkcie 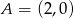 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu.
Napisz równanie okręgu przechodzącego przez punkt 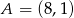 i stycznego do osi
i stycznego do osi 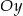 w punkcie
w punkcie 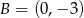 .
.
Do okręgu należy punkt 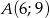 , oraz jest on styczny do osi
, oraz jest on styczny do osi 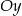 w punkcie
w punkcie 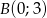 . Podaj równanie tego okręgu.
. Podaj równanie tego okręgu.
Do okręgu należy punkt 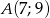 , oraz jest on styczny do osi
, oraz jest on styczny do osi 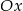 w punkcie
w punkcie 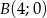 . Podaj równanie tego okręgu.
. Podaj równanie tego okręgu.
Sprawdź czy punkt 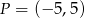 jest środkiem okręgu wpisanego w trójkąt o wierzchołkach
jest środkiem okręgu wpisanego w trójkąt o wierzchołkach 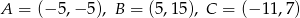 .
.
Na okręgu o równaniu 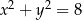 opisano romb o polu
opisano romb o polu 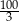 . Dłuższa przekątna rombu zawiera się w prostej o równaniu
. Dłuższa przekątna rombu zawiera się w prostej o równaniu 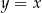 . Oblicz współrzędne wierzchołków tego rombu.
. Oblicz współrzędne wierzchołków tego rombu.
Podstawa trójkąta równoramiennego zawiera się w prostej 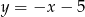 , a jedno z jego ramion w prostej
, a jedno z jego ramion w prostej 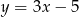 . Wyznacz równanie drugiego ramienia tego trójkąta, jeżeli jednym z jego wierzchołków jest punkt o współrzędnych
. Wyznacz równanie drugiego ramienia tego trójkąta, jeżeli jednym z jego wierzchołków jest punkt o współrzędnych 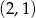 .
.
Znajdź taki punkt 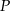 leżący na prostej
leżący na prostej 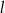 o równaniu
o równaniu 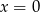 , z którego odcinek
, z którego odcinek 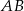 , gdzie
, gdzie 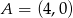 ,
, 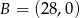 , widać pod możliwie największym kątem. Wyznacz ten kąt.
, widać pod możliwie największym kątem. Wyznacz ten kąt.
Punkty 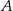 i
i 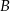 są punktami wspólnymi prostej o równaniu
są punktami wspólnymi prostej o równaniu 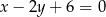 oraz okręgu o środku
oraz okręgu o środku 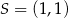 . Długość odcinka
. Długość odcinka 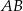 jest równa
jest równa 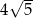 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 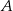 i
i 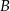 .
.
Prosta o równaniu 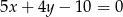 przecina oś
przecina oś 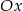 układu współrzędnych w punkcie
układu współrzędnych w punkcie 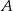 oraz oś
oraz oś 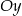 w punkcie
w punkcie 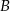 . Oblicz współrzędne wszystkich punktów
. Oblicz współrzędne wszystkich punktów 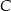 leżących na osi
leżących na osi 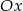 i takich, że trójkąt
i takich, że trójkąt 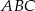 ma pole równe 35 .
ma pole równe 35 .
Mając dane współrzędne punktu 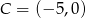 kwadratu
kwadratu 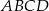 oraz współrzędne punktu przecięcia się przekątnych
oraz współrzędne punktu przecięcia się przekątnych 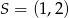 , wyznacz współrzędne pozostałych wierzchołków kwadratu
, wyznacz współrzędne pozostałych wierzchołków kwadratu 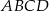 .
.
Na bokach 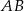 i
i 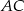 trójkąta
trójkąta 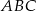 wybrano punkty
wybrano punkty 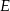 i
i 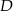 w ten sposób, że
w ten sposób, że 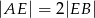 i
i 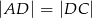 . Punkt
. Punkt 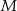 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 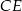 i
i 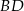 .
.
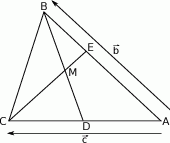
- Przedstaw każdy z wektorów
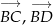 oraz
oraz 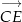 w postaci
w postaci 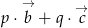 , gdzie
, gdzie 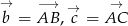 oraz
oraz 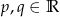 .
. - Korzystając z równości
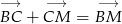 oblicz w jakim stosunku punkt
oblicz w jakim stosunku punkt 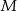 dzieli odcinki
dzieli odcinki 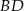 i
i 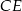 .
.
Wyznacz równanie prostej przechodzącej przez punkty 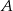 i
i 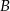 jeżeli
jeżeli 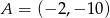 i
i 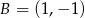 .
.
Wyznacz równanie prostej przechodzącej przez punkty 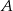 i
i 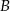 jeżeli
jeżeli 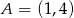 i
i 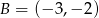 .
.

