Napisz równanie prostopadłej opuszczonej z wierzchołka 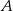 trójkąta
trójkąta 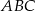 o wierzchołkach
o wierzchołkach 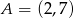 ,
, 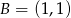 i
i 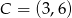 na środkową
na środkową 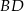 boku
boku 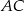 .
.
/Szkoła średnia/Geometria/Geometria analityczna
Oblicz odległość środka okręgu 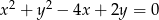 od prostej
od prostej 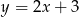 .
.
Dany jest czworokąt 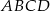 , gdzie
, gdzie 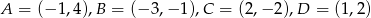 .
.
- Oblicz pole czworokąta
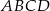 .
. - Oblicz wartość wyrażenia
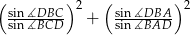 .
.
Wyznacz wartość parametru 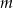 , dla której odległość punktu
, dla której odległość punktu 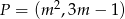 od prostej
od prostej 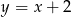 jest najmniejsza możliwa.
jest najmniejsza możliwa.
Wyznacz współrzędne środka okręgu, który jest obrazem okręgu o równaniu 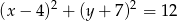 w jednokładności o środku
w jednokładności o środku 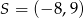 i skali
i skali 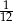 .
.
Boki 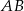 i
i 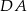 równoległoboku
równoległoboku 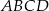 są zawarte odpowiednio w prostych o równaniach
są zawarte odpowiednio w prostych o równaniach 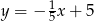 i
i 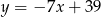 . Napisz równanie prostej zawierającej przekątną
. Napisz równanie prostej zawierającej przekątną 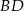 tego równoległoboku, jeżeli jego środek ma współrzędne
tego równoległoboku, jeżeli jego środek ma współrzędne 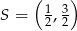 .
.
Rozważamy trójkąty 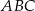 , w których
, w których 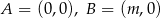 , gdzie
, gdzie 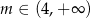 , a wierzchołek
, a wierzchołek 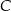 leży na prostej o równaniu
leży na prostej o równaniu 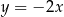 . Na boku
. Na boku 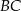 tego trójkąta leży punkt
tego trójkąta leży punkt 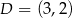 .
.
- Wykaż, że dla
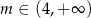 pole
pole 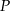 trójkąta
trójkąta 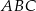 , jako funkcja zmiennej
, jako funkcja zmiennej 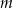 , wyraża się wzorem
, wyraża się wzorem 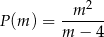
- Oblicz tę wartość
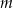 , dla której funkcja
, dla której funkcja 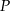 osiąga wartość najmniejszą. Wyznacz równanie prostej
osiąga wartość najmniejszą. Wyznacz równanie prostej 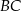 , przy której funkcja
, przy której funkcja 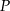 osiąga tę najmniejszą wartość.
osiąga tę najmniejszą wartość.
Napisz równanie prostej równoległej do prostej o równaniu 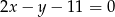 i przechodzącej przez punkt
i przechodzącej przez punkt 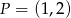 .
.
Na przedziale ![[− 1,7]](https://img.zadania.info/zad/5154135/HzadT0x.gif) określono dwie funkcje:
określono dwie funkcje: 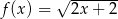 i
i 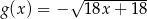 . Rozpatrujemy wszystkie trapezy
. Rozpatrujemy wszystkie trapezy 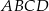 , których wierzchołki
, których wierzchołki 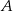 i
i 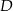 leżą na wykresie funkcji
leżą na wykresie funkcji 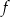 , a wierzchołki
, a wierzchołki 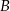 i
i 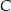 leżą na wykresie funkcji
leżą na wykresie funkcji 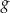 . Podstawy rozpatrywanych trapezów są równoległe do osi
. Podstawy rozpatrywanych trapezów są równoległe do osi 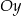 (zobacz rysunek).
(zobacz rysunek).
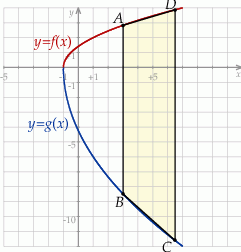
Oblicz współrzędne wierzchołków tego z rozpatrywanych trapezów, w którym 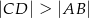 , i który ma największe możliwe pole. Oblicz to największe pole. Przy rozwiązywaniu zadania możesz skorzystać z tego, że jeżeli pierwsza współrzędna wierzchołka
, i który ma największe możliwe pole. Oblicz to największe pole. Przy rozwiązywaniu zadania możesz skorzystać z tego, że jeżeli pierwsza współrzędna wierzchołka 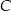 trapezu
trapezu 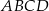 jest równa 7, a druga współrzędna wierzchołka
jest równa 7, a druga współrzędna wierzchołka 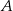 jest równa
jest równa 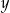 , to pole trapezu wyraża się wzorem
, to pole trapezu wyraża się wzorem
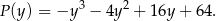
Wyznacz odległość między prostymi
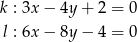
Dane są dwa okręgi o równaniach 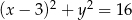 i
i 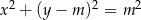 ,
, 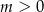 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 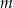 , dla których te okręgi mają jeden punkt wspólny.
, dla których te okręgi mają jeden punkt wspólny.
Dane są dwa okręgi o równaniach 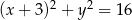 i
i 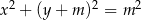 ,
, 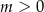 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 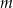 , dla których te okręgi mają jeden punkt wspólny.
, dla których te okręgi mają jeden punkt wspólny.
Bok 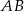 kwadratu
kwadratu 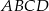 o polu równym 4 jest zawarty w prostej o równaniu
o polu równym 4 jest zawarty w prostej o równaniu 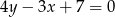 . Wiadomo ponadto, że wewnątrz tego kwadratu leży początek układu współrzędnych. Napisz równanie prostej zawierającej bok
. Wiadomo ponadto, że wewnątrz tego kwadratu leży początek układu współrzędnych. Napisz równanie prostej zawierającej bok 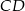 tego kwadratu.
tego kwadratu.
Wyznacz współrzędne punktów wspólnych prostej 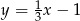 i okręgu
i okręgu 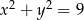 .
.
Wyznacz punkty wspólne okręgu 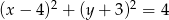 oraz prostej
oraz prostej 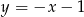 .
.
Oblicz pole i obwód rombu 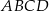 wiedząc, że przekątna
wiedząc, że przekątna 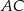 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 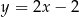 oraz
oraz 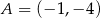 i
i 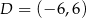 .
.
Napisz równanie okręgu, którego środek znajduje się na prostej 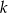 , przechodzącego przez punkty
, przechodzącego przez punkty 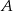 i
i 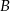 , jeśli
, jeśli 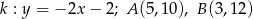 .
.
Napisz równanie okręgu, którego środek znajduje się na prostej 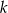 , przechodzącego przez punkty
, przechodzącego przez punkty 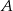 i
i 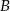 , jeśli
, jeśli 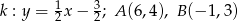 .
.
Okrąg przechodzi przez punkty 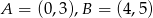 , a jego środek należy do prostej o równaniu
, a jego środek należy do prostej o równaniu 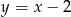 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu.
W trójkącie prostokątnym 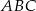 o przeciwprostokątnej
o przeciwprostokątnej 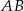 dane są wierzchołki
dane są wierzchołki 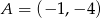 i
i 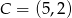 . Punkt
. Punkt 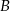 leży na prostej o równaniu
leży na prostej o równaniu 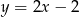 . Wyznacz równanie okręgu opisanego na tym trójkącie.
. Wyznacz równanie okręgu opisanego na tym trójkącie.
Wyznacz współrzędne wierzchołków trójkąta, którego boki zawarte są w prostych o równaniach 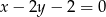 ,
, 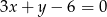 ,
, 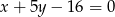 .
.
Oblicz długość cięciwy, którą wycina z prostej 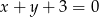 okrąg o środku w punkcie
okrąg o środku w punkcie 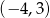 i promieniu 10.
i promieniu 10.
Oblicz długość cięciwy, którą wycina z prostej 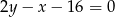 okrąg o środku w punkcie
okrąg o środku w punkcie 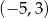 i promieniu 5.
i promieniu 5.
Wyznacz odległość punktu 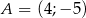 od miejsca zerowego funkcji
od miejsca zerowego funkcji 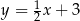 .
.
Wyznacz odległość punktu 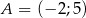 od miejsca zerowego funkcji
od miejsca zerowego funkcji 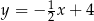 .
.
Przez początek układu współrzędnych poprowadzono prostą przecinającą okrąg 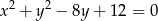 w dwóch punktach
w dwóch punktach 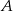 i
i 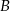 . Uzasadnij, że liczba
. Uzasadnij, że liczba  nie zależy od wyboru prostej i oblicz wartość tego iloczynu.
nie zależy od wyboru prostej i oblicz wartość tego iloczynu.

