Wyznacz współrzędne środka ciężkości trójkąta w zależności od współrzędnych jego wierzchołków.
/Szkoła średnia/Geometria/Geometria analityczna
Na rysunku poniżej przedstawiono fragment wykresu funkcji 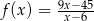 określonej dla
określonej dla 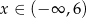 . Wykres ten przecina osie
. Wykres ten przecina osie 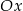 i
i 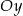 odpowiednio w punktach
odpowiednio w punktach 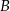 i
i 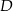 , a punkt
, a punkt 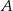 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 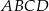 , w których punkt
, w których punkt 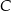 leży na wykresie funkcji
leży na wykresie funkcji 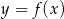 pomiędzy punktami
pomiędzy punktami 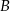 i
i 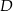 .
.
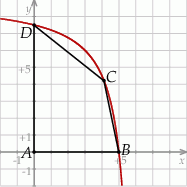
Oblicz współrzędne wierzchołka 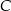 tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe.
W układzie współrzędnych rozważmy wszystkie punkty 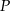 postaci:
postaci: 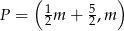 , gdzie
, gdzie 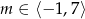 . Oblicz najmniejszą i największą wartość
. Oblicz najmniejszą i największą wartość 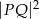 , gdzie
, gdzie 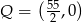 .
.
Wyznacz równanie okręgu, który jest obrazem okręgu 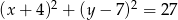 w jednokładności o środku
w jednokładności o środku 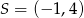 i skali
i skali 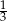 .
.
Wyznacz równanie okręgu, który jest obrazem okręgu 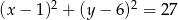 w jednokładności o środku
w jednokładności o środku 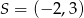 i skali
i skali 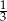 .
.
Przekątna 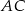 czworokąta
czworokąta 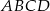 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 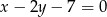 . Wierzchołki
. Wierzchołki 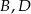 tego czworokąta mają współrzędne
tego czworokąta mają współrzędne 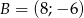 ,
, 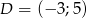 . Oblicz współrzędne punktu przecięcia się przekątnych czworokąta
. Oblicz współrzędne punktu przecięcia się przekątnych czworokąta 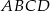 .
.
Punkt 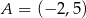 jest jednym z wierzchołków trójkąta równoramiennego
jest jednym z wierzchołków trójkąta równoramiennego 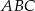 , w którym
, w którym 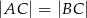 . Pole tego trójkąta jest równe 15. Bok
. Pole tego trójkąta jest równe 15. Bok 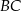 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 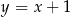 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 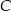 .
.
Wierzchołki 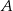 i
i 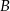 trójkąta prostokątnego
trójkąta prostokątnego 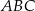 leżą na osi
leżą na osi 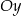 układu współrzędnych. Okrąg wpisany w ten trójkąt jest styczny do boków
układu współrzędnych. Okrąg wpisany w ten trójkąt jest styczny do boków 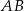 ,
, 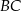 i
i 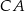 w punktach – odpowiednio –
w punktach – odpowiednio – 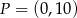 ,
, 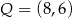 i
i 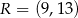 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 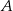 ,
, 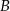 i
i 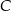 tego trójkąta.
tego trójkąta.
Wierzchołki 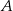 i
i 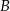 trójkąta prostokątnego
trójkąta prostokątnego 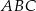 leżą na prostej
leżą na prostej 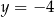 . Okrąg wpisany w ten trójkąt jest styczny do boków
. Okrąg wpisany w ten trójkąt jest styczny do boków 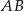 ,
, 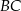 i
i 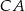 odpowiednio w punktach
odpowiednio w punktach 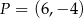 ,
, 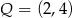 i
i 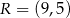 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 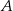 ,
, 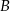 i
i 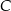 tego trójkąta.
tego trójkąta.
Okrąg o środku w punkcie 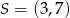 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 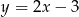 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Okrąg o środku w punkcie 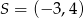 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 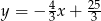 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Okrąg o środku w punkcie 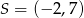 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 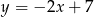 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Okrąg o środku w punkcie 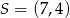 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 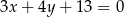 . Oblicz promień tego okręgu oraz współrzędne punktu styczności.
. Oblicz promień tego okręgu oraz współrzędne punktu styczności.
Oblicz, ile jest punktów 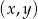 na płaszczyźnie, których współrzędne
na płaszczyźnie, których współrzędne  i
i 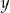 są liczbami całkowitymi spełniającymi odpowiednio nierówności:
są liczbami całkowitymi spełniającymi odpowiednio nierówności: 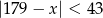 i
i 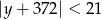 .
.
Narysuj w układzie współrzędnych zbiór
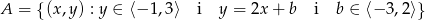
oraz oblicz jego pole powierzchni.
Napisz równanie okręgu, który jest styczny do prostej 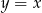 w punkcie
w punkcie 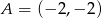 , oraz który odcina z prostej
, oraz który odcina z prostej 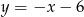 cięciwę o długości 8.
cięciwę o długości 8.
Wykaż, że punkt o współrzędnych 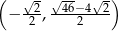 jest wierzchołkiem kwadratu opisanego na okręgu o równaniu
jest wierzchołkiem kwadratu opisanego na okręgu o równaniu
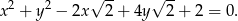
Zapisz równanie okręgu o środku 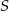 i promieniu
i promieniu  , jeśli
, jeśli 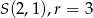 .
.
Zapisz równanie okręgu o środku 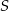 i promieniu
i promieniu  , jeśli
, jeśli 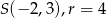 .
.
W układzie współrzędnych na płaszczyźnie dane są punkty: 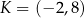 i
i 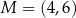 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 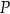 takiego, że jeden z trzech punktów
takiego, że jeden z trzech punktów 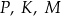 jest środkiem odcinka o końcach w dwóch pozostałych punktach. Zapisz wszystkie możliwości.
jest środkiem odcinka o końcach w dwóch pozostałych punktach. Zapisz wszystkie możliwości.
Dane są wektory ![→ a = [1,− 2]](https://img.zadania.info/zad/8690556/HzadT0x.gif) ,
, ![→ b = [− 2,− 1]](https://img.zadania.info/zad/8690556/HzadT1x.gif) ,
, ![→ c = [3,4]](https://img.zadania.info/zad/8690556/HzadT2x.gif) . Dobierz wartości parametrów
. Dobierz wartości parametrów 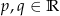 tak, aby wektory
tak, aby wektory 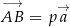 ,
, 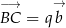 i
i 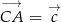 tworzyły trójkąt
tworzyły trójkąt 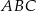 .
.
Punkty 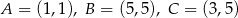 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 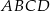 niebędącego równoległobokiem, w którym
niebędącego równoległobokiem, w którym 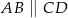 .
.
- Wyznacz równanie osi symetrii tego trapezu.
- Oblicz pole tego trapezu.
W trójkącie prostokątnym 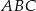 , gdzie
, gdzie 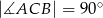 , wierzchołek
, wierzchołek 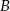 ma współrzędne
ma współrzędne 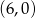 . Prosta
. Prosta 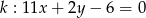 , zawierająca środkową trójkąta poprowadzoną z wierzchołka
, zawierająca środkową trójkąta poprowadzoną z wierzchołka 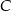 , przecina bok
, przecina bok 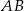 trójkąta w punkcie
trójkąta w punkcie 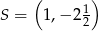 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 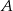 i
i 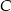 .
.
Punkty 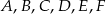 są kolejnymi wierzchołkami sześciokąta foremnego, przy czym
są kolejnymi wierzchołkami sześciokąta foremnego, przy czym 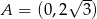 ,
, 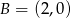 , a
, a 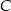 leży na osi
leży na osi 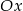 . Wyznacz równanie stycznej do okręgu opisanego na tym sześciokącie przechodzącej przez wierzchołek
. Wyznacz równanie stycznej do okręgu opisanego na tym sześciokącie przechodzącej przez wierzchołek 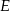 .
.
Dany jest okrąg o równaniu 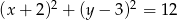 oraz punkt
oraz punkt 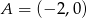 . Napisz równanie symetralnej odcinka, którego końcami są dany punkt
. Napisz równanie symetralnej odcinka, którego końcami są dany punkt 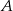 i środek
i środek 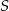 danego okręgu.
danego okręgu.
Odcinek 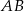 o długości 4 jest zawarty w prostej o równaniu
o długości 4 jest zawarty w prostej o równaniu 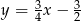 . Symetralna odcinka
. Symetralna odcinka 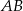 przecina oś
przecina oś 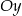 w punkcie
w punkcie 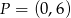 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 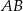 .
.
Odcinek 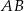 o długości 20 jest zawarty w prostej o równaniu
o długości 20 jest zawarty w prostej o równaniu 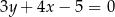 . Symetralna odcinka
. Symetralna odcinka 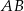 przecina oś
przecina oś 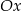 w punkcie
w punkcie 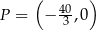 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 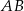 .
.

