W trójkącie równoramiennym 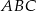 o podstawie
o podstawie 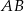 poprowadzono wysokość z wierzchołka
poprowadzono wysokość z wierzchołka 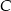 . Wyznacz równanie prostej zawierającej tę wysokość, jeśli
. Wyznacz równanie prostej zawierającej tę wysokość, jeśli 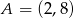 ,
, 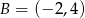 .
.
/Szkoła średnia/Geometria/Geometria analityczna
Z punktu 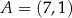 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 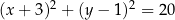 . Oblicz pole trójkąta
. Oblicz pole trójkąta 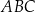 , gdzie
, gdzie 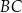 jest odcinkiem łączącym punkty styczności.
jest odcinkiem łączącym punkty styczności.
Z punktu 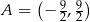 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 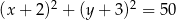 . Oblicz pole trójkąta
. Oblicz pole trójkąta 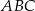 , gdzie
, gdzie 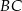 jest odcinkiem łączącym punkty styczności.
jest odcinkiem łączącym punkty styczności.
Przekątne kwadratu 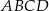 przecinają się w punkcie
przecinają się w punkcie 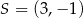 , a jeden z jego boków jest zawarty w prostej
, a jeden z jego boków jest zawarty w prostej 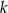 o równaniu
o równaniu 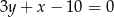 . Wyznacz współrzędne wierzchołków kwadratu
. Wyznacz współrzędne wierzchołków kwadratu 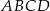 .
.
Na krzywej 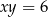 obrano punkty
obrano punkty 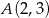 i
i 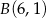 . Znajdź na tej krzywej taki punkt
. Znajdź na tej krzywej taki punkt 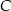 o ujemnej odciętej, aby pole trójkąta
o ujemnej odciętej, aby pole trójkąta 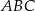 było najmniejsze.
było najmniejsze.
Wyznacz wszystkie wartości parametru 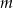 , dla których okrąg o równaniu
, dla których okrąg o równaniu 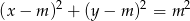 jest styczny do prostej
jest styczny do prostej 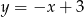 .
.
Punkty 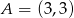 i
i 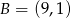 są wierzchołkami trójkąta
są wierzchołkami trójkąta 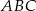 , a punkt
, a punkt 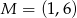 jest środkiem boku
jest środkiem boku 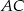 . Oblicz współrzędne punktu przecięcia prostej
. Oblicz współrzędne punktu przecięcia prostej 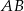 z wysokością tego trójkąta, poprowadzoną z wierzchołka
z wysokością tego trójkąta, poprowadzoną z wierzchołka 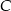 .
.
Dane są równania prostych 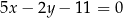 i
i 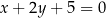 , w których zawierają się dwa boki równoległoboku. Punkt
, w których zawierają się dwa boki równoległoboku. Punkt 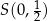 jest środkiem symetrii tego równoległoboku. Znajdź równania prostych, w których zawierają się pozostałe boki równoległoboku.
jest środkiem symetrii tego równoległoboku. Znajdź równania prostych, w których zawierają się pozostałe boki równoległoboku.
Dane są punkty 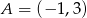 i
i 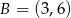 . Funkcja
. Funkcja 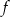 przyporządkowuje dowolnemu punktowi należącemu do odcinka
przyporządkowuje dowolnemu punktowi należącemu do odcinka 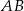 jego odległość od punktu
jego odległość od punktu 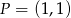 . Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.
. Wyznacz zbiór wartości tej funkcji i jej wartość najmniejszą.
Z punktu 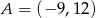 poprowadzono styczne do okręgu o równaniu
poprowadzono styczne do okręgu o równaniu 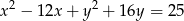 . Oblicz długość odcinka łączącego punkty styczności.
. Oblicz długość odcinka łączącego punkty styczności.
Z punktu 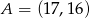 poprowadzono styczne do okręgu o równaniu
poprowadzono styczne do okręgu o równaniu 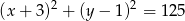 . Oblicz długość odcinka łączącego punkty styczności.
. Oblicz długość odcinka łączącego punkty styczności.
Odcinek 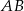 jest wysokością trójkąta równobocznego. Oblicz długość boku trójkąta, jeśli wiadomo, że
jest wysokością trójkąta równobocznego. Oblicz długość boku trójkąta, jeśli wiadomo, że 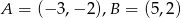
Rozpatrujemy wszystkie trójkąty 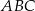 , których wierzchołki
, których wierzchołki 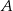 i
i 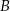 leżą na wykresie funkcji
leżą na wykresie funkcji 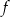 określonej wzorem
określonej wzorem 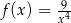 dla
dla 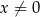 . Punkt
. Punkt 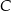 ma współrzędne
ma współrzędne 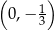 , a punkty
, a punkty 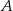 i
i 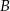 , są położone symetrycznie względem osi
, są położone symetrycznie względem osi 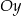 (zobacz rysunek). Oblicz współrzędne wierzchołków
(zobacz rysunek). Oblicz współrzędne wierzchołków 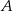 i
i 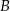 , dla których pole trójkąta
, dla których pole trójkąta 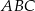 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.
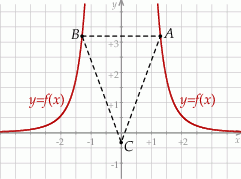
Wyznacz równanie symetralnej przeciwprostokątnej trójkąta prostokątnego o wierzchołkach 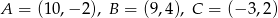 .
.
W układzie współrzędnych punkty 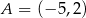 i
i 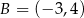 są końcami cięciwy okręgu
są końcami cięciwy okręgu  . Średnica
. Średnica 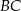 tego okręgu jest zwarta w prostej o równaniu
tego okręgu jest zwarta w prostej o równaniu 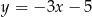 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 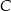 .
.
Wyznacz współrzędne punktu przecięcia przekątnych czworokąta 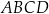 jeżeli
jeżeli 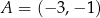 ,
, 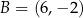 ,
, 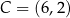 i
i 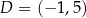 .
.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 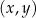 , punkty
, punkty 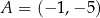 ,
, 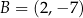 ,
, 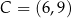 i
i 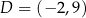 są wierzchołkami czworokąta
są wierzchołkami czworokąta 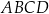 . Oblicz współrzędne punktu przecięcia przekątnych czworokąta
. Oblicz współrzędne punktu przecięcia przekątnych czworokąta 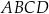 .
.
Wyznacz współrzędne punktu przecięcia przekątnych czworokąta 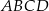 jeżeli
jeżeli 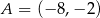 ,
, 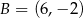 ,
, 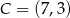 i
i 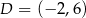 .
.
Wyznacz równanie okręgu o promieniu  , który przechodzi przez punkty wspólne okręgów o równaniach
, który przechodzi przez punkty wspólne okręgów o równaniach 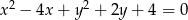 i
i 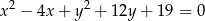 .
.
Napisz równanie okręgu opisanego na trapezie równoramiennym 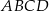 , jeżeli
, jeżeli 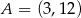 ,
, 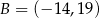 ,
, 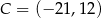 i
i 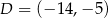 .
.
Na rysunku przedstawiono położenie miejscowości 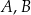 i
i 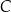 oraz zaznaczono odległości między nimi. O godzinie 9:00 z miejscowości
oraz zaznaczono odległości między nimi. O godzinie 9:00 z miejscowości 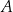 do
do 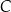 wyruszył zastęp harcerzy Tropiciele i przemieszczał się z prędkością 4 km/h. O tej samej godzinie z miejscowości
wyruszył zastęp harcerzy Tropiciele i przemieszczał się z prędkością 4 km/h. O tej samej godzinie z miejscowości 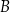 do
do 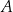 wyruszył zastęp harcerzy Korsarze i przemieszczał się z prędkością 2 km/h.
wyruszył zastęp harcerzy Korsarze i przemieszczał się z prędkością 2 km/h.
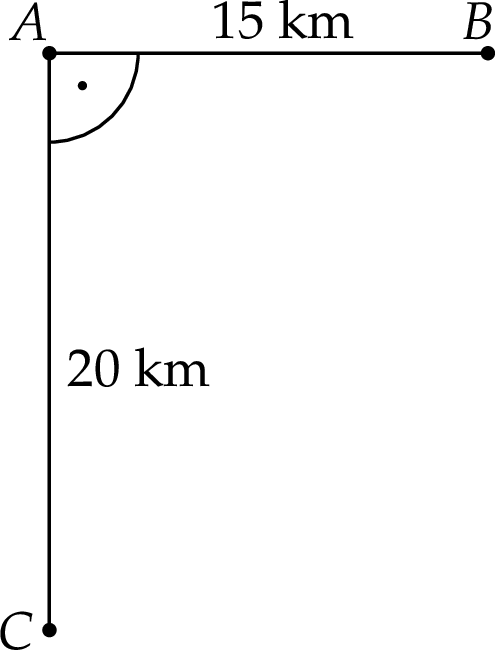
Wyznacz godzinę, o której odległość między tymi zastępami harcerzy będzie najmniejsza. Przyjmij, że mierzymy odległość między zastępami do momentu, w którym zastęp Tropicieli dotrze do miejscowości 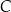 .
.
Sprawdź, czy odległość środka okręgu 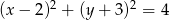 od prostej
od prostej 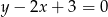 jest równa promieniowi okręgu.
jest równa promieniowi okręgu.
Dane są dwa wierzchołki trójkąta 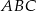 :
: 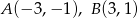 . Punkt
. Punkt 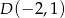 należy do boku
należy do boku 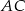 , a odcinek
, a odcinek 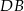 jest środkową w trójkącie
jest środkową w trójkącie 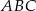 . Oblicz:
. Oblicz:
- współrzędne wierzchołka
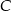 ;
; - pole trójkąta
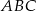 .
.
Wykres funkcji kwadratowej 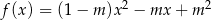 przecina oś
przecina oś 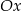 w punktach
w punktach 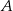 i
i 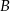 , które leżą po dwóch różnych stronach osi
, które leżą po dwóch różnych stronach osi 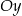 . Wyznacz tę wartość parametru
. Wyznacz tę wartość parametru 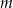 , dla której iloczyn odległości punktów
, dla której iloczyn odległości punktów 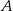 i
i 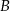 od początku układu współrzędnych jest najmniejszy możliwy. Dla wyznaczonej wartości
od początku układu współrzędnych jest najmniejszy możliwy. Dla wyznaczonej wartości 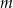 oblicz sumę odległości punktów
oblicz sumę odległości punktów 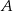 i
i  od początku układu współrzędnych.
od początku układu współrzędnych.

