W układzie współrzędnych na płaszczyźnie zaznaczono punkty 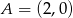 i
i 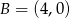 . Wyznacz wszystkie możliwe położenia punktu
. Wyznacz wszystkie możliwe położenia punktu 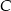 , dla których
, dla których 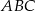 jest trójkątem równoramiennym o podstawie
jest trójkątem równoramiennym o podstawie 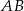 i polu równym 3.
i polu równym 3.
/Szkoła średnia/Geometria/Geometria analityczna
Dwa boki kwadratu zawierają się w prostych o równaniach 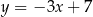 i
i 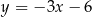 . Oblicz pole tego kwadratu.
. Oblicz pole tego kwadratu.
W kartezjańskim układzie współrzędnych 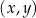 przekątne równoległoboku
przekątne równoległoboku 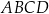 przecinają się w punkcie
przecinają się w punkcie 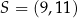 . Bok
. Bok 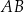 tego równoległoboku zawiera się w prostej o równaniu
tego równoległoboku zawiera się w prostej o równaniu 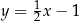 , a bok
, a bok 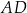 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 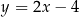 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 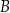 oraz długość odcinka
oraz długość odcinka 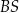 .
.
Znajdź równanie prostej 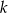 przechodzącej przez punkt
przechodzącej przez punkt 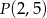 , która ogranicza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu równym 36.
, która ogranicza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu równym 36.
Prosta o równaniu 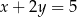 zawiera przekątną
zawiera przekątną 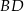 rombu
rombu 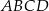 , którego bok ma długość 5. Wyznacz współrzędne wierzchołków rombu jeżeli
, którego bok ma długość 5. Wyznacz współrzędne wierzchołków rombu jeżeli 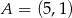 .
.
Okrąg o równaniu 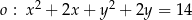 jest styczny do prostych
jest styczny do prostych 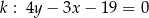 i
i 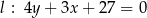 w punktach
w punktach 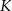 i
i 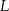 odpowiednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu
odpowiednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu  , prostych
, prostych 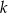 i
i 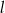 , oraz nie przechodzą przez punkty
, oraz nie przechodzą przez punkty 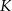 i
i 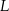 .
.
Napisz równanie okręgu opisanego na trójkącie o wierzchołkach 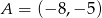 ,
, 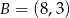 i
i 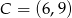 .
.
W prostokącie 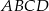 dany jest wierzchołek
dany jest wierzchołek 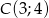 oraz
oraz ![−→ AB = [4;3]](https://img.zadania.info/zad/4338487/HzadT2x.gif) . Znajdź równania przekątnych wiedząc, że wierzchołek
. Znajdź równania przekątnych wiedząc, że wierzchołek 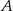 należy do prostej
należy do prostej 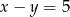 .
.
Prosta 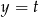 przecina proste
przecina proste 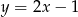 i
i 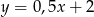 odpowiednio w punktach
odpowiednio w punktach 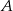 i
i 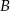 .
.
- Wyraź długość odcinka
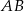 jako funkcję zmiennej
jako funkcję zmiennej 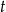 .
. - Wyznacz takie punkty
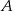 i
i 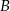 , aby długość odcinka
, aby długość odcinka 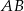 była równa 3.
była równa 3.
Prosta 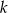 jest wykresem funkcji
jest wykresem funkcji 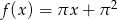 .
.
- Oblicz współrzędne punktu przecięcia prostej
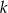 z wykresem funkcji
z wykresem funkcji 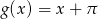 .
. - Znajdź równanie prostej przechodzącej przez punkt
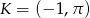 i równoległej do prostej
i równoległej do prostej 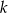 .
.
Określ wzajemne położenie okręgów: 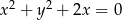 i
i 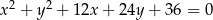 .
.
Odcinek o końcach 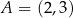 i
i 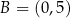 jest podstawą trapezu
jest podstawą trapezu 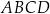 . Druga podstawa o środku w punkcie
. Druga podstawa o środku w punkcie 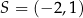 jest dwa razy dłuższa od podstawy
jest dwa razy dłuższa od podstawy 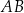 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 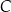 i
i 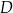 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Na paraboli o równaniu 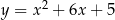 znajdź współrzędne punktu
znajdź współrzędne punktu 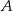 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 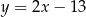 jest najmniejsza.
jest najmniejsza.
Na paraboli o równaniu 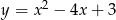 wyznacz punkt, którego odległość od prostej
wyznacz punkt, którego odległość od prostej 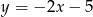 jest najmniejsza.
jest najmniejsza.
Dane są parabola o równaniu 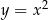 oraz punkty
oraz punkty 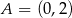 i
i 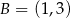 (zobacz rysunek).
(zobacz rysunek).
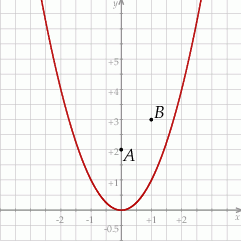
Rozpatrujemy wszystkie trójkąty 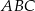 , których wierzchołek
, których wierzchołek 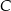 leży na tej paraboli. Niech
leży na tej paraboli. Niech 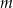 oznacza pierwszą współrzędną punktu
oznacza pierwszą współrzędną punktu 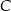 .
.
- Wyznacz pole
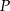 trójkąta
trójkąta 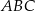 jako funkcję zmiennej
jako funkcję zmiennej 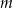 .
. - Wyznacz wszystkie wartości
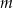 , dla których trójkąt
, dla których trójkąt 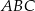 jest ostrokątny.
jest ostrokątny.
Dane są parabola o równaniu 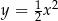 oraz punkty
oraz punkty 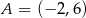 i
i 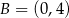 (zobacz rysunek).
(zobacz rysunek).
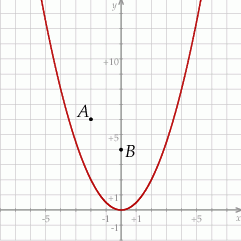
Rozpatrujemy wszystkie trójkąty 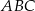 , których wierzchołek
, których wierzchołek 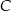 leży na tej paraboli. Niech
leży na tej paraboli. Niech 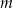 oznacza pierwszą współrzędną punktu
oznacza pierwszą współrzędną punktu 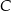 .
.
- Wyznacz pole
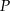 trójkąta
trójkąta 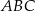 jako funkcję zmiennej
jako funkcję zmiennej 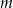 .
. - Wyznacz wszystkie wartości
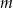 , dla których trójkąt
, dla których trójkąt 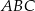 jest ostrokątny.
jest ostrokątny.
Punkty 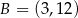 ,
, 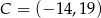 i
i 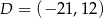 są kolejnymi wierzchołkami trapezu równoramiennego
są kolejnymi wierzchołkami trapezu równoramiennego 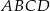 , który nie jest równoległobokiem, i w którym
, który nie jest równoległobokiem, i w którym 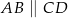 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 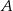 tego trapezu.
tego trapezu.
W kwadracie 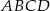 dane są wierzchołek
dane są wierzchołek 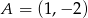 i środek symetrii
i środek symetrii 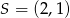 . Oblicz pole kwadratu
. Oblicz pole kwadratu 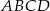 .
.
Dane są punkty 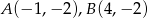 oraz
oraz 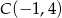 .
.
- Za pomocą odpowiedniego układu nierówności opisz trójkąt
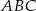 .
. - Oblicz odległość punktu
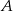 od prostej
od prostej 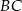 .
. - Oblicz promień koła wpisanego w trójkąt
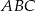 .
. - Wyznacz równanie symetralnej boku
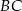 .
.
Punkty 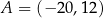 i
i 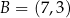 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 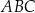 , w którym
, w którym 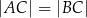 . Wierzchołek
. Wierzchołek 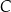 leży na osi
leży na osi 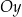 układu współrzędnych. Oblicz współrzędne wierzchołka
układu współrzędnych. Oblicz współrzędne wierzchołka 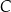 oraz obwód tego trójkąta.
oraz obwód tego trójkąta.
Punkty 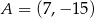 i
i 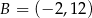 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 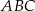 , w którym
, w którym 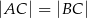 . Wierzchołek
. Wierzchołek 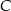 leży na prostej
leży na prostej 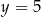 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 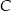 oraz obwód tego trójkąta.
oraz obwód tego trójkąta.
W kartezjańskim układzie współrzędnych 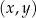 punkty
punkty 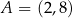 oraz
oraz 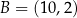 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 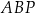 , w którym
, w którym 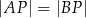 . Wierzchołek
. Wierzchołek 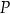 leży na osi
leży na osi 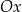 układu współrzędnych. Oblicz współrzędne punktu
układu współrzędnych. Oblicz współrzędne punktu 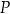 oraz długość odcinka
oraz długość odcinka 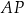 .
.
Końce cięciwy 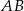 okręgu o równaniu
okręgu o równaniu 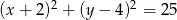 leżą na prostej
leżą na prostej 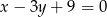 . Oblicz sinus kąta wypukłego
. Oblicz sinus kąta wypukłego 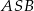 , gdzie
, gdzie 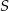 jest środkiem danego okręgu.
jest środkiem danego okręgu.
Punkty 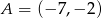 i
i 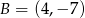 są wierzchołkami podstawy trójkąta równoramiennego
są wierzchołkami podstawy trójkąta równoramiennego 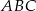 , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka 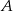 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 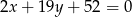 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 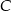 .
.
Punkty 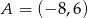 i
i 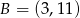 są wierzchołkami podstawy trójkąta równoramiennego
są wierzchołkami podstawy trójkąta równoramiennego 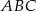 , a wysokość opuszczona z wierzchołka
, a wysokość opuszczona z wierzchołka 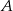 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 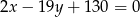 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 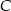 .
.

