Dana jest parabola opisana równaniem 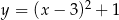 . Tworzymy trójkąty
. Tworzymy trójkąty 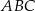 takie, że punkt
takie, że punkt 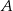 leży w początku układu współrzędnych, punkt
leży w początku układu współrzędnych, punkt 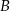 o współrzędnych
o współrzędnych 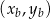 leży na paraboli, punkt
leży na paraboli, punkt 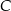 ma współrzędne
ma współrzędne 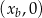 .
.
- Napisz wzór funkcji
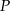 , określającej pole trójkąta
, określającej pole trójkąta 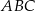 w zależności od
w zależności od 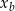 dla
dla 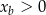 .
. - Znajdź trójkąt o największym polu dla
![xb ∈ [0;2]](https://img.zadania.info/zad/3724416/HzadT11x.gif) ; w odpowiedzi podaj współrzędne punktu
; w odpowiedzi podaj współrzędne punktu 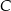 .
.

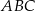 o wierzchołkach
o wierzchołkach 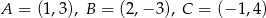 w jednokładności o środku
w jednokładności o środku 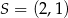 i skali
i skali 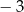 jest trójkąt
jest trójkąt 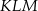 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 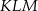 .
. 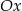 pod kątem
pod kątem 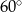 , a oś
, a oś 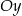 w punkcie
w punkcie 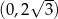 .
. 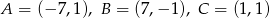 opuszczonej z wierzchołka
opuszczonej z wierzchołka 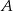 .
. 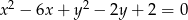 i prosta
i prosta 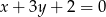 przecinają się w punktach
przecinają się w punktach 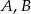 . Wyznacz długość cięciwy
. Wyznacz długość cięciwy 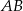 tego okręgu.
tego okręgu. 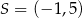 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 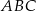 , w którym
, w którym 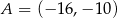 i
i 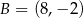 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 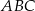 .
. 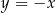 wyznacz punkt, który jest równo odległy od początku układu współrzędnych oraz od punktu
wyznacz punkt, który jest równo odległy od początku układu współrzędnych oraz od punktu 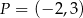 .
. 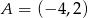 i
i 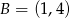 oraz prosta
oraz prosta 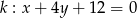 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 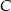 leżącego na prostej
leżącego na prostej 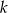 i tak samo odległego od punktów
i tak samo odległego od punktów 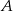 i
i 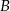 .
. 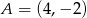 i
i 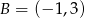 oraz prosta
oraz prosta 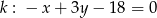 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 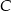 leżącego na prostej
leżącego na prostej 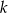 i tak samo odległego od punktów
i tak samo odległego od punktów 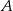 i
i 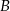 .
. 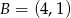 i
i 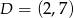 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 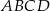 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 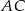 tego rombu.
tego rombu. 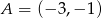 i
i 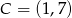 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 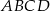 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 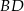 tego rombu.
tego rombu. 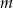 wykres funkcji
wykres funkcji 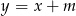 ma co najmniej jeden punkt wspólny z okręgiem o promieniu
ma co najmniej jeden punkt wspólny z okręgiem o promieniu  , którego środkiem jest początek układu współrzędnych?
, którego środkiem jest początek układu współrzędnych? 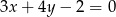 i
i 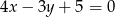 .
. 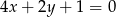 i
i 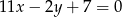 .
. 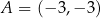 ,
, 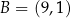 i
i 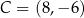 . Wyznacz wszystkie punkty
. Wyznacz wszystkie punkty 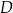 prostej
prostej 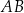 , które są różne od punktów
, które są różne od punktów 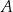 i
i 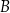 , i dla których suma pól trójkątów
, i dla których suma pól trójkątów 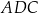 i
i 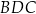 jest mniejsza od 120.
jest mniejsza od 120. 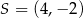 przechodzi przez punkt
przechodzi przez punkt 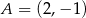 . Napisz równanie stycznej do tego okręgu przechodzącej przez punkt
. Napisz równanie stycznej do tego okręgu przechodzącej przez punkt 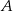 .
. 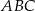 w jednokładności o środku
w jednokładności o środku 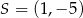 i skali
i skali 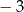 jest trójkąt
jest trójkąt 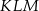 o wierzchołkach
o wierzchołkach 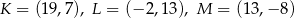 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 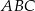 .
. 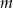 proste
proste 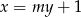 oraz
oraz 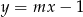 przecinają się w jednym punkcie, który leży poniżej prostej
przecinają się w jednym punkcie, który leży poniżej prostej 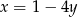 ?
? 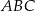 , w którym
, w którym 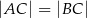 oraz
oraz 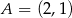 i
i 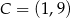 . Podstawa
. Podstawa 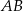 tego trójkąta jest zawarta w prostej
tego trójkąta jest zawarta w prostej 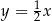 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 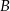 .
. 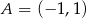 i
i 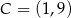 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 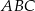 , w którym
, w którym 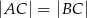 . Podstawa
. Podstawa 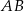 tego trójkąta zawiera się w prostej o równaniu
tego trójkąta zawiera się w prostej o równaniu 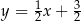 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 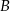 tego trójkąta.
tego trójkąta. 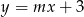 tworzy z dodatnimi półosiami układu współrzędnych trójkąt o polu 7. Wyznacz
tworzy z dodatnimi półosiami układu współrzędnych trójkąt o polu 7. Wyznacz 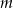 .
.  są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 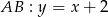 ,
, 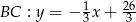 i
i 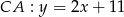 . Wyznacz współrzędne środka okręgu opisanego na trójkącie
. Wyznacz współrzędne środka okręgu opisanego na trójkącie 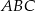 .
. 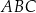 , w którym
, w którym 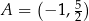 . Bok
. Bok 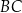 tego trójkąta jest zwarty w prostej o równaniu
tego trójkąta jest zwarty w prostej o równaniu 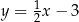 . Oblicz współrzędne środka odcinka
. Oblicz współrzędne środka odcinka 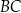 oraz oblicz pole trójkąta
oraz oblicz pole trójkąta 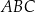 .
. 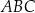 , w którym
, w którym 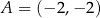 oraz
oraz 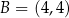 , kąt przy wierzchołku
, kąt przy wierzchołku 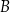 jest rozwarty. Bok
jest rozwarty. Bok 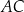 zawiera się w prostej
zawiera się w prostej 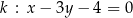 . Środek okręgu opisanego na trójkącie
. Środek okręgu opisanego na trójkącie 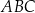 znajduje się w odległości
znajduje się w odległości 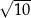 od boku
od boku 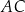 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu. 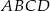 (
(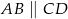 i
i 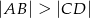 ) leżą na paraboli o równaniu
) leżą na paraboli o równaniu 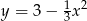 . Wierzchołki
. Wierzchołki 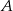 i
i 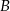 są punktami przecięcia tej paraboli z osią
są punktami przecięcia tej paraboli z osią 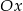 . Oblicz współrzędne wierzchołka trapezu o obu współrzędnych dodatnich, dla którego pole trapezu jest równe
. Oblicz współrzędne wierzchołka trapezu o obu współrzędnych dodatnich, dla którego pole trapezu jest równe 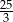 .
. 