Okrąg 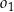 o równaniu
o równaniu 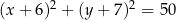 oraz okrąg
oraz okrąg 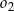 o środku
o środku 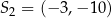 są wewnętrznie styczne, przy czym okrąg
są wewnętrznie styczne, przy czym okrąg 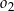 zawiera się w kole opisanym nierównością
zawiera się w kole opisanym nierównością 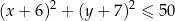 . Napisz równanie wspólnej stycznej do obu okręgów.
. Napisz równanie wspólnej stycznej do obu okręgów.
/Szkoła średnia/Geometria/Geometria analityczna
W czworokącie 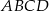 przekątne przecinają się w punkcie o współrzędnych
przekątne przecinają się w punkcie o współrzędnych 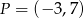 w taki sposób, że
w taki sposób, że 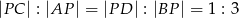 . Wiedząc, że
. Wiedząc, że ![− → AC = [4,6]](https://img.zadania.info/zad/3335440/HzadT3x.gif) i
i ![−→ BD = [− 10,− 2]](https://img.zadania.info/zad/3335440/HzadT4x.gif) , oblicz współrzędne wierzchołków tego czworokąta. Uzasadnij, że czworokąt
, oblicz współrzędne wierzchołków tego czworokąta. Uzasadnij, że czworokąt 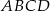 jest trapezem.
jest trapezem.
W prostokącie 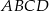 dane są wierzchołek
dane są wierzchołek 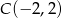 i wektor
i wektor ![→ AB = [3 ,3]](https://img.zadania.info/zad/3365079/HzadT2x.gif) . Wyznacz równania prostych, zawierających przekątne tego prostokąta, jeśli wiadomo, że wierzchołek
. Wyznacz równania prostych, zawierających przekątne tego prostokąta, jeśli wiadomo, że wierzchołek 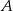 należy do prostej o równaniu
należy do prostej o równaniu 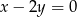 .
.
Odcinek 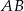 , gdzie
, gdzie 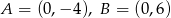 , jest przeciwprostokątną trójkąta prostokątnego
, jest przeciwprostokątną trójkąta prostokątnego 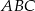 . Wierzchołek
. Wierzchołek 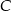 o ujemnej odciętej należy do prostej
o ujemnej odciętej należy do prostej 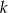 o równaniu
o równaniu 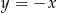 .
.
- Oblicz współrzędne wierzchołka
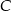 .
. - Obrazem trójkąta
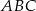 w jednokładności o środku
w jednokładności o środku 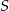 i skali
i skali 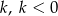 , jest trójkąt
, jest trójkąt 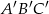 , którego pole wynosi 5. Wiedząc dodatkowo, że
, którego pole wynosi 5. Wiedząc dodatkowo, że 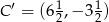 , oblicz skalę jednokładności i współrzędne punktu
, oblicz skalę jednokładności i współrzędne punktu 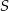 .
.
Oblicz odległość punktu 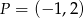 od prostej o równaniu
od prostej o równaniu 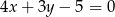 .
.
Napisz równanie okręgu o środku w punkcie 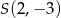 , stycznego do osi
, stycznego do osi 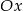 .
.
Środek okręgu, stycznego do osi 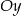 i do prostej o równaniu
i do prostej o równaniu 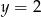 , ma obie współrzędne ujemne. Promień okręgu ma długość 5. Wyznacz równanie tego okręgu.
, ma obie współrzędne ujemne. Promień okręgu ma długość 5. Wyznacz równanie tego okręgu.
Napisz równanie okręgu o promieniu 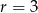 , stycznego do obu osi układu.
, stycznego do obu osi układu.
Styczne do okręgu o równaniu 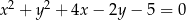 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 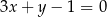 , przecinają prostą
, przecinają prostą 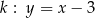 w punktach
w punktach 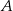 i
i 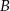 . Oblicz pole trójkąta
. Oblicz pole trójkąta 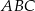 , jeśli
, jeśli 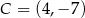 .
.
Znając współrzędne wierzchołków trójkąta 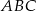 ,
, 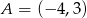 ,
, 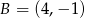 oraz punkt przecięcia się jego wysokości
oraz punkt przecięcia się jego wysokości 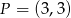 wyznacz współrzędne wierzchołka
wyznacz współrzędne wierzchołka 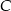 .
.
Jeden bok kwadratu opisanego okręgu o równaniu 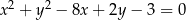 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 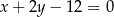 . Oblicz współrzędne wierzchołków tego kwadratu.
. Oblicz współrzędne wierzchołków tego kwadratu.
Prosta o równaniu 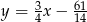 jest styczna od okręgu o środku
jest styczna od okręgu o środku 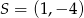 . Wyznacz promień tego okręgu.
. Wyznacz promień tego okręgu.
Prosta o równaniu 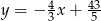 jest styczna od okręgu o środku
jest styczna od okręgu o środku 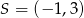 . Wyznacz promień tego okręgu.
. Wyznacz promień tego okręgu.
Wierzchołek 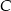 trójkąta
trójkąta 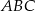 leży na okręgu o równaniu
leży na okręgu o równaniu 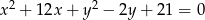 , a pozostałe wierzchołki mają współrzędne
, a pozostałe wierzchołki mają współrzędne 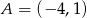 i
i 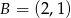 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
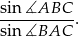
Proste 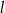 i
i 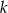 przecinają się w punkcie
przecinają się w punkcie 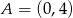 . Prosta
. Prosta 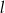 wyznacza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu 8, zaś prosta
wyznacza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu 8, zaś prosta 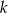 – trójkąt o polu 10. Oblicz pole trójkąta, którego wierzchołkami są: punkt
– trójkąt o polu 10. Oblicz pole trójkąta, którego wierzchołkami są: punkt 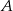 oraz punkty przecięcia prostych
oraz punkty przecięcia prostych 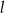 i
i 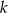 z osią
z osią 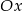 .
.
Punkt 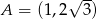 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 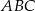 . Bok
. Bok 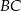 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 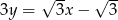 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 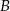 i
i 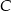 trójkąta.
trójkąta.
W układzie współrzędnych na płaszczyźnie punkty 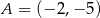 i
i 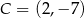 są przeciwległymi wierzchołkami deltoidu
są przeciwległymi wierzchołkami deltoidu 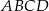 , w którym
, w którym 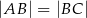 . Wyznacz równanie prostej
. Wyznacz równanie prostej 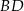 .
.
W układzie współrzędnych na płaszczyźnie punkty 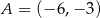 i
i 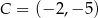 są przeciwległymi wierzchołkami deltoidu
są przeciwległymi wierzchołkami deltoidu 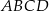 , w którym
, w którym 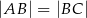 . Wyznacz równanie prostej
. Wyznacz równanie prostej 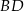 .
.
Dana jest prosta 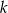 o równaniu
o równaniu 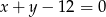 oraz punkt
oraz punkt 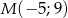 wyznacz na prostej
wyznacz na prostej 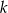 takie punkty
takie punkty 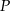 i
i 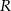 aby
aby 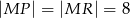 .
.
Dany jest punkt 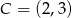 i prosta o równaniu
i prosta o równaniu 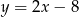 będąca symetralną odcinka
będąca symetralną odcinka 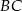 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 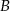 . Wykonaj obliczenia uzasadniające odpowiedź.
. Wykonaj obliczenia uzasadniające odpowiedź.
Punkt 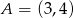 jest wierzchołkiem kąta prostego w równoramiennym trójkącie prostokątnym
jest wierzchołkiem kąta prostego w równoramiennym trójkącie prostokątnym 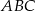 . Przeciwprostokątna tego trójkąta zawiera się w prostej o równaniu
. Przeciwprostokątna tego trójkąta zawiera się w prostej o równaniu 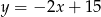 . Wyznacz współrzędne pozostałych wierzchołków trójkąta
. Wyznacz współrzędne pozostałych wierzchołków trójkąta 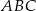 .
.
Dane są punkty 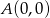 i
i 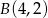 .
.
- Znajdź takie punkty
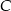 i
i 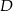 aby trójkąty
aby trójkąty 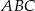 i
i 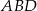 były równoboczne.
były równoboczne. - Znajdź równanie okręgu wpisanego w romb
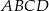 .
. - Oblicz pole figury, którą otrzymamy po usunięciu z rombu
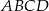 wnętrza wpisanego w niego koła.
wnętrza wpisanego w niego koła.
Różnica współczynników kierunkowych dwóch prostych jest równa różnicy odwrotności tych współczynników. Uzasadnij, że te proste są prostopadłe albo równoległe.
Dwie proste mają tę własności, że różnica współczynnika kierunkowego i jego odwrotności w przypadku każdej z tych prostych jest taka sama. Uzasadnij, że te proste są prostopadłe albo równoległe.
W równoramiennym trójkącie prostokątnym punkt 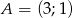 jest wierzchołkiem kąta ostrego. Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu
jest wierzchołkiem kąta ostrego. Przeciwległa do niego przyprostokątna zawiera się w prostej o równaniu 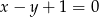 . Napisz równania prostych zawierających pozostałe boki trójkąta.
. Napisz równania prostych zawierających pozostałe boki trójkąta.

