W okrąg o środku 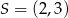 wpisano trapez w taki sposób, że jedna podstawa jest średnicą okręgu, a druga jest zawarta w prostej o równaniu
wpisano trapez w taki sposób, że jedna podstawa jest średnicą okręgu, a druga jest zawarta w prostej o równaniu 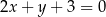 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe 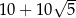 . Oblicz współrzędne tych wierzchołków trapezu, które są końcami jego krótszej podstawy.
. Oblicz współrzędne tych wierzchołków trapezu, które są końcami jego krótszej podstawy.
/Szkoła średnia/Geometria/Geometria analityczna
Rozpatrujemy wszystkie trapezy 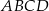 , których wierzchołki
, których wierzchołki 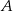 i
i 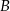 leżą na wykresie funkcji
leżą na wykresie funkcji 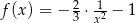 określonej dla
określonej dla 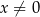 . Punkt
. Punkt 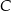 ma współrzędne
ma współrzędne 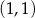 , a oś
, a oś 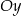 jest osią symetrii tego trapezu (zobacz rysunek).
jest osią symetrii tego trapezu (zobacz rysunek).
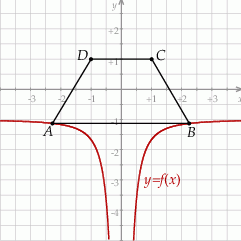
Oblicz obwód tego trapezu 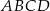 , którego pole jest najmniejsze możliwe.
, którego pole jest najmniejsze możliwe.
Wykaż, że styczne do okręgu 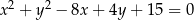 poprowadzone przez punkt
poprowadzone przez punkt 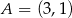 są prostopadłe.
są prostopadłe.
Środek okręgu o równaniu 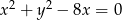 i punkt
i punkt 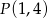 należą do prostej
należą do prostej 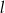 , która przecina okrąg w punktach
, która przecina okrąg w punktach 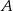 i
i 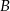 . Oblicz pole trójkąta
. Oblicz pole trójkąta 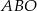 gdzie
gdzie 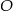 to początek układu współrzędnych.
to początek układu współrzędnych.
Podstawa 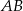 trójkąta równobocznego
trójkąta równobocznego 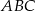 zawarta jest w prostej
zawarta jest w prostej 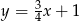 , a wierzchołek
, a wierzchołek 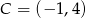 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 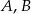 tego trójkąta.
tego trójkąta.
Wierzchołki trójkąta równobocznego 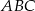 są punktami paraboli
są punktami paraboli 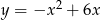 . Punkt
. Punkt 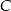 jest jej wierzchołkiem, a bok
jest jej wierzchołkiem, a bok 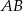 jest równoległy do osi
jest równoległy do osi 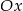 . Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta.
. Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta.
Dany jest trójkąt równoramienny 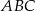 , w którym
, w którym 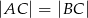 oraz
oraz 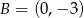 i
i 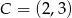 . Oś symetrii tego trójkąta ma równanie
. Oś symetrii tego trójkąta ma równanie 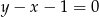 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 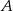 .
.
Punkty 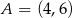 i
i 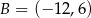 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 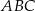 , w którym
, w którym 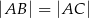 . Wysokość
. Wysokość 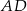 tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 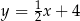 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 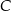 tego trójkąta.
tego trójkąta.
Punkty 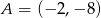 i
i 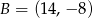 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 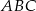 , w którym
, w którym 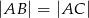 . Wysokość
. Wysokość 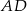 tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 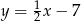 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 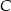 tego trójkąta.
tego trójkąta.
Punkty 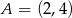 i
i 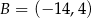 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 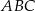 , w którym
, w którym 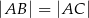 . Wysokość
. Wysokość 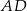 tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 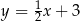 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 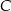 tego trójkąta.
tego trójkąta.
Dana jest prosta 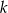 o równaniu parametrycznym
o równaniu parametrycznym 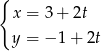 dla
dla 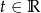 . Znajdź równanie parametryczne:
. Znajdź równanie parametryczne:
- prostej
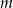 równoległej do prostej
równoległej do prostej 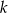 , przechodzącej przez punkt
, przechodzącej przez punkt 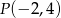 .
. - prostej
 prostopadłej do prostej
prostopadłej do prostej 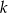 , przechodzącej przez punkt
, przechodzącej przez punkt 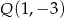 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 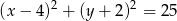 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 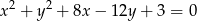 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 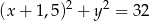 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 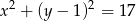 .
.
Wyznacz współrzędne środka i promień okręgu o równaniu 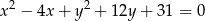 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu 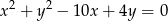 .
.
Kwadrat o wierzchołkach 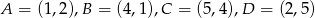 przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach
przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach 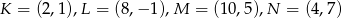 . Wyznacz środek i skalę tej jednokładności.
. Wyznacz środek i skalę tej jednokładności.
Oblicz pole pięciokąta 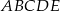 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 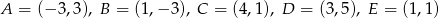 .
.
Punkty 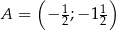 ,
, 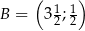 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 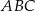 o podstawie
o podstawie 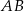 . Ramię
. Ramię 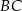 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 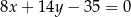 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 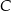 i pole tego trójkąta.
i pole tego trójkąta.
W trapezie równoramiennym 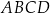 podstawa
podstawa 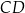 ma długość 5. Punkt
ma długość 5. Punkt 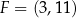 jest środkiem odcinka
jest środkiem odcinka 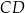 . Prosta o równaniu
. Prosta o równaniu 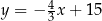 jest osią symetrii tego trapezu oraz
jest osią symetrii tego trapezu oraz 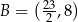 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 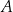 oraz pole tego trapezu.
oraz pole tego trapezu.
Dany jest punkt 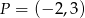 i prosta
i prosta 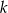 o równaniu
o równaniu 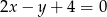 .
.
- Wyznacz równanie prostej
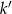 , która jest obrazem prostej
, która jest obrazem prostej 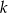 w symetrii względem punktu
w symetrii względem punktu 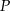 .
. - Oblicz odległość między prostymi
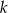 i
i 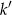 .
.
Dane są dwa wierzchołki 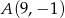 i
i 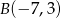 prostokąta
prostokąta 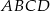 oraz punkt
oraz punkt 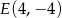 należący do boku CD.
należący do boku CD.
- Wyznacz równanie prostej zawierającej bok
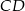 ;
; - Oblicz współrzędne wierzchołka C;
- Oblicz współrzędne punktu
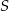 przecięcia się przekątnych tego prostokąta.
przecięcia się przekątnych tego prostokąta.
W trójkąt równoboczny 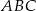 wpisano okrąg o środku w punkcie
wpisano okrąg o środku w punkcie 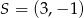 . Wiedząc, że wierzchołek
. Wiedząc, że wierzchołek 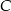 ma współrzędne
ma współrzędne 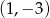 wyznacz współrzędne pozostałych wierzchołków tego trójkąta.
wyznacz współrzędne pozostałych wierzchołków tego trójkąta.
Jeden z boków kwadratu 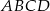 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 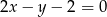 . Wierzchołek
. Wierzchołek 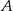 ma współrzędne
ma współrzędne 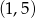 .
.
- Znajdź współrzędne pozostałych wierzchołków.
- Oblicz pole kwadratu
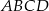 .
.
Punkt 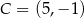 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 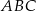 , w którym
, w którym 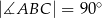 i
i 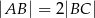 . Prosta
. Prosta 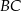 ma równanie
ma równanie 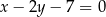 , a punkt
, a punkt 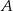 leży na prostej
leży na prostej 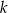 o równaniu
o równaniu 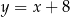 . Wyznacz współrzędne środka okręgu opisanego na trójkącie
. Wyznacz współrzędne środka okręgu opisanego na trójkącie 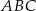 .
.
Długości wektorów 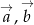 wynoszą odpowiednio 3 i 5. Ponadto znamy ich iloczyn skalarny
wynoszą odpowiednio 3 i 5. Ponadto znamy ich iloczyn skalarny 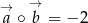 . Obliczyć iloczyn skalarny wektorów
. Obliczyć iloczyn skalarny wektorów 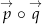 , gdzie
, gdzie 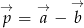 ,
,  .
.
Dwa wierzchołki prostokąta leżą na osi  , a pozostałe dwa należą do paraboli o równaniu
, a pozostałe dwa należą do paraboli o równaniu 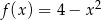 i znajdują się powyżej osi
i znajdują się powyżej osi  .
.
- Podaj wzór funkcji opisującej pole tego prostokąta w zależności od jego podstawy.
- Dla jakiej długości podstawy pole tego prostokąta jest równe 6.
- Dla jakiej długości podstawy pole tego prostokąta jest największe?

