Dla jakich liczb całkowitych dodatnich 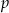 liczby
liczby 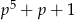 i
i 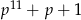 są pierwsze.
są pierwsze.
/Konkursy/Zadania/Liczby/Całkowite/Podzielność
Uzasadnij, że dla dowolnych liczb naturalnych  zachodzi równość
zachodzi równość 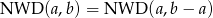 .
.
Udowodnij, że dla każdej liczby naturalnej  , liczba
, liczba 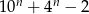 jest liczbą podzielną przez 3.
jest liczbą podzielną przez 3.
Znajdź liczbę doskonałą, która jest podzielna przez 4 i ma dokładnie 6 dzielników.
Wykaż, że jeśli  należy do zbioru liczb całkowitych, to
należy do zbioru liczb całkowitych, to 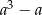 jest podzielne przez 3.
jest podzielne przez 3.
Wyznacz wszystkie liczby całkowite  , dla których liczba
, dla których liczba 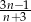 jest liczbą całkowitą.
jest liczbą całkowitą.
Udowodnij, że różnica sześcianów dwóch kolejnych liczb całkowitych nie jest liczbą podzielną przez 5.
Znajdź wszystkie liczby całkowite dodatnie  , dla których liczba
, dla których liczba 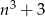 jest podzielna przez
jest podzielna przez 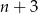 .
.
Liczby pierwsze 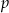 i
i 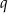 , gdzie
, gdzie 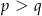 , nazywamy bliźniaczymi, jeżeli
, nazywamy bliźniaczymi, jeżeli 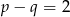 . Udowodnij, że liczby pierwsze
. Udowodnij, że liczby pierwsze 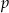 i
i 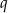 są bliźniacze wtedy i tylko wtedy, gdy
są bliźniacze wtedy i tylko wtedy, gdy 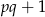 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Wykaż, że dla każdej liczby całkowitej nieparzystej  liczba
liczba 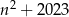 jest podzielna przez 8.
jest podzielna przez 8.
Wykaż, że jeżeli liczba  nie dzieli się przez 3, to liczba
nie dzieli się przez 3, to liczba 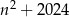 jest podzielna przez 3.
jest podzielna przez 3.
Udowodnij, że liczb pierwszych jest nieskończenie wiele.
Wykaż, że jeśli  jest liczbą nieparzystą, to liczba
jest liczbą nieparzystą, to liczba 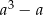 jest podzielna przez 12.
jest podzielna przez 12.
Wykaż, że dla każdej liczby naturalnej 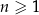 liczba
liczba 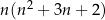 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej 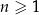 liczba
liczba 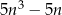 jest podzielna przez 30.
jest podzielna przez 30.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 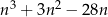 jest podzielna przez 6.
jest podzielna przez 6.
Uzasadnij, że dla każdej liczby całkowitej 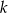 liczba
liczba 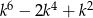 jest podzielna przez 36.
jest podzielna przez 36.
Wykaż, że jeżeli 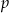 jest liczbą pierwszą większą od 3 to
jest liczbą pierwszą większą od 3 to 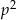 przy dzieleniu przez 24 daje resztę 1.
przy dzieleniu przez 24 daje resztę 1.
Zosia, Marysia i Ania weszły do klasy gdzie na wielkim transparencie były zapisane liczby od 1 do 7777. Zosia zakreśliła na różowo wszystkie liczby podzielne przez 3. Marysia zakreśliła na zielono wszystkie liczby podzielne przez 4. Ania zakreśliła na fioletowo wszystkie liczby podzielne przez 6. Ile liczb zostało zakreślonych dwukrotnie (bez względu na kolor)?
Dla jakich  należących do zbioru liczb naturalnych liczba
należących do zbioru liczb naturalnych liczba 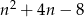 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Znajdź wszystkie liczby naturalne  takie, że liczba
takie, że liczba 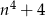 jest liczbą pierwszą.
jest liczbą pierwszą.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 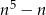 jest podzielna przez 30.
jest podzielna przez 30.
Wyznacz najmniejszą liczbę 4-cyfrową, która przy dzieleniu przez 7 daje resztę 6, a przy dzieleniu przez 6 daje resztę 5.
Dla jakich liczb całkowitych  liczba
liczba 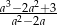 jest także liczbą całkowitą?
jest także liczbą całkowitą?

