Podaj dla jakich wartości parametru 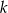 punkt przecięcia się wykresów funkcji
punkt przecięcia się wykresów funkcji 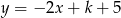 i
i 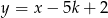 należy do II ćwiartki układu współrzędnych.
należy do II ćwiartki układu współrzędnych.
/Szkoła średnia/Równania/Układy równań/Liniowy/Z parametrem
Podaj dla jakich wartości parametru 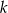 punkt przecięcia się wykresów funkcji
punkt przecięcia się wykresów funkcji 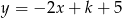 i
i 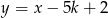 należy do półpłaszczyzny opisanej nierównością
należy do półpłaszczyzny opisanej nierównością 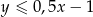 .
.
Dany jest układ równań 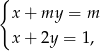 gdzie
gdzie 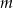 jest parametrem.
jest parametrem.
- Rozwiąż ten układ równań.
- Określ dziedzinę i naszkicuj wykres funkcji
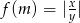 , gdzie para liczb
, gdzie para liczb 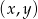 jest rozwiązaniem układu.
jest rozwiązaniem układu.
Określ liczbę rozwiązań układu równań 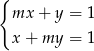 w zależności od wartości parametru
w zależności od wartości parametru 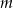 . Dla tych wartości
. Dla tych wartości 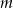 , dla których istnieją rozwiązania, rozwiąż ten układ.
, dla których istnieją rozwiązania, rozwiąż ten układ.
Dany jest układ równań
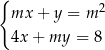
z niewiadomymi  i
i 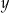 oraz parametrem
oraz parametrem 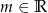 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 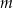 , dla których układ jest oznaczony, a para liczb
, dla których układ jest oznaczony, a para liczb 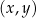 będąca rozwiązaniem układu spełnia warunek
będąca rozwiązaniem układu spełnia warunek 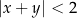 .
.
Dla jakich wartości parametru 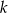 wśród rozwiązań układu równań:
wśród rozwiązań układu równań:
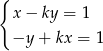
jest para liczb 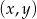 spełniających warunek:
spełniających warunek: 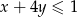 ?
?
Dla jakich współczynników  i
i  układ
układ 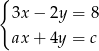
- ma nieskończenie wiele rozwiązań;
- jest sprzeczny?
W kartezjańskim układzie współrzędnych 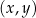 proste o równaniach
proste o równaniach 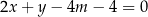 oraz
oraz 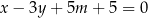 przecinają się w punkcie
przecinają się w punkcie 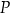 o współrzędnych
o współrzędnych 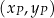 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 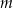 , dla których współrzędne punktu
, dla których współrzędne punktu 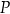 spełniają warunki:
spełniają warunki:
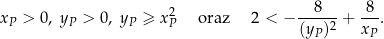
Dla jakich wartości parametru 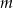 rozwiązaniem układu
rozwiązaniem układu 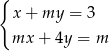 jest para liczb
jest para liczb 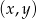 spełniająca nierówność
spełniająca nierówność 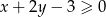 ?
?
Wyznacz te wartości parametru 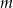 , dla których rozwiązaniem układu równań
, dla których rozwiązaniem układu równań 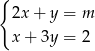 jest para liczb różnych znaków.
jest para liczb różnych znaków.
Dla jakich wartości parametru  układ równań
układ równań 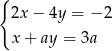 ma rozwiązanie będące parą liczb o różnych znakach?
ma rozwiązanie będące parą liczb o różnych znakach?
Dla jakich wartości parametru 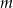 rozwiązaniem układu równań
rozwiązaniem układu równań 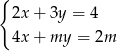 jest para liczb nieujemnych?
jest para liczb nieujemnych?
Dla jakich wartości parametru 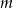 rozwiązaniem układu równań
rozwiązaniem układu równań 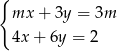 jest para liczb nieujemnych?
jest para liczb nieujemnych?
Dany jest układ równań: 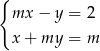 .
.
Dla każdej wartości parametru 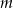 wyznacz parę liczb
wyznacz parę liczb 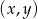 , która jest rozwiązaniem tego układu równań. Wyznacz najmniejszą wartość sumy
, która jest rozwiązaniem tego układu równań. Wyznacz najmniejszą wartość sumy 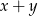 dla
dla 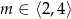 .
.
Wyznacz takie liczby  i
i 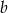 , dla których układ równań
, dla których układ równań 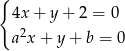 jest sprzeczny, zaś układ równań
jest sprzeczny, zaś układ równań 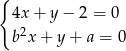 ma nieskończenie wiele rozwiązań.
ma nieskończenie wiele rozwiązań.
Dla jakich wartości parametru 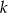 rozwiązanie układu równań
rozwiązanie układu równań 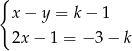 spełnia warunek
spełnia warunek 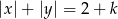 ?
?
Podaj te wartości  , przy których dla każdego
, przy których dla każdego 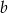 istnieje takie
istnieje takie  , że układ równań:
, że układ równań:
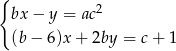
ma zawsze przynajmniej jedno rozwiązanie.
Wyznacz te wartości parametru 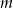 , dla których rozwiązaniem układu równań
, dla których rozwiązaniem układu równań 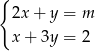 jest para liczb dodatnich.
jest para liczb dodatnich.
Podaj dla jakich wartości parametru 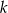 punkt przecięcia się wykresów funkcji
punkt przecięcia się wykresów funkcji 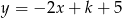 i
i 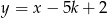 należy do koła o środku
należy do koła o środku 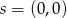 i promieniu
i promieniu 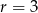 .
.

