W wazonie stoi 12 czerwonych i 8 żółtych róż. Pani Krystyna wyjęła losowo dwie róże z wazonu. Oblicz prawdopodobieństwo, że wśród wybranych kwiatów jest przynajmniej jedna róża żółta.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Różne
W garderobie pani Joanny wiszą 3 żakiety: biały, zielony i granatowy oraz 4 spódnice: czarna, biała, granatowa i szara. Oblicz prawdopodobieństwo zdarzenia, że wybierając losowo jeden żakiet i jedną spódnicę, pani Joanna skompletuje strój w jednym kolorze.
Łukasz w sposób losowy ustawia na jednej półce regału pewną liczbę książek. Wśród tych książek są trzy książki w języku angielskim, a wszystkie pozostałe są w języku polskim. Prawdopodobieństwo zdarzenia polegającego na tym, że trzy książki w języku angielskim znajdą się obok siebie jest równe 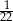 . Oblicz, ile książek w języku polskim zostało ustawionych na tej półce.
. Oblicz, ile książek w języku polskim zostało ustawionych na tej półce.
Strzelając do tarczy pewien strzelec uzyskuje co najmniej 9 punktów z prawdopodobieństwem 0,5, a co najwyżej 9 punktów z prawdopodobieństwem 0,7. Oblicz prawdopodobieństwo, że ten strzelec uzyska dokładnie 9 punktów.
Rzucamy sześcienną kostką i monetą. Jakie jest prawdopodobieństwo, że na monecie wypadnie reszka, a na kostce nie więcej niż 4 oczka.
Zakupiono 16 biletów do teatru, w tym 10 biletów na miejsca od 1. do 10. w pierwszym rzędzie i 6 biletów na miejsca od 11. do 16. w szesnastym rzędzie. Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że 2 wylosowane bilety, spośród szesnastu, będą biletami na sąsiadujące miejsca?
Mamy 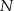 pałek o jednakowej długości. Każdą z nich łamiemy na 2 części: długą i krótką.
pałek o jednakowej długości. Każdą z nich łamiemy na 2 części: długą i krótką. 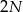 części połączono losowo w
części połączono losowo w 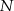 par, z których utworzono nowe pałki. Wyznacz prawdopodobieństwo tego, że:
par, z których utworzono nowe pałki. Wyznacz prawdopodobieństwo tego, że:
- części zostaną połączone tak, jak przed złamaniem;
- wszystkie długie części będą połączone z krótkimi.
Paulina ma w szafie 20 bluzek w kilku kolorach. W tabelce przedstawiono, jaki procent bluzek stanowią bluzki w danym kolorach
| Kolor bluzki | % |
| czerwony | 15 |
| niebieski | 70 |
| czarny | 5 |
| biały | 10 |
Oblicz prawdopodobieństwo, że wybrana losowo bluzka jest niebieska.
Ze zbioru 26 liter alfabetu łacińskiego 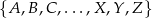 losujemy bez zwracania trzy razy jedną literę. Oblicz prawdopodobieństwo tego, że wśród wylosowanych liter znalazła się przynajmniej jedna z liter
losujemy bez zwracania trzy razy jedną literę. Oblicz prawdopodobieństwo tego, że wśród wylosowanych liter znalazła się przynajmniej jedna z liter 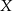 ,
, 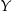 lub
lub 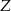 .
.
Rzucamy jednocześnie kostką i sześcioma symetrycznymi monetami. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, liczba otrzymanych oczek na kostce jest równa łącznej liczbie otrzymanych orłów na monetach.
Na trzy półki kładziemy losowo 5 książek. Jakie jest prawdopodobieństwo tego, że jedna (i tylko jedna) z półek zostanie pusta?.
Mamy 10 książek, wśród których są książki 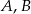 i
i 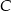 . Ustawiamy je losowo na pustej półce. Oblicz prawdopodobieństwo, że książki
. Ustawiamy je losowo na pustej półce. Oblicz prawdopodobieństwo, że książki 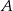 i
i 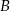 będą stały obok siebie w dowolnym porządku, natomiast
będą stały obok siebie w dowolnym porządku, natomiast 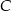 nie będzie sąsiadować z żadną z nich.
nie będzie sąsiadować z żadną z nich.
Po przypadkowo wybranych równoległych do siebie torach czterotorowej linii kolejowej jadą naprzeciw siebie 2 drezyny. Oblicz prawdopodobieństwo ich zderzenia.
Z dworca prowadzą dwa wyjścia: wyjście 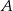 na przystanek autobusowy oraz
na przystanek autobusowy oraz 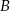 na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem
na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem 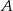 z prawdopodobieństwem 30%, a wyjściem
z prawdopodobieństwem 30%, a wyjściem 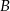 z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że wszyscy wybiorą wyjście
z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że wszyscy wybiorą wyjście 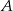 .
.
Z dworca prowadzą dwa wyjścia: wyjście 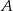 na przystanek autobusowy oraz
na przystanek autobusowy oraz 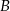 na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem
na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem 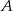 z prawdopodobieństwem 30%, a wyjściem
z prawdopodobieństwem 30%, a wyjściem 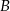 z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że tylko dwaj z nich wybiorą to samo wyjście.
z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że tylko dwaj z nich wybiorą to samo wyjście.
Z dworca prowadzą dwa wyjścia: wyjście 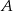 na przystanek autobusowy oraz
na przystanek autobusowy oraz 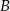 na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem
na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem 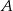 z prawdopodobieństwem 30%, a wyjściem
z prawdopodobieństwem 30%, a wyjściem 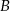 z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że wszyscy wybiorą to samo wyjście.
z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że wszyscy wybiorą to samo wyjście.
Z dworca prowadzą dwa wyjścia: wyjście 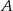 na przystanek autobusowy oraz
na przystanek autobusowy oraz 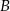 na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem
na postój taksówek. Stwierdzono, że pasażer wychodzi wyjściem 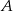 z prawdopodobieństwem 30%, a wyjściem
z prawdopodobieństwem 30%, a wyjściem 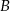 z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że jeden wybierze wyjście
z prawdopodobieństwem 70%. Losowo wybrano trzech pasażerów. Oblicz prawdopodobieństwo tego, że jeden wybierze wyjście 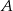 , a pozostali dwaj, wyjście
, a pozostali dwaj, wyjście 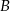 .
.
Dany jest wielomian 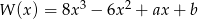 . Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
. Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
Piotrek ma 100 płyt CD z muzyką poważną. Codziennie słucha jednej płyty i odstawia ją na miejsce. Płyty wybiera w sposób losowy. Oblicz prawdopodobieństwo, że w ciągu pięciu kolejnych dni będzie słuchał codziennie tej samej płyty.
Wybieramy losowo 2 kostki z tabliczki czekolady przedstawionej na poniższym rysunku.

Oblicz prawdopodobieństwo tego, że wybrane dwie kostki są sąsiednie (tzn. mają wspólną krawędź).

